1.1.4: Ceros e Intercepciones
- Page ID
- 109000
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ceros e Intercepciones de Funciones
Una intercepción en matemáticas es donde una función cruza el eje x o y. ¿Cuáles son las intercepciones de esta función?
[Figura1]Intercepciones X e Y
El primer tipo de intercepción que puede haber aprendido es la intersección y cuando aprendió la forma de intercepción de pendiente de una línea: y=mx+b. Una intercepción y es el punto único donde una función cruza el eje y. Se puede encontrar algebraicamente estableciendo x=0 y resolviendo para y.
Las intercepciones x son donde las funciones cruzan el eje x y donde la altura de la función es cero. También se les llama raíces, soluciones y ceros de una función. Se encuentran algebraicamente estableciendo y=0 y resolviendo para x. Vea los videos a continuación para practicar:
Ejemplos
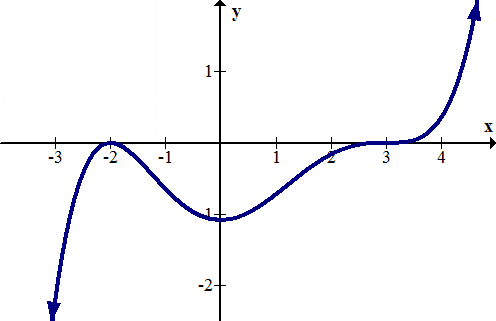
Anteriormente, se le preguntó cuáles son las intercepciones de la gráfica a continuación.
[Figura2]Solución
Gráficamente la función tiene ceros en -2 y 3 con una intersección y en aproximadamente -1.1.
Nota: Para que una función pase la prueba de línea vertical, solo debe tener una intercepción y, pero puede tener múltiples intercepciones x.
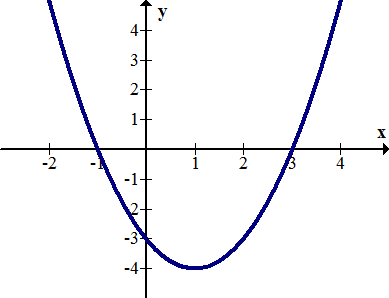
¿Cuáles son los ceros y las intercepciones y de la parábola y=x 2 −2x−3?
Usando una gráfica:
[Figura3]Solución
Los ceros están en (-1, 0) y (3, 0). La intercepción y está en (0, -3).
Usando Álgebra:
Sustituye 0 por y para encontrar ceros.
0=x 2 −2x−3 =( x−3) (x+1)
y=0, x=3, −1
Sustituye 0 por x para encontrar la intersección y.
y= (0) 2 −2 (0) −3=−3
x=0, y=−3
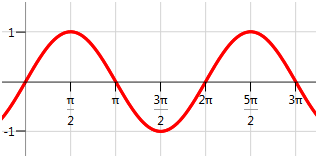
Identificar los ceros e intercepciones y para la función sinusoidal.
[Figura4]Solución
La intercepción y es (0, 0). Hay cuatro ceros visibles en esta parte de la gráfica. Una cosa que sabes de la gráfica sinusoidal es que es periódica y se repite para siempre en ambas direcciones. Para capturar cada intercepción x, debes identificar un patrón en lugar de intentar escribir cada una de ellas.
Las intercepciones x visibles son 0, π,2π,3π. El patrón es que hay una intercepción x cada múltiplo de π incluyendo múltiplos negativos. Para describir todos estos valores debes escribir:
Las intercepciones x son ±nπ donde n es un entero {0, ±1, ±2,...}.
Identificar las intercepciones y ceros de la función:\(\ f(x)=\frac{1}{100}(x-3)^{3}(x+2)^{2}\)
Solución
Para encontrar la intersección y, sustituya 0 por x:
\(\ y=\frac{1}{100}(0-3)^{3}(0+2)^{2}=\frac{1}{100}(-27)(4)=-\frac{108}{100}=-1.08\)
Para encontrar las intercepciones x, sustituya 0 por y:
\(\ 0=\frac{1}{100}(x-3)^{3}(x+2)^{2}\)
x=3, −2
Así, la intersección y es (0, -1.08) y las intercepciones x son (3, 0) y (-2, 0).
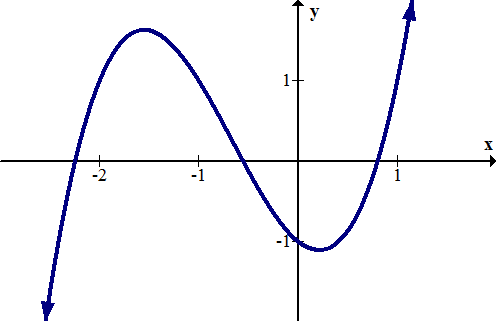
Determinar gráficamente las intercepciones de la siguiente función.
[Figura5]Solución
La intersección y es aproximadamente (0, -1). Las intercepciones x son aproximadamente (-2.3, 0), (-0.4, 0) y (0.7, 0). Al encontrar valores gráficamente, las respuestas son siempre aproximadas. Las respuestas exactas deben encontrarse analíticamente.
Revisar
1. Determine los ceros y la intersección y de la siguiente función usando álgebra:
f (x) = (x+1) 3 (x−4)
2. Determine las raíces y la intersección y de la siguiente función usando álgebra o una gráfica:
g (x) =x 4 −2x 3 −7x 2 +20x−12
3. Determine gráficamente las intercepciones de la siguiente función:
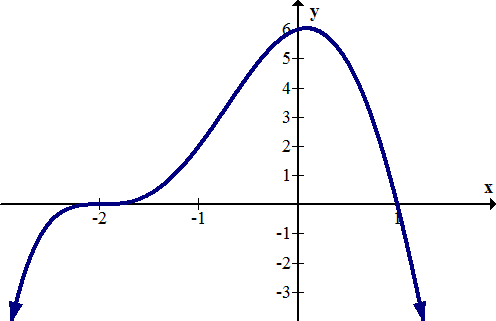[Figura6]Encuentra las intercepciones para cada una de las siguientes funciones.
4. y=x 2
5. y=x 3
6. y=ln (x)
7. y=\(\ \frac{1}{x}\)
8. y=e x
9. y=\(\ \sqrt{x}\)
10. ¿Hay alguna función sin una intercepción en Y? Explique.
11. ¿Hay alguna función sin una intercepción x? Explique.
12. Explique por qué tiene sentido que una intercepción x de una función también se llame “cero” de la función.
Determinar las intercepciones de las siguientes funciones utilizando álgebra o una gráfica.
13. h (x) =x 3 −6x 2 +3x+10
14. j (x) =x 2 −6x−7
15. k (x) =4x 4 −20x 3 −3x 2 +14x+5
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.8.
El vocabulario
| Término | Definición |
|---|---|
| Interceptar | Las intercepciones de una curva son las ubicaciones donde la curva interseca los ejes x e y. Una intersección x es un punto en el que la curva cruza el eje x. Una intersección y es un punto en el que la curva cruza el eje y. |
| Intercepta | Las intercepciones de una curva son las ubicaciones donde la curva interseca los ejes x e y. Una intersección x es un punto en el que la curva cruza el eje x. Una intersección y es un punto en el que la curva cruza el eje y. |
| Raíces | Las raíces de una función son los valores de x que hacen y igual a cero. |
| Prueba de línea vertical | La prueba de línea vertical dice que si una línea vertical dibujada en cualquier parte a través de la gráfica de una relación interseca la relación en más de una ubicación, entonces la relación no es una función. |
| Ceros | Los ceros de una función f (x) son los valores de x que hacen que f (x) sea igual a cero. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 2]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 3]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 4]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 5]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 6]
Crédito: Fundación CK-12
Licencia: CC BY-SA