1.2.2: Funciones discretas y continuas
- Page ID
- 109043
Continuidad y Discontinuidad
La continuidad es una propiedad de las funciones que se pueden dibujar sin levantar el lápiz. Algunas funciones, como las funciones recíprocas, tienen dos partes distintas que están desconectadas. Las funciones que están desconectadas son discontinuas. ¿Cuáles son las tres formas en que las funciones pueden ser discontinuas y cómo surgen?
Continuidad y Discontinuidad de Funciones
Las funciones que se pueden dibujar sin levantar el lápiz se denominan funciones continuas. Definirás continuo de una manera matemáticamente más rigurosa después de estudiar los límites.
Existen tres tipos de discontinuidades: Removible, Salto e Infinito.
Discontinuidades removibles
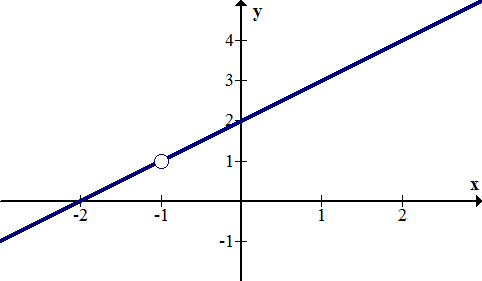
Las discontinuidades removibles ocurren cuando una función racional tiene un factor con una x que existe tanto en el numerador como en el denominador. Las discontinuidades removibles se muestran en una gráfica mediante un círculo hueco que también se conoce como agujero. A continuación se muestra la gráfica para\(\ f(x)=\frac{(x+2)(x+1)}{x+1}\). Observe que se ve igual que y=x+2 excepto por el agujero en x=−1. Al graficar la función, debe cancelar el factor removible, graficar como de costumbre y luego insertar un agujero en el punto apropiado al final. Hay un agujero en x=−1 porque cuando\(\ x=-1, f(x)=\frac{0}{0}\)
 [Figura1]
[Figura1]Las discontinuidades removibles se pueden “rellenar” si se hace de la función una función por partes y se define una parte de la función en el punto donde se encuentra el agujero. En el ejemplo anterior, para hacer f (x) continuo podrías redefinirlo como:
\ (\ f (x) =\ left\ {\ begin {array} {ll}
\ frac {(x+2) (x+1)} {x+1}, & x\ neq-1\\
1, & x=-1
\ end {array}\ right.\)
Discontinuidades de salto
Las discontinuidades de salto ocurren cuando una función tiene dos extremos que no se encuentran aunque el agujero esté lleno. Para satisfacer la prueba de línea vertical y asegurarse de que la gráfica sea realmente la de una función, solo se puede llenar uno de los puntos finales. A continuación se muestra un ejemplo de una función con una discontinuidad de salto.
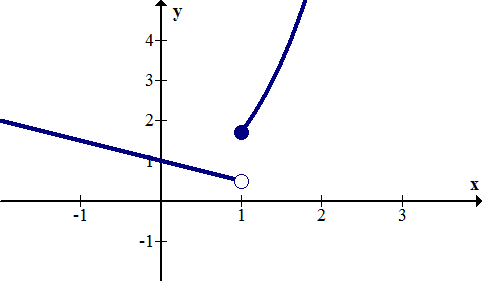 [Figura2]
[Figura2]Discontinuidades infinitas
Las discontinuidades finitas ocurren cuando una función tiene una asíntota vertical en uno o ambos lados. Esto se muestra en la gráfica de la función a continuación en x=1.
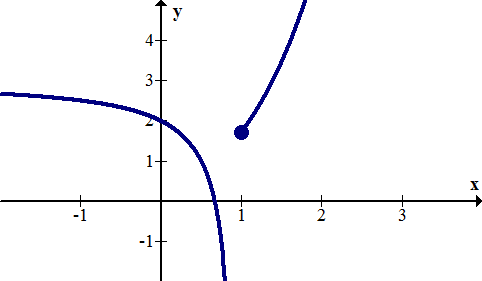 [Figura3]
[Figura3]Ejemplos
Solución
Anteriormente se le preguntó cómo las funciones pueden ser discontinuas. Hay tres formas en que las funciones pueden ser discontinuas. Cuando una función racional tiene una asíntota vertical como resultado de que el denominador es igual a cero en algún momento, tendrá una discontinuidad infinita en ese punto. Cuando el numerador y denominador de una función racional tengan uno o más de los mismos factores, habrá discontinuidades removibles correspondientes a cada uno de estos factores. Por último, cuando las diferentes partes de una función por partes no “coinciden”, habrá una discontinuidad de salto.
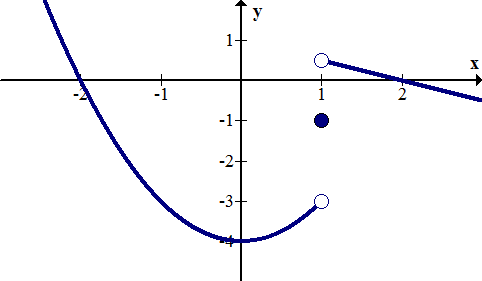
Identificar gráficamente la discontinuidad de la función por partes.
\ (\ f (x) =\ izquierda\ {\ begin {array} {ll}
x^ {2} -4 & x<1\\
-1 & x=1\\
-\ frac {1} {2} x+1 & x>1
\ end {array}\ derecha.\)
 [Figura4]
[Figura4]Solución
Hay una discontinuidad de salto en x=1. La función por partes describe una función en tres partes; una parábola a la izquierda, un solo punto en el medio y una línea a la derecha.
Describir la continuidad o discontinuidad de la función\(\ f(x)=\sin \left(\frac{1}{x}\right)\)
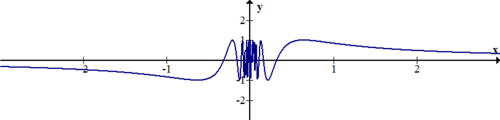 [Figura5]
[Figura5]Solución
La función parece oscilar infinitamente a medida que x se acerca a cero. Una cosa que la gráfica no logra mostrar es que 0 claramente no está en el dominio. El gráfico no dispara al infinito, ni tiene un simple agujero o discontinuidad de salto. Se requiere de Cálculo y Análisis Real para exponer con mayor precisión lo que está sucediendo.
Describa las discontinuidades de la función a continuación.
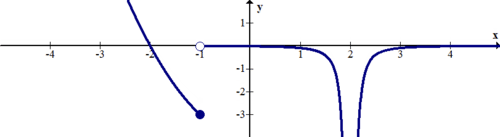 [Figura6]
[Figura6]Solución
Hay una discontinuidad de salto en x=−1 y una discontinuidad infinita en x=2.
Describa las discontinuidades de la función a continuación.
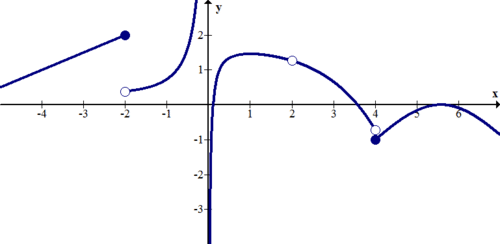 [Figura7]
[Figura7]Solución
Hay discontinuidades de salto en x=−2 y x=4. Hay una discontinuidad removible en x=2. Hay una discontinuidad infinita en x=0.
Revisar
Describa las discontinuidades en las siguientes funciones:
1. y=x
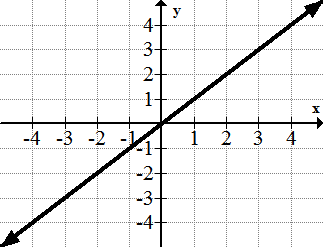 [Figura8]
[Figura8]2. y=x 2
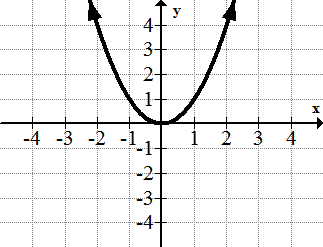 [Figura9]
[Figura9]3. y=x 3
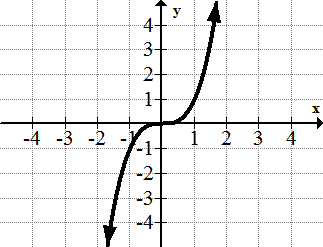 [Figura10]
[Figura10]4. \(\ y=\sqrt{x}\)
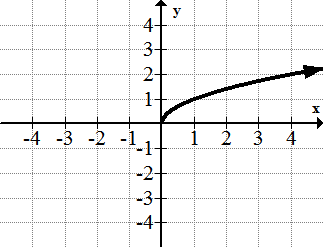 [Figura11]
[Figura11]5. \(\ y=\frac{1}{x}\)
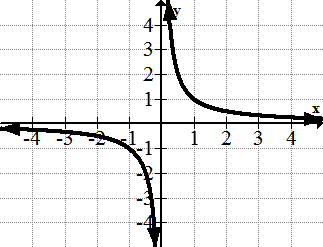 [Figura12]
[Figura12]6. y=e x
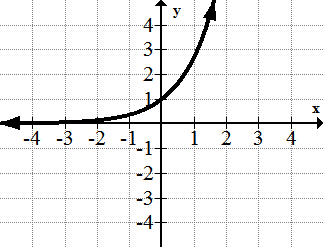 [Figura13]
[Figura13]7. y=ln (x)
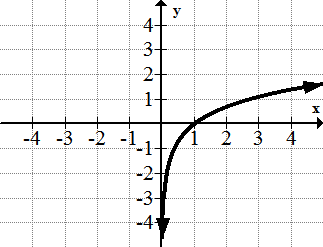 [Figura14]
[Figura14]8. \(\ y=\frac{1}{1+e^{-x}}\)
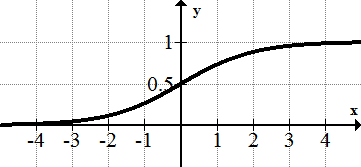 [Figura15]
[Figura15]9.
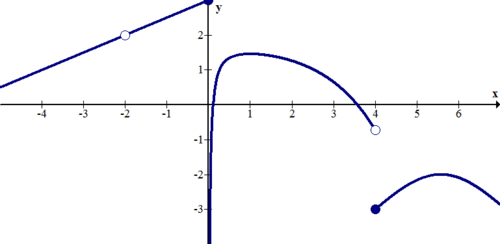 [Figura16]
[Figura16]10.
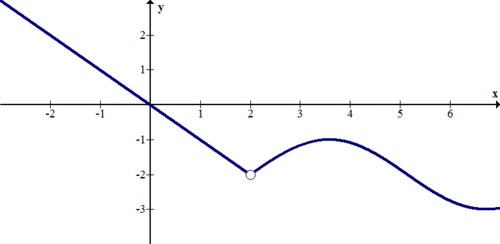 [Figura17]
[Figura17]11.
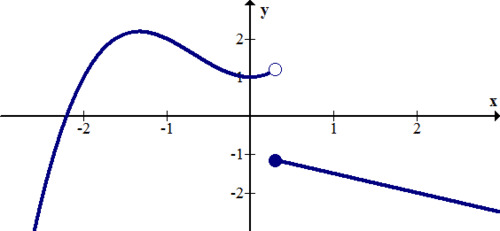 [Figura18]
[Figura18]12. f (x) tiene una discontinuidad de salto en x=3, una discontinuidad removible en x=5 y otra discontinuidad de salto en x=6. Dibuja una imagen de una gráfica que podría ser f (x).
13. g (x) tiene una discontinuidad de salto en x=−2, una discontinuidad infinita en x=1 y otra discontinuidad de salto en x=3. Dibuja una imagen de una gráfica que podría ser g (x).
14. h (x) tiene una discontinuidad removible en x=−4, una discontinuidad de salto en x=1 y otra discontinuidad de salto en x=7. Dibuja una imagen de una gráfica que podría ser h (x).
15. j (x) tiene una discontinuidad infinita en x=0, una discontinuidad removible en x=1 y una discontinuidad de salto en x=4. Dibuja una imagen de una gráfica que podría ser j (x).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.10.
El vocabulario
| Término | Definición |
|---|---|
| Continuo | La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido. |
| discontinuidades | Los puntos de discontinuidad para una función son los valores de entrada de la función donde la función es discontinua. |
| Discreta | Se dice que una relación es discreta si hay un número finito de puntos de datos en su gráfica. Las gráficas de relaciones discretas aparecen como puntos. |
| Función | Una función es una relación donde solo hay una salida por cada entrada. En otras palabras, por cada valor de x, solo hay un valor para y. |
| Discontinuidades infinitas | Las discontinuidades infinitas ocurren cuando una función tiene una asíntota vertical en uno o ambos lados. Esto sucederá cuando un factor en el denominador de la función sea cero. |
| Discontinuidad infinita | Las discontinuidades infinitas ocurren cuando una función tiene una asíntota vertical en uno o ambos lados. Esto sucederá cuando un factor en el denominador de la función sea cero. |
| intervalo | Un intervalo es una parte específica y limitada de una función. |
| Discontinuidades de salto | Las funciones inversas son funciones que se 'deshacen' entre sí. Formalmente f (x) y g (x) son funciones inversas si f (g (x)) =g (f (x)) =x. |
| Discontinuidades removibles | Las discontinuidades removibles también se conocen como agujeros. Ocurren cuando los factores pueden ser cancelados algebraicamente a partir de funciones racionales. |
| Discontinuidad removible | Las discontinuidades removibles también se conocen como agujeros. Ocurren cuando los factores pueden ser cancelados algebraicamente a partir de funciones racionales. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 2]
Crédito: Fundación CK-12
Fuente: https://www.flickr.com/photos/jhaymesisvip/6497720753/
Licencia: CC BY-SA - [Figura 3]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 4]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 5]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 6]
Crédito: Fundación CK-12
Fuente: https://www.flickr.com/photos/jhaymesisvip/6497720753/
Licencia: CC BY-SA - [Figura 7]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 8]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 9]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 10]
Crédito: Fundación CK-12
Fuente: http://classconnection.s3.amazonaws.com/753/flashcards/449753/png/screen_shot_2011-09-21_at_8.07.32_pm1316650094429.png
Licencia: CC BY-SA - [Figura 11]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 12]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 13]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 14]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 15]
Crédito: Fundación CK-12; Paula Evans; Rob Young
Fuente: https://www.flickr.com/photos/rob-young/1149735229/; https://commons.wikimedia.org/wiki/File:Will_%26_Grace_ Apartment_Building_ (1149735229) .jpg
Licencia: CC BY-SA; CC BY-NC-SA - [Figura 16]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 17]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 18]
Crédito: Fundación CK-12
Licencia: CC BY-SA

