1.4.1: Familias de funciones de valores lineales y absolutos

Última actualización
Guardar como PDF

Page ID: 109027

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Familias de funciones de valores lineales y absolutos

El martes, la clase de matemáticas del señor Varner se archivó en la sala, y se quedó boquiabierto ante el mensaje en la pizarra: “¡El primer alumno en sumar todos los números entre 1 y 100 gana cuatro entradas de cine gratis para el teatro el próximo viernes!” Todos agarraron un lápiz y empezaron a agregar: 1 + 2 + 3 + 4 + 5... Nadie estaba más allá de los 20 cuando Brian entró, tarde como de costumbre, miró la pizarra blanca durante unos 15 segs, y escribió: “5050" en la parte inferior. El sorprendido señor Varner le entregó los boletos a Brian y le dijo que tomara su asiento.

¿Cómo se le ocurrió la respuesta tan rápido?

Familias de funciones de valores lineales y absolutos

En este Concepto examinaremos varias familias de funciones. Una familia de funciones es un conjunto de funciones cuyas ecuaciones tienen una forma similar. El padre de la familia es la ecuación en la familia con la forma más simple. Por ejemplo, y = x ² es padre de otras funciones, como y = 2x ² - 5x + 3.

Familia de funciones lineales

Una ecuación es un miembro de la familia de funciones lineales si no contiene potencias\(\ x\) mayores que

1. Por ejemplo,\(\ y=2x\) y\(\ y=2\) son ecuaciones lineales, mientras que\(\ y=x^{2}\) y\(\ y=\frac{1}{x}\) son no lineales.

Las ecuaciones lineales se denominan lineales porque sus gráficas forman líneas rectas. Como recordará de sus estudios anteriores de álgebra, podemos describir cualquier línea por su tasa promedio de cambio, o pendiente, y su intercepción y. (De hecho, ¡es la pendiente constante de una línea lo que la convierte en una línea!) Estos aspectos de una línea son más fáciles de identificar si la ecuación de la línea está escrita en forma de pendiente-intercepción, o y = mx + b. La pendiente de la línea es igual al coeficiente m, y la intercepción y de la línea es el punto (0, b).

Tenga en cuenta que una línea puede ser miembro de una familia como la familia de “funciones lineales”, y también un miembro de una subfamilia de funciones lineales con la misma pendiente. Las gráficas de esta subfamilia serán un conjunto de líneas paralelas. Una subfamilia particular de funciones lineales es la subfamilia de funciones constantes. La línea x = 5 es una función constante, ya que los valores de la función son constantes, o inmutables. La “subfamilia” de funciones constantes de funciones lineales está compuesta por funciones cuyas gráficas son líneas horizontales.

Familia de funciones de valor absoluto

Consideremos primero al padre de familia: y = | x |. Debido a que el valor absoluto de un número es la distancia de ese número desde cero, todos los valores de función de una función de valor absoluto no serán negativos. Si x = 0, entonces y = |0| = 0. Si x es positivo, entonces el valor de la función es igual a x. Por ejemplo, la gráfica contiene los puntos (1, 1), (2, 2), (3, 3), etc. Sin embargo, cuando x es negativo, el valor de la función será el opuesto al número. Por ejemplo, la gráfica contiene los puntos (-1, 1), (-2, 2), (-3, 3), etc. Como se puede ver en la gráfica de abajo, la función de valor absoluto forma una forma de “V”.

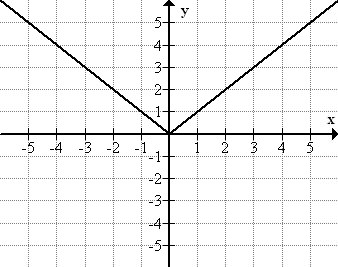
F-d_96a4c366511e0b5bbb4f9de7d2f879495e8618363bccb1ae41203f95+image_tiny+image_tiny.jpg

Hay dos cosas importantes a tener en cuenta sobre la gráfica de este tipo de funciones. Primero, la gráfica de valores absolutos tiene un vértice (un punto más alto o más bajo) y una línea de simetría (una línea que divide la función en 'mitades' iguales y opuestas). Por ejemplo, la gráfica de y = | x | tiene su vértice en (0, 0) y es simétrica a través del eje y. Segundo, tenga en cuenta que la gráfica no es curva, sino compuesta por dos porciones rectas. Toda gráfica de valores absolutos tomará esta forma, siempre y cuando la expresión dentro del valor absoluto sea lineal.

Funciones definidas por piezas

Consideremos nuevamente la función y = | x |. Para valores x positivos, la gráfica se asemeja a la función de identidad y = x. Para valores de x negativos, la gráfica se asemeja a la función y = - x. Podemos expresar esta relación definiendo la función de valor absoluto en dos partes:

\ (\ f (x) =\ left\ {\ begin {array} {l}
-x, x<0\\
x, x\ geq 0
\ end {array}\ right.\)

Podemos leer esta notación como: los valores de la función son iguales a - x si x es negativo. Los valores de la función son iguales a x si x es 0 o positivo.

Una función definida por partes no tiene que representar una función que ya se pueda escribir como una sola ecuación, como la función de valor absoluto. Por ejemplo, una “pieza” puede ser de una familia de funciones, mientras que otra pieza es de una familia de funciones diferente.

Ejemplos

Ejemplo 1

Solución

Anteriormente, se le dio un problema sobre el regalo de clases de matemáticas del señor Varner.

Escribió el siguiente mensaje en la pizarra: “¡El primer alumno en sumar todos los números entre 1 y 100 gana cuatro entradas de cine gratis para el teatro el próximo viernes!” Todos agarraron un lápiz y empezaron a agregar: 1 + 2 + 3 + 4 + 5... Nadie estaba más allá de los 20 cuando Brian entró, miró la pizarra blanca durante unos 15 segs y escribió: “5050" en la parte inferior. El señor Varner le entregó los boletos a Brian y le dijo que tomara su asiento. ¿Cómo se le ocurrió la respuesta tan rápido?

Brian reconoció que no necesitaba sumar cada uno de los números individualmente, solo los pares: 100 + 0 = 100, también lo hace 99 + 1, y 98 + 2, y así sucesivamente. Ya que hay 50 pares de 100, eso suma hasta 5000. El único número sin par es 50, por lo que se suma al total: 5050.

Las familias de funciones representan este mismo tipo de ahorro de tiempo. Al reconocer bits comunes de información y combinarlos de diferentes maneras, podemos 'automatizar' algunos procesos que parecen muy complejos.

Ejemplo 2

Identificar la pendiente y la intercepción y de cada línea.

\(\ y=\frac{2}{3} x-1\)
\(\ y=5\)
\(\ x=−2\)
\(\ y=\frac{2}{3} x+3\)

Solución

Esta línea tiene pendiente (2/3) y la intercepción y es el punto (0, -1).
Esta es una línea horizontal. La pendiente es 0, y la intercepción y es (0,5).
Esta es una línea vertical. La pendiente es indefinida, y la línea no cruza el eje y. (¡Tenga en cuenta que esta línea no es una función!)
La pendiente de esta línea es 2/3, y la intercepción y es el punto (0, 3).

Ejemplo 3

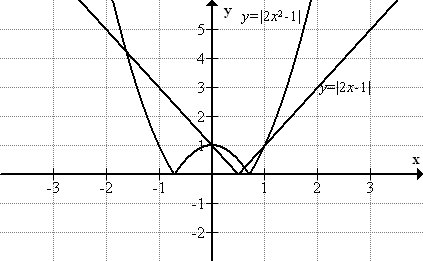
Grafica lo siguiente:\(\ y=|2 x-1| \text { and } y=\left|2 x^{2}-1\right|\).

Solución

La gráfica de\(\ y=|2 x-1|\) hace una forma de “V”, al igual que\(\ y=|x|\).

La función dentro del valor absoluto,\(\ 2x+1\), es lineal, por lo que la gráfica se compone de líneas rectas.

El gráfico de\(\ y=\left|2 x^{2}-1\right|\) es curvo, y no tiene un solo vértice, sino dos “cúspides”.

La función dentro del valor absoluto NO es lineal, por lo tanto la gráfica contiene curvas.

f-d_c809891db6bfb54ca992c80b570df5f85fda82eded758e8b560187d8+image_tiny+image_tiny.jpg

Ejemplo 4

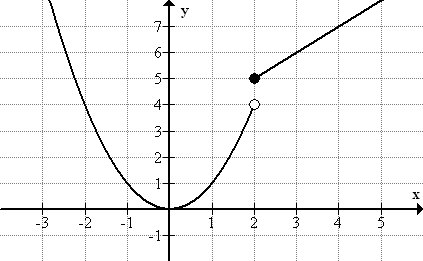
Croquis de una gráfica de la función

\ (\ f (x) =\ left\ {\ begin {array} {l}
x^ {2}, x<2\\
x+3, x\ geq 2
\ end {array}\ right.\)

Solución

f-d_0a4e522a0c41703ecec2cf2da91fb72a1e2e3a1514dd9660c8c0f25f+image_tiny+image_tiny.jpg

Es importante señalar que las piezas de una función definida por piezas pueden o no encontrarse. Por ejemplo, en la gráfica de f (x) anterior, el valor de la función es 4 a x = -2, pero la pieza de la gráfica que se define por x + 3 se encabeza al valor y de 1. Por lo tanto las dos piezas no se encuentran.

Ejemplo 5

Encuentra las intercepciones x de la función\(\ f(x)=8|x-7|-64\).

Solución

Para encontrar las intercepciones x, establezca f (x) igual a 0 y resuelva para x:

0=8|x−7|−64

64=8|x−7|

8=|x−7|

8= (x−7) u 8=− (x−7)

15=x o −1=x

* las intercepciones x son 15 y -1

Ejemplo 6

¿Cuál es la gráfica de y=|x|? ¿Cómo se relaciona esa gráfica con la gráfica de y=a|x−h|+k? ¿Qué sucede con la gráfica de y=|x| cuando la ecuación cambia a y=|x|−5?

Solución

A continuación se muestra la gráfica de y=|x|. Puede usar una herramienta gráfica o trazar puntos, señalando que cada x positiva tiene una y coincidente, y cada x negativa coincide con su equivalente positivo como y. y=|x| es el ejemplo más simple de un graph en la familia de funciones de valor absoluto, de la cual y=a|x−h|+k es el padre. Los cambios a a, h y k desplazan la gráfica de y=|x| de diferentes maneras.

f-d_bdbe040d65f4f0b510610d7cd9d215cfb106132da4582582d0a05282+image_tiny+imagen_tiny.png

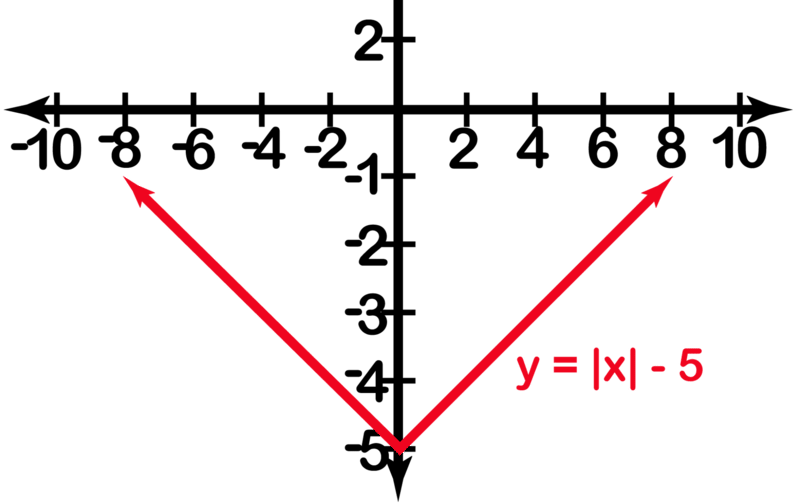
La gráfica de y=|x|−5 está abajo. Es claro que el -5 después del valor absoluto hace que la gráfica se desplace hacia abajo 5 lugares.

F-d_2068b72a1e8e844a8b89dded585198bd395b28205274c674fed50af9+image_tiny+imagen_tiny.png

“frameborder="0" height="450px” name="97623" src=” https://www.ck12.org/flx/show/video/...ions-Example-2 "style="font-size: 1.1rem;” thumbnailurl= "” title="VideoObject? hash=970caf6dfce48151c1f900b8c2c3ea11" uploaddate="2016-06-30 22:20:35 "width=” 95% “>

Revisar

Para las preguntas 1-5, identificar la familia a la que pertenece cada función.

y=|x−7|
y=3x−4
f (x) =|x ² |
|x|−2=y
\(\ f(x)=x+\frac{3 x}{2}\)
Grafica a mano la siguiente función por partes:\ (\ f (x) =\ left\ {\ begin {array} {l}
x, x\ geq 0\\
-x, x<0
\ end {array}\ right.\)
En tu calculadora gráfica, grafica la función f (x) =|x|−2 y responde las siguientes preguntas: a. ¿Cuál es la forma de la gráfica? b. Compare la gráfica con la gráfica en el problema anterior. ¿Cuál es la diferencia entre las dos gráficas? c. ¿Cuál es la pendiente de las dos líneas que crean la gráfica?

Para cada ecuación que sigue, identifica las coordenadas del vértice de la gráfica, sin realmente graficar.

f (x) =|6x|
f (x) =|x−6|+8
f (x) =|x+7|−8
f (x) =|x+5|
A continuación se muestra la gráfica de p (x) =|x|. Si t (x) =−|x|−3, ¿en qué se diferenciará la gráfica de t (x) de la gráfica de p (x)?
Grafica la ecuación del valor absoluto, crea tu propia tabla para justificar los valores: f (x) =|x−3|
Grafica la ecuación del valor absoluto, crea tu propia tabla para justificar valores: g (x) =|x+3|

Identificar la función padre para cada conjunto de funciones lineales. Grafica cada conjunto de funciones usando una calculadora gráfica. Identificar similitudes y diferencias de cada conjunto.

a. f (x) =x−7, b. f (x) =x−2, c. f (x) =x+1, d. f (x) =x+5, e. f (x) =x+10
Función Parent:

Similitudes:

Diferencias:

\(\ \text{a. } f(x)=\frac{2}{11} x, \text { b. } f(x)=\frac{1}{2} x, \text { c. } f(x)=\frac{2}{3} x\)
Función Parent:

Similitudes:

Diferencias:

a. f (x) =x−7, b. f (x) =2x, c. f (x) =4x, d. f (x) =2x+5, e. f (x) =6x−10
Función Parent:

Similitudes:

Diferencias:

Usa la forma estándar de una ecuación lineal: f (x) =ax+b y tus investigaciones anteriores para ayudarte a responder las siguientes preguntas.
¿Cómo afecta el valor a a la gráfica?
¿Cómo afecta el valor b a la gráfica?
¿Cómo son los valores de dominio similares/diferentes?
¿Cómo son los valores de rango similares/diferentes?
¿Afecta el valor a y/o b al dominio?
¿Afecta el valor a y/o b al rango?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.10.

El vocabulario

Término	Definición
Valor Absoluto	El valor absoluto de un número es la distancia que el número es de cero. Los valores absolutos nunca son negativos.
Función de valor absoluto	Una función de valor absoluto grafica una forma de V, y está en la forma y=\|x\|.
Familias de funciones	Las familias de funciones son grupos de funciones con similitudes que hacen que sean más fáciles de graficar cuando se está familiarizado con la función padre, el ejemplo más básico de la forma.
Familia de funciones	Las familias de funciones son grupos de funciones con similitudes que hacen que sean más fáciles de graficar cuando se está familiarizado con la función padre, el ejemplo más básico de la forma.
ecuación lineal	Una ecuación lineal es una ecuación entre dos variables que produce una línea recta cuando se grafica.
Función Lineal	Una función lineal es una relación entre dos variables que produce una línea recta cuando se grafica.
función padre	Una función padre es la forma más simple de un tipo particular de función. Todas las demás funciones de este tipo suelen compararse con la función padre.
Función definida por partes	Una función definida por partes es una función que junta dos o más partes de otras funciones para crear una nueva función.