1.7.1: Modelos lineales y cuadráticos

Última actualización
Guardar como PDF

Page ID: 109011

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Modelos lineales y cuadráticos

Aprender a expresar situaciones de la vida real como funciones matemáticas permite que las ideas y acciones aparentemente complejas se descompongan en partes más pequeñas y simples y se analicen.

¿Cómo podría expresar matemáticamente lo siguiente?

Dos hermanos deciden correr a casa desde la escuela, tomando diferentes rutas. El segundo hermano sale 5 minutos después del primero, y ambos llegan a casa al mismo tiempo.

Modelos lineales y cuadráticos

Modelos Lineales

Las funciones más simples son generalmente modelos lineales. Por ejemplo, la ecuación y = 3 x podría usarse para representar cuánto dinero traerías si vendieras x cajas de galletas por $3 por caja. Muchas situaciones se pueden modelar con funciones lineales. La idea clave es que alguna cantidad en la situación tenga una tasa de cambio constante. En el ejemplo de venta de cookies, cada caja cuesta $3.00. Por lo tanto, las ganancias aumentan a una tasa constante. En suma, las funciones lineales se utilizan para modelar una situación de cambio constante, ya sea de aumento o disminución.

Modelos cuadráticos

Las funciones cuadráticas también pueden ser utilizadas como modelos. Por ejemplo, la función$\ A(x)=50 x-\frac{x^{2}}{2}$ podría ser utilizada para representar el área de un terreno rectangular encerrado en tres lados por 100 pies de barda. Este modelo podría ser utilizado para identificar el área máxima posible para la parcela de tierra.

Otro ejemplo es una situación en la que se lanza una pelota al aire. El balón viajará hacia arriba, y luego viajará hacia abajo hasta que golpee el suelo. ¿Qué tan alto irá la pelota? ¿Cuándo llegará al suelo? Este tipo de situación puede ser modelada por una función de la forma h (t) = -16 t ² + v ₀ t + h ₀. La variable t representa el tiempo desde que se lanzó el balón. El coeficiente v ₀ representa la velocidad inicial de la pelota, y la constante h ₀ representa la altura inicial de la pelota. La constante -16 proviene de la fuerza de gravedad que tira de la pelota hacia abajo, razón por la cual es negativa. El ejemplo 3 muestra una situación específica de esta forma.

Ejemplos

Ejemplo 1

Solución

Anteriormente, se le pidió que elaborara un modelo matemático para la siguiente afirmación.

Dos hermanos deciden correr a casa desde la escuela, tomando diferentes rutas. El segundo hermano sale 5 minutos después del primero, y ambos llegan a casa al mismo tiempo.

Hay varias formas diferentes de modelar la información, dependiendo de qué parte (s) de la información elija utilizar. Un par de ejemplos incluyen:

Si t = el tiempo que tardó el segundo hermano en llegar a casa, entonces t + 5 = el tiempo que tardó el primer hermano.

Si t = el tiempo que tardó el primer hermano en llegar a casa, entonces (t + (t - 5)) /2 representa el tiempo promedio para correr a casa.

Su modelo puede ser similar, o puede estar escrito de manera diferente, pero debe comparar diferentes valores dados en el problema de la historia.

Ejemplo 2

Dirige un negocio de corte de césped y cobra $15 por césped. Escribir una función lineal para describir la cantidad de dinero hecho en función del número de céspedes segados.

Solución

Si expresa el número de céspedes segados como l, entonces $15 multiplicados por l representarían el dinero total realizado con base en el número de céspedes, por lo tanto:

ingreso total = 15* l

Ejemplo 3

Se deja caer una roca del borde de un acantilado, y cronometra la caída en segundos. Determinar la función que modela la altura del acantilado en función del tiempo de caída en segundos.

Solución

Con una velocidad inicial de 0, la altura del acantilado se puede calcular con la fórmula: h (t) = 16t ².

Ejemplo 4

Estás parado en el techo de un edificio que está a 20 pies sobre el suelo. Lanzas una bola al aire con una velocidad vertical inicial de 40 pies/seg, para que aterrice en el suelo, no en el techo. ¿Qué tan alto irá la pelota y cuándo alcanzará su máxima altura? ¿Cuándo golpeará la pelota al suelo?

Solución

Primero necesitamos escribir una función para modelar la situación. Usando la forma general de la ecuación dada anteriormente, podemos escribir la función h (t) = -16t ² + 40t + 20, donde h (t) representa la altura sobre el suelo.

Para responder a la primera pregunta, necesitamos examinar la gráfica de la función. Si graficas esta ecuación en tu calculadora, necesitarás determinar una buena ventana de visualización. Una forma de comenzar a determinar una buena ventana es tomar en cuenta la intercepción y de la función. En este caso, la intercepción y es (0, 20). Piensa en qué tipo de función es esta: una parábola, orientada hacia abajo. Este hecho debería llevarte a pensar que necesitamos mirar los valores y muy por encima de 20. A menudo es útil mirar una tabla de valores. Usando la capacidad de “preguntar” de la calculadora, si ingresa valores x de 1, 2 y 3, verá que la función sube a 44 en x = 1. El valor máximo es muy probable en algún lugar cercano a x = 1. Presione VENTANA y establezca xmin = 0, xmax = 3. Después establece Ymin = 0 (o un poco menos, si quieres ver el eje y). Ymax debe ser no menos de 44, aunque es posible que desee hacerlo más grande, como 50 o más, solo para estar seguro de que puede ver el vértice. Una vez que haya configurado la ventana, presione GRAPAR.

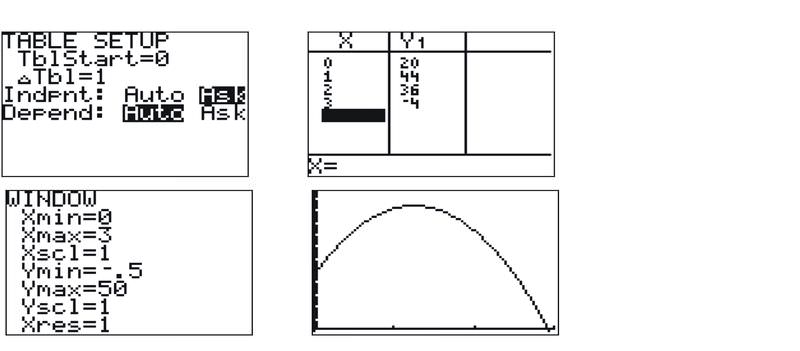
F-d_a1c51cdf096df6a582edbf2c985428c3d022ab4a70d9c280ba0a8725+image_tiny+image_tiny.jpg

Ahora deberías ver la parábola. Para identificar las coordenadas del vértice, puede usar la función MAX en el menú CALC. Recuerda que la calculadora te pedirá que ingreses un límite izquierdo, un derecho y una conjetura para el máximo. Si usa la función MAX, debe encontrar que las coordenadas del vértice son (1.25, 45). Esto significa que 1.25 segundos después de que la pelota es lanzada al aire, alcanza una altura máxima de 45 pies.

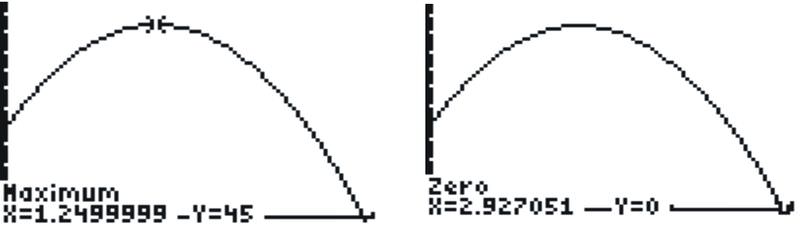
f-d_f45d97ba116ec8d41608d8f0ec092df681f82eb48491e858351063e3+image_tiny+image_tiny.jpg

Ahora, para responder a la segunda parte de la pregunta, necesitamos determinar cuándo la altura de la pelota es 0. Gráficamente, estamos buscando la intercepción x de la parábola. Si regresas a la pantalla GRÁFICO, deberías ver que la intercepción x es alrededor de 3. Si queremos determinar el valor exacto, o al menos una buena aproximación de la intercepción x, podemos usar la función ZERO. Presiona 2 ^nd TRACE para obtener el menú CALC, y elige la opción 2, CERO. Al igual que la función MAX, necesita ingresar un límite izquierdo, un límite derecho y una conjetura, aunque la suposición es opcional, solo presione ENTRAR. (Tenga en cuenta que la calculadora funciona de esta manera porque le está pidiendo que identifique qué x -intercepción calcular. La parábola tiene dos intercepciones x, y otras funciones pueden tener más.) Usando la función ZERO, debe encontrar que la intercepción x es aproximadamente 2.93. Esto significa que la pelota llega al suelo en poco menos de 3 segundos.

Ejemplo 5

La clase de primer año de Arlington quiere tener una recaudación de fondos. La clase quiere comprar una cantidad de $4.00 chanclas y $5.00 gorras de béisbol, y tiene un total de $100 para gastar.

Solución

Para expresar esta información en función, recuerde que la pregunta especificaba que había 100 dólares para gastar, y que cualquier dinero que no se gastara en sombreros (a $5 ea) se gastaba en chanclas (a $4 ea).

Si f representa el número de chanclas y b representa el número de gorras de béisbol, escriba una función para representar el número de chanclas compradas en función del dinero no gastado de las gorras de béisbol.
$\ \therefore f=\frac{\$ 100-5 h}{4}$
Usando su ecuación de (a), determine el número de gorras de béisbol que se pueden comprar si se compraron 10 chanclas.
Para calcular cuántos sombreros podrían comprarse si se compraran 10 pares de chanclas, sustituya 10 in por f, y resuelva por h:

\ (\\ begin {array} {l}
10=\ frac {100-5 h} {4}\\
40=100-5 h\\
5 h=60\\
h=12
\ end {array}\)

Por lo tanto, si se compraran 10 pares de chanclas, quedaría dinero para comprar 12 gorras de béisbol.

Ejemplo 6

Los estudios del metabolismo del alcohol muestran consistentemente que el contenido de alcohol en sangre (BAC) disminuye linealmente, después de aumentar rápidamente después de la ingestión inicial. En un estudio, el BAC en una persona en ayunas aumentó a aproximadamente 0.018% después de una sola bebida. Después de una hora el nivel había bajado a 0.010%.

Solución

Para responder a la pregunta, debes expresar la relación como una ecuación y luego usar la ecuación.

Primero, defina las variables en la función y cree una tabla.

Las dos variables son tiempo y BAC.

Tiempo	BAC
0	0.018%
1	0.010%

A continuación, calcule la tasa de cambio.

Tiempo	BAC	Tasa de cambio
0	0.018%	0
1	0.010%	(0.008%)

Esta tasa de cambio significa que cuando el tiempo aumenta en 1, el BAC disminuye (ya que la tasa de cambio es negativa) en .008. Es decir, el BAC está disminuyendo .008% cada hora. Ya que se nos dice que el BAC disminuye linealmente, podemos suponer que esa cifra se mantiene constante.

Escribir una ecuación que relacione BAC con el tiempo en horas después de beber t.
Ahora podemos escribir una ecuación con b representando BAC y t, el tiempo en horas:

b=−.008t+.018
Suponiendo que BAC continúe disminuyendo linealmente (es decir, a una tasa de cambio constante), aproximadamente ¿cuándo bajará el BAC a 0.002%?
Para saber cuándo alcanzará el BAC .002%, sustituirá .002 por b y resolverá por t.

.002=−.008t+.018

−.016=−.008t

t=2

Por lo tanto, el BAC alcanzará el .002% después de 2 horas.

Revisar

De 2002 a 2009 el número de estaciones de servicio en un determinado país aumentó en 100 estaciones por año. En 2004 había 1100 estaciones de servicio. Escribir una ecuación lineal para el número de estaciones de servicio, (y), en función del tiempo, (t,) donde t = 0 representa el año 2002.

Encuentra el vértice de las siguientes funciones cuadráticas y luego graficarlas.

f (x) =2x ² −6x+11
f (x) =3 (x+5) ² −2

En la celebración de fuegos artificiales del 4 de julio en el centro local, los fuegos artificiales son disparados por control remoto al aire desde un pozo en el suelo que está a 12 pies debajo de la superficie terrestre.

Encuentra una ecuación que modele la altura de una bomba aérea t segundos después de ser disparada hacia arriba con una velocidad inicial de 80 pies/seg. Supongamos que la bomba desacelera a una velocidad de 30 pies/seg cada segundo
Encuentra el vértice de la función cuadrática.
¿Cuál es la altura máxima sobre el nivel del suelo que alcanzará la bomba aérea?
¿Cuántos segundos después de su lanzamiento tardará en alcanzar esa altura?
Se lanza una roca desde lo alto de un edificio de 763 pies de altura. La distancia, en pies, entre la roca y el suelo t segundos después de su lanzamiento viene dada por d=−16t ² −2t+763. ¿Cuánto tiempo después de que se lanza la roca está a 430 pies del suelo?
Usa la fórmula de movimiento vertical h=−16t ² +v ₀ t+s para encontrar el número de segundos que tarda un cohete lanzado desde tierra con una velocidad inicial de 96 pies/s para alcanzar una altitud de 45 pies. Respuestas redondas a la décima más cercana.
La función P=0.0089T ² +1.1149t+78.4491 modela la población de Estados Unidos en millones desde 1900. Utilizar la función P para predecir el año en que la población supera los mil millones.
¿Para qué valor de x es f (x) =−10 si f (x) =−4x ² +3x?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.17.

El vocabulario

Término	Definición
modelo lineal	Un modelo lineal es una función lineal que representa una situación que implica una tasa de cambio constante.
Modelo	Un modelo es una expresión o función matemática utilizada para describir un elemento o situación física.
modelo cuadrático	Un modelo cuadrático es una función que representa una situación con una tasa de cambio que es un valor cuadrado. La gráfica de una función cuadrática es una parábola.