2.2.3: Calculadora gráfica para analizar funciones polinomiales
- Page ID
- 108611
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Graficando Funciones Polinómicas con una Calculadora Gráfica
Para hacer una carrera justa entre un dragster y un auto divertido, un científico ideó la siguiente ecuación polinómica:
f (x) =71.682x−60.427x 2 +84.710x 3 −27.769x 4 +4.296x 5 −0.262x 6. ¿Cuál es el punto máximo de la gráfica de esta función?
Fuente: Universidad del Arroz
Graficar funciones polinómicas con una calculadora
Ya has usado la calculadora gráfica para graficar parábolas. Ahora, ampliaremos ese conocimiento y graficaremos polinomios de mayor grado. Entonces, usaremos la calculadora gráfica para encontrar los ceros, máximos y mínimos.
Vamos a graficar f (x) =x 3 +x 2 −8x−8 usando una calculadora gráfica.
Estas instrucciones son para un TI-83 o 84. Primero, presione Y=. Si hay alguna función en esta ventana, elimínelas resaltando el signo = y presionando ENTRAR. Ahora, en Y1, entra en el polinomio. Debería verse así: x 3+x 2−8x−8. Presione GRAPH.
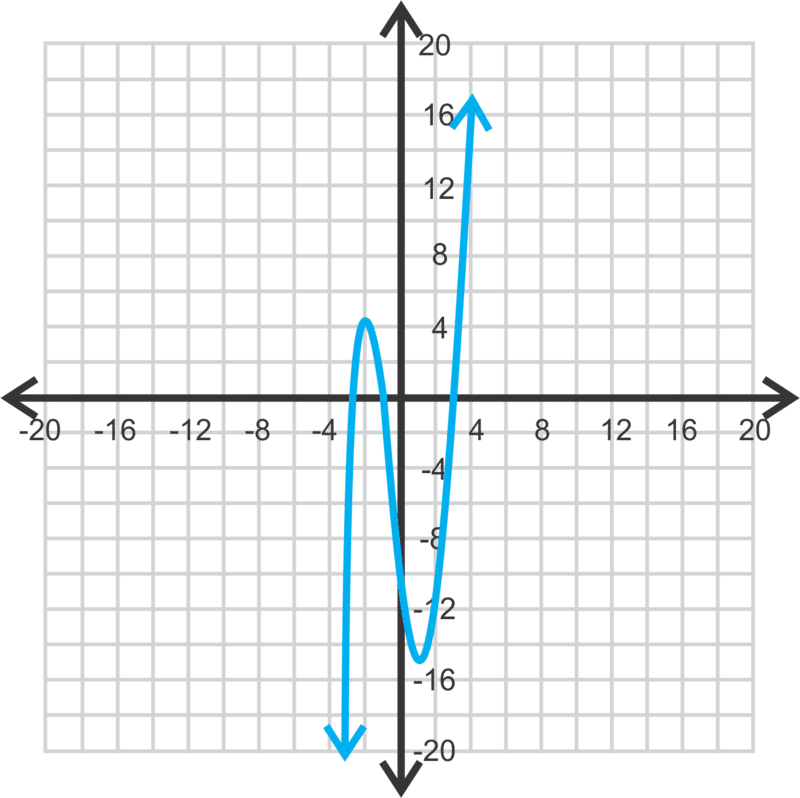
Para ajustar la ventana, presione ZOOM. Para obtener la típica pantalla -10 a 10 (para ambos ejes), presione 6:ZStandard. Para alejar el zoom, presione ZOOM, 3:ZoomOut, ENTER, ENTRAR. Para esta función en particular, la ventana necesita ir de -15 a 15 tanto para x como para y. Para ingresar manualmente la ventana, presione VENTANA y cambie el Xmin, Xmax, Ymin e Ymax para que pueda ver los ceros, mínimo y máximo. Tu gráfica debería parecerse a la de arriba.
Ahora, encontremos los ceros, máximo y mínimo de la función del problema anterior anterior.
Para encontrar los ceros, presione 2 nd TRACE para obtener el menú CALC. Seleccione 2: Cero y se le preguntará “¿Izquierda?” por la calculadora. Mueve el cursor (pulsando el ↑ o ↓) para que quede justo a la izquierda de un cero. Presione ENTER. Entonces, preguntará “¿Encuadernado a la derecha?” Mueve el cursor justo a la derecha de ese cero. Presione ENTER. Entonces la calculadora preguntará “¿Adivina?” En este punto, puedes ingresar en lo que creas que es el cero y volver a presionar ENTRAR. Entonces la calculadora te dará el cero exacto. Para la gráfica del problema anterior, necesitarás repetir esto tres veces. Los ceros son -2.83, -1 y 2.83.
Para encontrar el mínimo y el máximo, el proceso es casi idéntico a encontrar ceros. En lugar de seleccionar 2:Cero, seleccione 3:min o 4:max. El mínimo es (1.33, -14.52) y el máximo es (-2, 4).
Finalmente, encontremos la intercepción y−de la gráfica a partir del mismo problema anterior.
Si decides no usar la calculadora, conecta cero para x y resuelve para y.
f (0) =0 3 +0 2 −80−8
Usando la calculadora gráfica, presione 2 nd TRACE para obtener el menú CALC. Seleccione 1:valor. X= aparece en la parte inferior de la pantalla. Si hay un valor ahí, presione CLEAR para eliminarlo. Luego presione 0 y ENTRAR. La calculadora debería entonces decir “Y=−8”.
Ejemplos
Anteriormente, se le pidió que encontrara el punto máximo de la gráfica de la función.
Solución
Si enchufas la ecuación f (x) =71.682x−60.427x 2 +84.710x 3 −27.769x 4 +4.296x 5 −0.262x 6 en tu calculadora, encuentras que el máximo ocurre cuando x=6.15105. A ese valor de x, f (x) es igual a 1754.43. Por lo tanto, el punto máximo de la gráfica de la función es (6.15105, 1754.43).
Grafica y encuentra los valores críticos de las siguientes funciones.
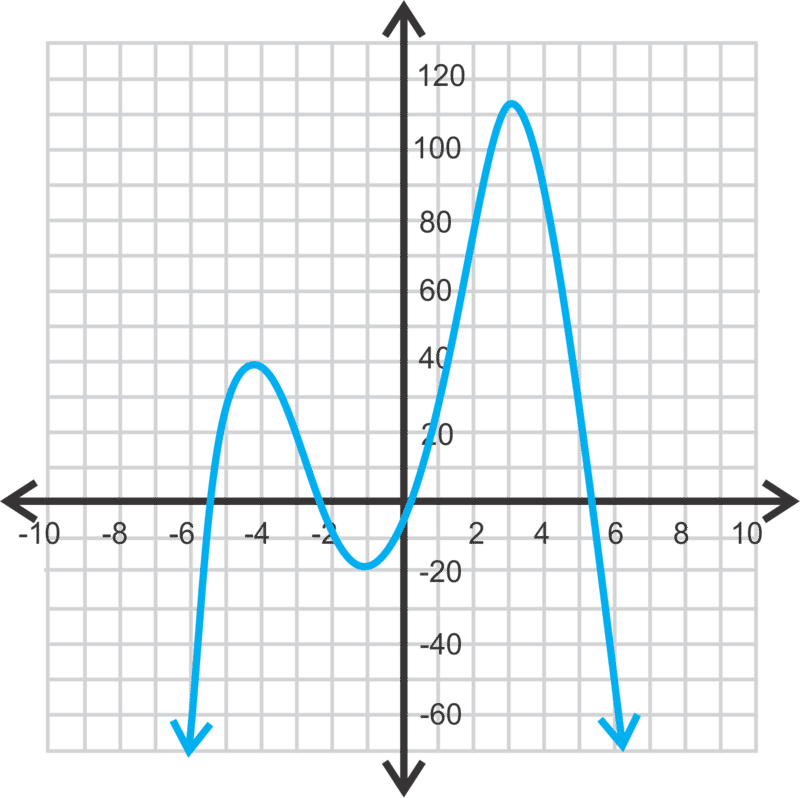
f (x) =-\(\ 1\over 3 \) x 4 −x 3 +10x 2 +25x−4
Solución
ceros: -5.874, -2.56, 0.151, 5.283
y−intercept: (0, -4)
mínimo: (-1.15, -18.59)
máximo local: (-4.62, 40.69)
máximo absoluto: (3.52, 113.12)
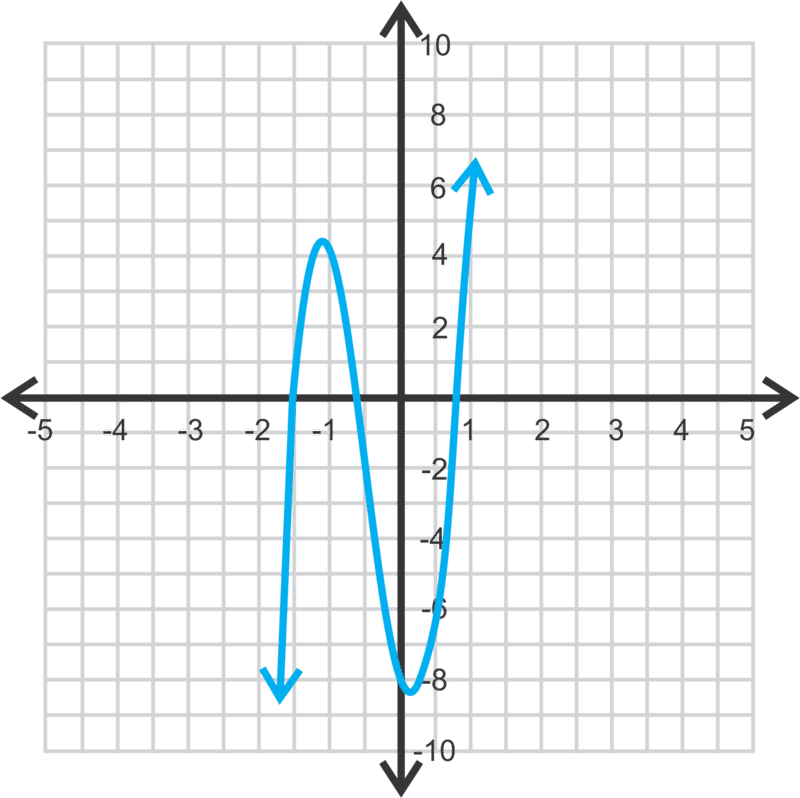
g (x) = 2x 5 −x 4 +6x 3 +18x 2 −3x−8
Solución
ceros: -1.413, -0.682, 0.672
y−intercept: (0, -8)
mínimo: (-1.11, 4.41)
máximo: (0.08, -8.12)
Encuentra el dominio y el rango de los Ejemplos 2 y 3.
Solución
El dominio del Ejemplo 2 es todos los números reales y el rango es todos los números reales menores que el máximo; (−∞ ,113.12]. El dominio y el rango del Ejemplo 3 son todos números reales.
Revisar
Gráfica las preguntas 1-6 en tu calculadora gráfica. Esboce la gráfica en una ventana apropiada. Luego, encuentre todos los valores críticos, dominio, rango y describa el comportamiento final.
- f (x) = 2x 3 +5x 2 −4x−12
- h (x) =−\(\ 1\over 4 \) x 4 −2x 3 −\(\ 13\over 4 \) x 2 −8x−9
- y=x 3 −8
- g (x) =−x 3 −11x 2 −14x+10
- f (x) =2x 4 +3x 3 −26x 2 −3x+54
- y=x 4 +2x 3 −5x 2 −12x−6
- ¿Cuáles son los tipos de soluciones en #2?
- Encuentra las dos soluciones imaginarias en #3.
- Encuentra los valores exactos de las raíces irracionales en #5.
Determinar si las siguientes afirmaciones son A VECES, SIEMPRE o NUNCA verdaderas Explica tu razonamiento.
- El rango de una función par es (−∞, max], donde max es el máximo de la función.
- El dominio y el rango de todas las funciones impares son todos números reales.
- Una función puede tener exactamente tres soluciones imaginarias.
- Un polinomio de n º grado tiene n soluciones reales.
- La gráfica padre de cualquier función polinómica tiene un cero.
- Desafío El valor exacto para uno de los ceros en #2 es −4+\(\ \sqrt{7}\). ¿Cuál es el valor exacto de la otra raíz? Entonces, usa esta información para encontrar las raíces imaginarias.
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.14.
El vocabulario
| Término | Definición |
|---|---|
| Raíces | Las raíces de una función son los valores de x que hacen y igual a cero. |