2.3.1: Gráficas de Funciones Racionales Básicas

Última actualización
Guardar como PDF

Page ID: 108618

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Graficar funciones racionales en forma estándar

La forma estándar de una función racional viene dada por la ecuación\(\ f(x)=\frac{a}{x-h}+k\). ¿Cuáles son las asíntotas de esta ecuación?

Función Racional

Una función racional está en la forma\(\ \frac{p(x)}{q(x)}\) donde\(\ p(x)\) están los polinomios y\(\ q(x)\) ≠ 0. La gráfica padre para las funciones racionales es\(\ y= \frac{1}{x}\), y la forma se llama hipérbola.

\(\ x\)	\(\ y\)
−4	\(\ -\frac{1}{4}\)
−2	\(\ -\frac{1}{2}\)
−1	−1
\(\ -\frac{1}{2}\)	−2
\(\ \frac{1}{2}\)	2
1	1
2	\(\ \frac{1}{2}\)
4	\(\ \frac{1}{4}\)

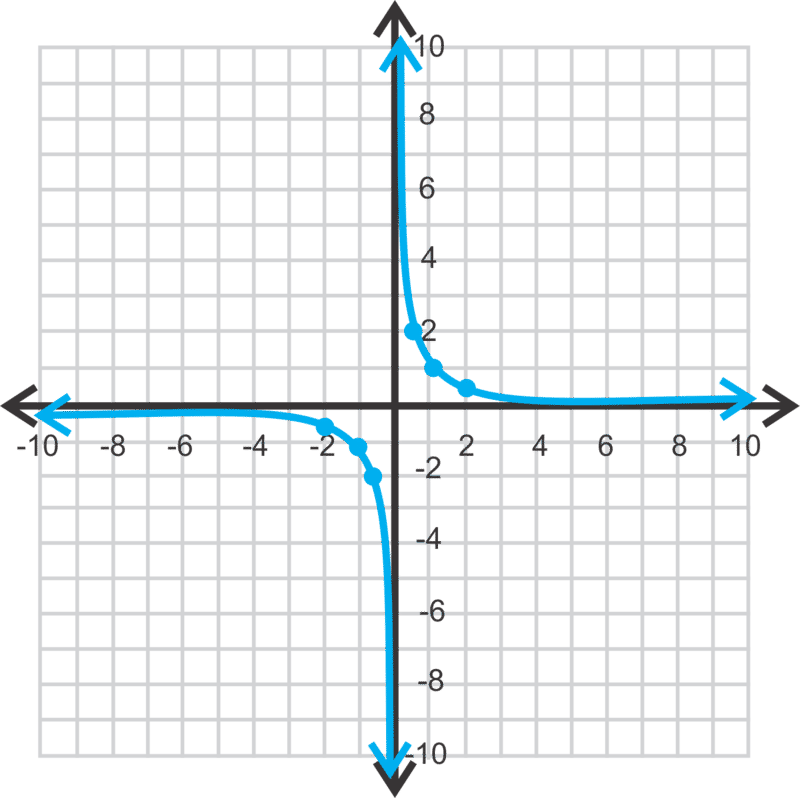F-D_5D237952794b84cfb484614d394468a7a4bbc1559f26880b828899be+image_tiny+image_tiny.png

Observe las siguientes propiedades de esta hipérbola: el eje x es una asíntota horizontal, el eje y es una asíntota vertical, y el dominio y el rango son todos números reales excepto donde están las asíntotas. Recordemos que la asíntota vertical es el valor que hace que el denominador sea cero porque no podemos dividir por cero. Para la asíntota horizontal, es el valor donde no se define el rango.

Las dos partes de la gráfica se llaman ramas. En el caso de una hipérbola, las ramas son siempre simétricas alrededor del punto donde se cruzan las asíntotas. En este ejemplo, son simétricos sobre el origen.

En esta lección, todas las funciones racionales tendrán la forma\(\ f(x)=\frac{a}{x-h}+k\)

Vamos a graficar\(\ f(x)=\frac{-2}{x}\) y encontrar cualquier asíntota, el dominio, rango, y cualquier ceros.

Hagamos una tabla de valores.

\(\ x\)	\(\ y\)
1	−2
2	−1
4	\(\ -\frac{1}{2}\)

Observe que estas ramas se encuentran en el segundo y cuarto cuadrantes. Esto se debe al signo negativo frente a la 2, o\(\ a\). Las asíntotas horizontales y verticales siguen siendo los\(\ y\) ejes\(\ x\) y. No hay ceros, ni\(\ x\) -intercepciones, porque el\(\ x\) eje -es una asíntota. El dominio y el rango son todos números reales distintos de cero (todos los números reales excepto cero).

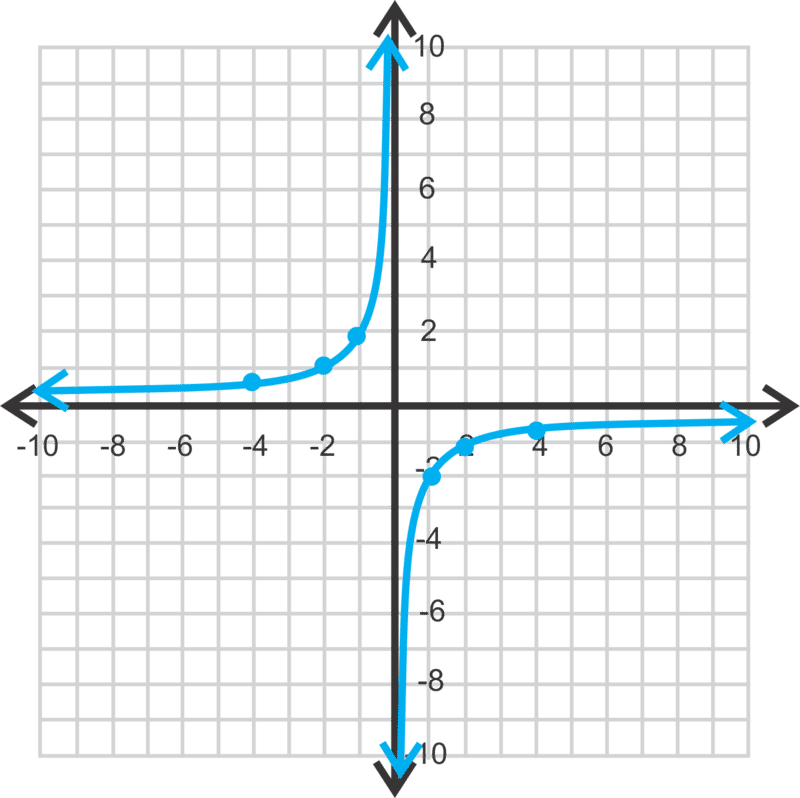f-d_a57d6138668ce80e6a5bc353b7c895a0244f3ab78d53aa8c8f806da1+image_tiny+image_tiny.png

Ahora, vamos a graficar\(\ y=\frac{1}{x-5}+2\) y encontrar todas las asíntotas, ceros, el dominio y el rango.

Para\(\ y=\frac{1}{x-5}+2\), la asíntota vertical es x=5 porque eso haría que el denominador sea cero y no podemos dividir por cero. Cuando x=5, el valor de la función sería\(\ y=\frac{1}{0}+2\), haciendo que el rango sea indefinido en\(\ y=2\). La forma y ubicación de las ramas son las mismas que la gráfica padre, simplemente desplazada hacia la derecha 5 unidades y hasta 2 unidades.

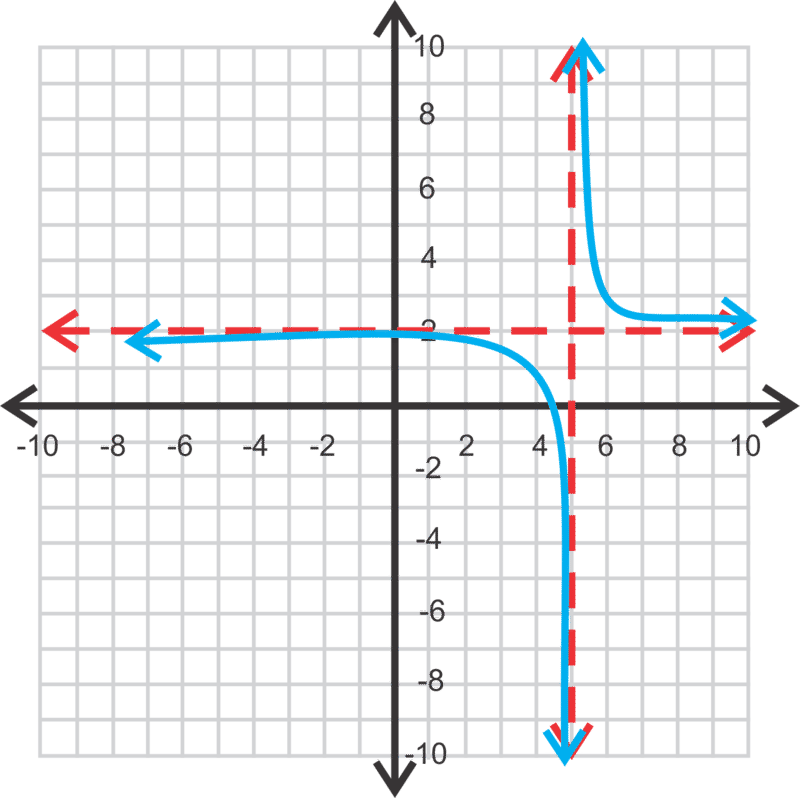f-d_81510ba66dee6434188ae574ed9ed699f8b1a2f05352940c7bf54d3b+image_tiny+image_tiny.png

Por lo tanto, para la forma general de una función racional,\(\ y=\frac{a}{x-h}+k, x=h\) es la asíntota vertical y\(\ y=k\) es la asíntota horizontal.

El dominio es todo números reales;\(\ x\) ≠ 5 y el rango es todo números reales;\(\ y\) ≠ 2. Para encontrar el cero, establezca la función igual a cero y resuelva para\(\ x\).

\ (\\ comenzar {alineado}
0 &=\ frac {1} {x-5} +2\\
-2 &=\ frac {1} {x-5}\
-2 x+10 &=1\\
-2 x &=-9\\
x &=\ frac {9} {2} =4.5
\ end {alineado}\)

Para encontrar la intercepción y, establezca x=0 y resuelva para y\(\ y=\frac{1}{0-5}+2=-\frac{1}{5}+2=1 \frac{4}{5}\).

Por último, encontremos la ecuación de la hipérbola a continuación.

Sabemos que el numerador será negativo porque las ramas de esta hipérbola están en el segundo y cuarto cuadrantes. Las asíntotas son x=−3 e y=−4. Hasta el momento, lo sabemos\(\ y=\frac{a}{x+3}-4\). Para determinar\(\ a\), podemos usar la intercepción x dada.

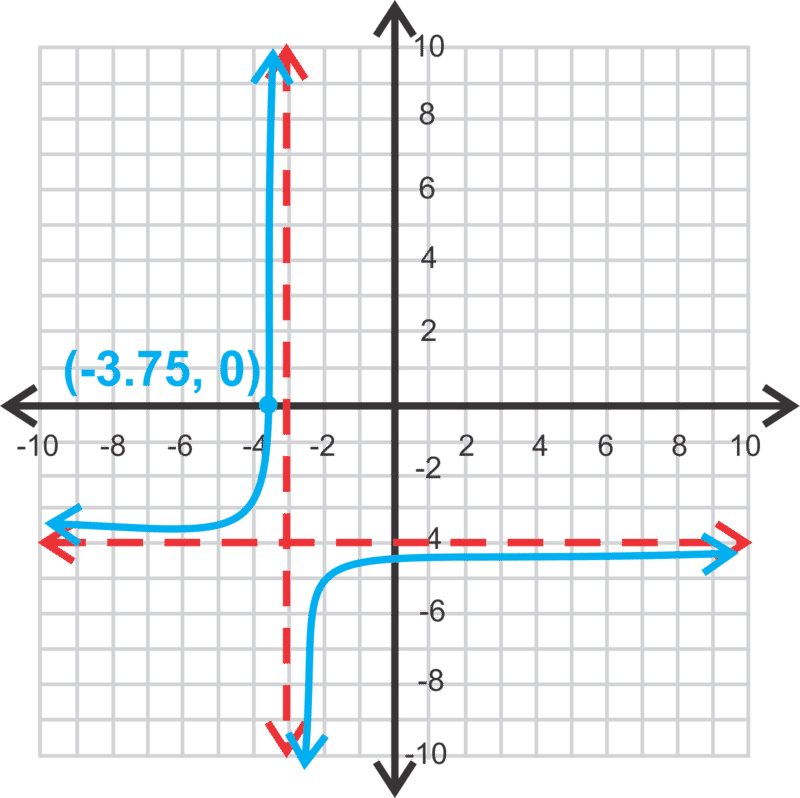f-d_99a873833acfd3cdf78ce6c10a81a065d1fdfd909a01ddcc4f0c5499+image_tiny+image_tiny.png

\ (\\ begin {alineado}
0&=\ frac {a} {-3.75+3} -4\\
4 &=\ frac {a} {-0.75}\ quad\ quad\ quad\ quad\ text {La ecuación es} y=\ frac {-3} {x+3} -4\\
-3 &=a
\ end {alineado}\)

Ejemplos

Ejemplo 1

Anteriormente, se le pidió que encontrara las asíntotas de la ecuación\(\ f(x)=\frac{a}{x-h}+k\).

Solución

De los problemas anteriores, hemos visto que la asíntota vertical ocurre cuando el denominador de la ecuación es igual a cero y la asíntota horizontal ocurre cuando el rango es indefinido.

Cuando\(\ x=h\), el denominador de\(\ f(x)=\frac{a}{x-h}+k\) es cero, también lo\(\ x=h\) es la asíntota vertical.

El valor de la función at\(\ x=h\) sería\(\ y=\frac{a}{0}+k\), haciendo que el rango fuera indefinido en\(\ y=k\).

Por lo tanto,\(\ y=k\) es la asíntota horizontal.

Ejemplo 2

¿Cuáles son las asíntotas para\(\ f(x)=\frac{-1}{x+6}+9\) Is (−5, −8) en la gráfica?

Solución

Las asíntotas son\(\ x=−6\) y\(\ y=9\). Para ver si el punto (−5, −8) está en la gráfica, sumételo por\(\ x\) y\(\ y\).

\ (\\ begin {aligned}
&-8=\ frac {-1} {-5+6} +9\ quad-8\ neq 8,\ text {por lo tanto, el punto} (-5, -8)\ text {no está en la gráfica.}\\
&-8=-1+9
\ end {alineado}\)

Para los Ejemplos 3 y 4, grafica las funciones racionales. Encuentra el cero, la intercepción y, las asíntotas, el dominio y el rango.

Ejemplo 3

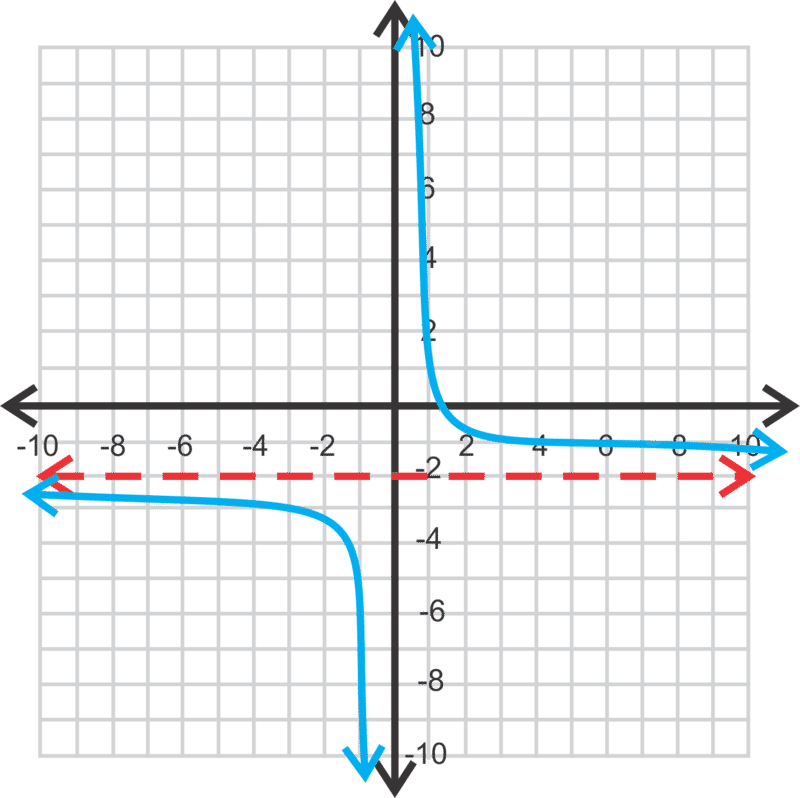
\(\ y=\frac{4}{x}-2\)

Solución

No hay intercepción y porque el eje y es una asíntota. La otra asíntota es y=−2. El dominio es todo números reales; x≠ 0. El rango es todos los números reales; y≠ −2. El cero es:

f-d_8a6a9b6eadfe05f1ac44c66feaea54222098baa1921615d91bd7d92e+image_tiny+image_tiny.png

\ (\\ comenzar {alineado}
0 &=\ frac {4} {x} -2\\
2 &=\ frac {4} {x}\\
2 x &=4\\
x &=2
\ end {alineado}\)

Ejemplo 4

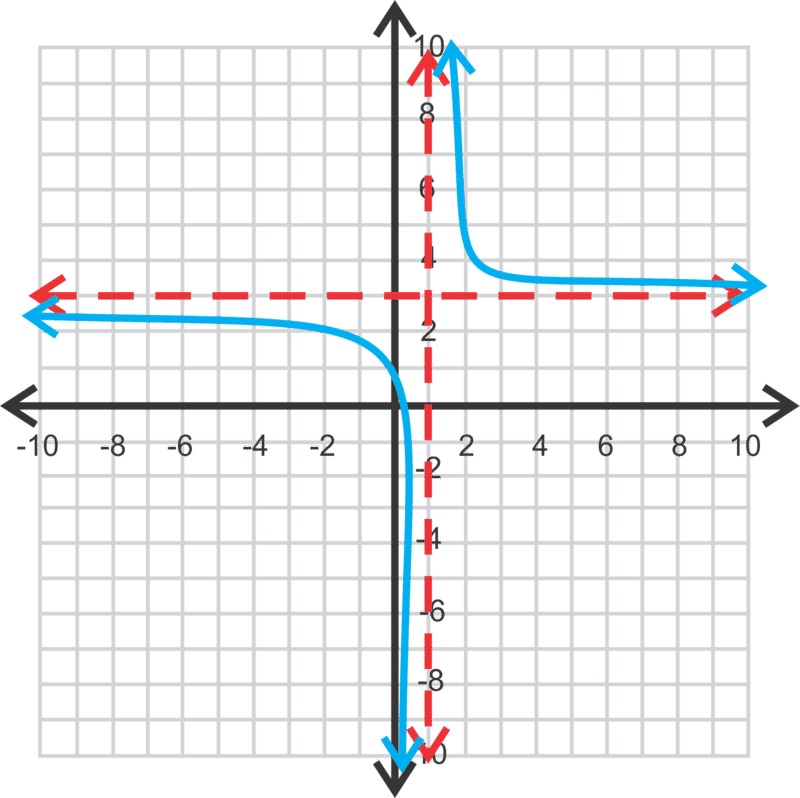
\(\ y=\frac{2}{x-1}+3\)

Solución

Las asíntotas son x=1 e y=3. Por lo tanto, el dominio es todo números reales excepto 1 y el rango es todo números reales excepto 3. La intercepción\(\ y=\frac{2}{0-1}+3=-2+3=1\) y es y el cero es:

f-d_46b96adb1579e2182a2fb6d193145570e257fa7b6f5a5f8a1e986083+image_tiny+image_tiny.png

\ (\\ comenzar {alineado}
0 &=\ frac {2} {x-1} +3\\
-3 &=\ frac {2} {x-1}\\
-3 x+3 &=2\\
-3 x &=-1\ fila derecha x=\ frac {1} {3}
\ final {alineado}\)

Ejemplo 5

Determinar la ecuación de la hipérbola.

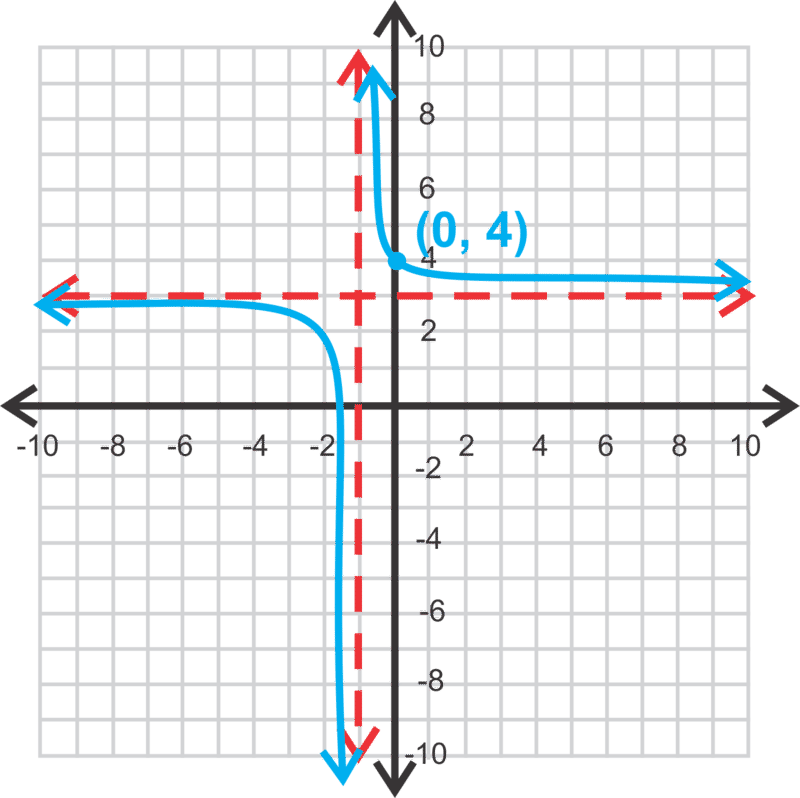
f-d_633212d1d908017ac4959f80b0bd5aa6d65e3d285392191ac848c41d+image_tiny+image_tiny.png

Solución

Las asíntotas son x=−1, y=3, haciendo la ecuación\(\ y=\frac{a}{x+1}+3\). Tomando la intercepción y, podemos resolver por un.

\ (\\ begin {alineado}
&4=\ frac {a} {0+1} +3\ quad\ text {La ecuación es} y=\ frac {1} {x+1} +3\\
&1=a
\ end {alineado}\)

Revisar

¿Para qué sirven las asíntotas\(\ y=\frac{2}{x+8}-3\)?
¿Es (−6, −2) un punto en la gráfica de #1?
¿Para qué sirven las asíntotas\(\ y=6-\frac{1}{x-4}\)?
¿Es (5,4) un punto en la gráfica de #3?

Para los problemas 5-13, graficar cada función racional, indicar las ecuaciones de las asíntotas, el dominio y rango y las intercepciones.

\(\ y=\frac{3}{x}\)
\(\ y=\frac{1}{x}+6\)
\(\ y=-\frac{1}{x}\)
\(\ y=-\frac{1}{x+3}\)
\(\ y=\frac{1}{x+5}\)
\(\ y=\frac{1}{x-3}-4\)
\(\ y=\frac{2}{x+4}-3\)
\(\ y=\frac{5}{x}+2\)
\(\ y=3-\frac{1}{x+2}\)

Escribe las ecuaciones de las hipérbolas. Se puede suponer que a = 1.

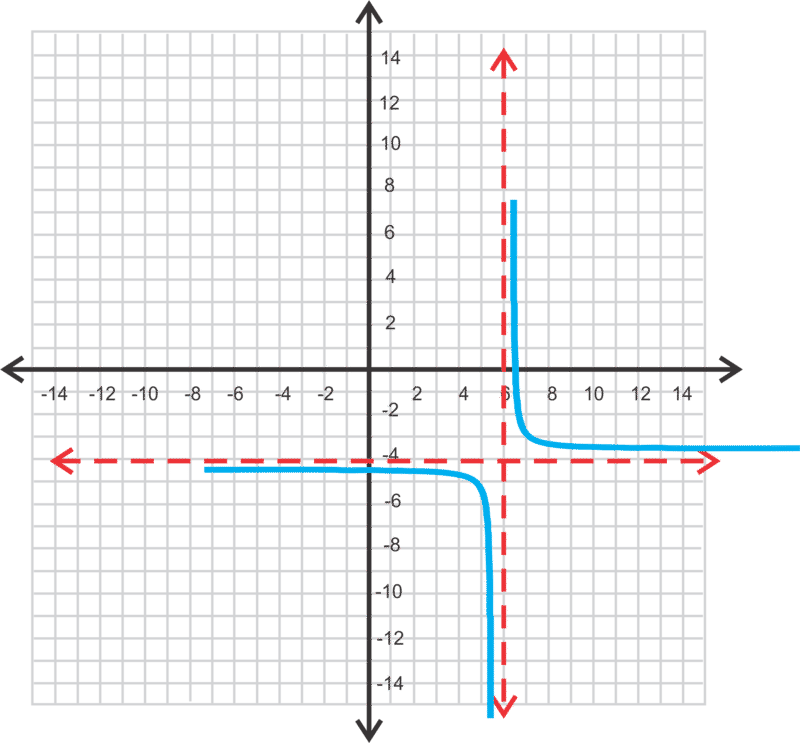[Figura5]
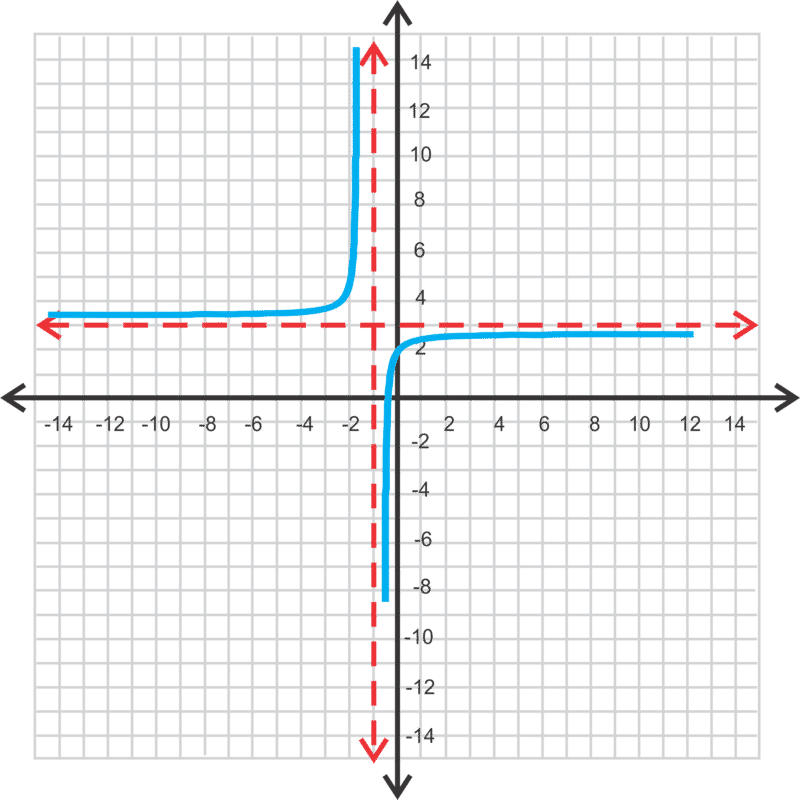[Figura6]

Respuestas para problemas de revisión

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.4.

vocabulario

Término	Definición
Sucursales	Las dos curvas de una hipérbola a veces se llaman ramas.
hipérbola	Una hipérbola es una sección cónica formada cuando el plano de corte cruza ambos lados del cono, dando como resultado dos curvas infinitas en forma de “U”.
Función Racional	Una función racional es cualquier función que pueda escribirse como la relación de dos funciones polinómicas.

Graficar funciones racionales en forma estándar

Función Racional

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Revisar

Respuestas para problemas de revisión

vocabulario

Atribuciones de imagen