2.3.3: Gráficas de Funciones Racionales cuando los Grados no son Iguales

Última actualización
Guardar como PDF

Page ID: 108601

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

Graficar cuando los Grados del Numerador y del Denominador son Diferentes

Xerxes dice que la función\(\ y=\frac{x-2}{4 x^{2}+7}\), tiene una asíntota horizontal de\(\ y=\frac{1}{4}\), Yolanda dice que la función no tiene asíntota horizontal, Zeb dice que sí tiene una asíntota horizontal pero está en y=0. ¿Cuál de ellos es correcto?

Graficar funciones racionales

En este concepto tocaremos las diferentes posibilidades para los tipos restantes de funciones racionales. Deberá usar su calculadora gráfica a lo largo de este concepto para asegurarse de que sus bocetos sean correctos.

Vamos a graficar\(\ y=\frac{x+3}{2 x^{2}+11 x-6}\) y encontrar todas las asíntotas, intercepciones, y el dominio y el rango.

En este problema el grado del numerador es menor que el grado del denominador. Siempre que esto suceda, la asíntota horizontal será y=0, o el eje x. Ahora, aunque el eje x es la asíntota horizontal, todavía habrá un cero en x=−3 (resolviendo el numerador para x y poniéndolo igual a cero). Las asíntotas verticales serán las soluciones a 2x ² +11x−6=0. Factorizando esta cuadrática, tenemos (2x−1) (x+6) =0 y las soluciones son\(\ x=\frac{1}{2}\) y −6. La intercepción y es\(\ \left(0,-\frac{1}{2}\right)\). En este punto, podemos conectar nuestra función a la calculadora gráfica para obtener la forma general.

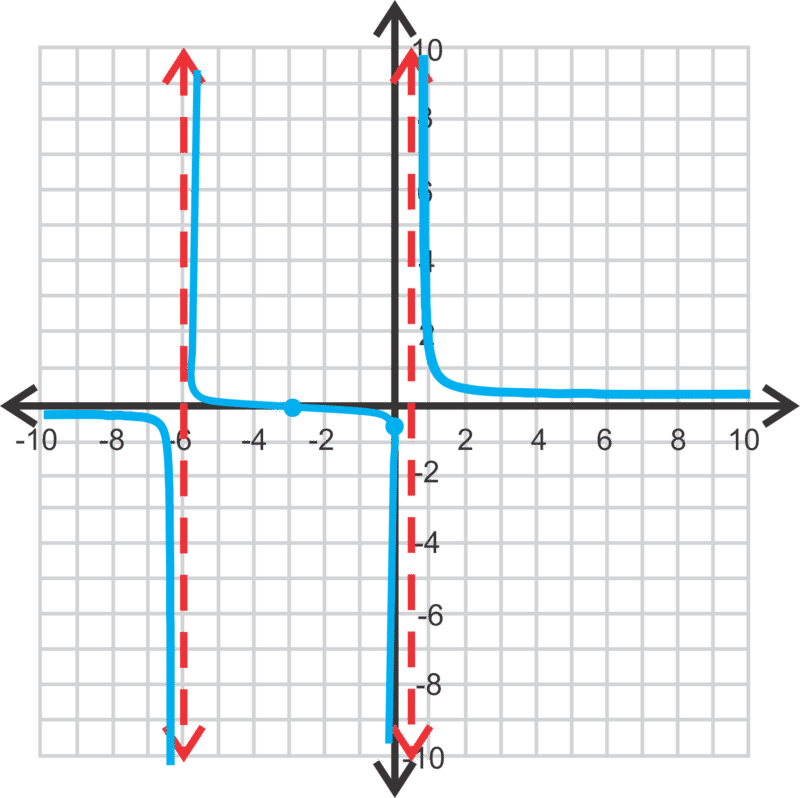
f-d_536edfef452f720366ac87fe8b6eb420cd50e2a8d2482713f3b26e62+image_tiny+image_tiny.png

Debido a que la porción media cruza sobre la asíntota horizontal, el rango será todo números reales. El dominio es\(\ x \in \mathbb{R} ; x=-6 ; x \neq \frac{1}{2}\).

Tenga cuidado a la hora de graficar cualquier función racional. Esta función no se parece a la gráfica de la izquierda en un TI-83/84. Esto se debe a que la calculadora no tiene la capacidad de dibujar las asíntotas por separado y quiere hacer que la función sea continua. Asegúrese de volver a verificar la tabla (2 ^nd → GRAPH) para encontrar dónde está indefinida la función.

Ahora, vamos a graficar\(\ f(x)=\frac{x^{2}+7 x-30}{x+5}\) y encontrar todas las asíntotas, intercepciones, y el dominio y el rango.

En este problema el grado del numerador es mayor que el grado del denominador. Cuando esto sucede, no hay asíntota horizontal. En cambio hay una asíntota inclinada. Recordemos que esta función representa división. Si tuviéramos que dividir x ² +7x−30 por x+5, la respuesta sería\(\ x+2-\frac{20}{x+5}\). La asíntota inclinada sería la respuesta, menos el resto. Por lo tanto, para este problema la asíntota inclinada es y=x+2. Todo lo demás es igual. La intercepción\(\ \frac{-30}{5} \rightarrow(0,-6)\) y es y las intercepciones x son las soluciones para el numerador, x ² +7x−30=0→ (x+10) (x−3) →x=−10,3. Hay una asíntota vertical en x=−5. En este punto, puedes probar algunos puntos para ver dónde están las sucursales o usar tu calculadora gráfica.

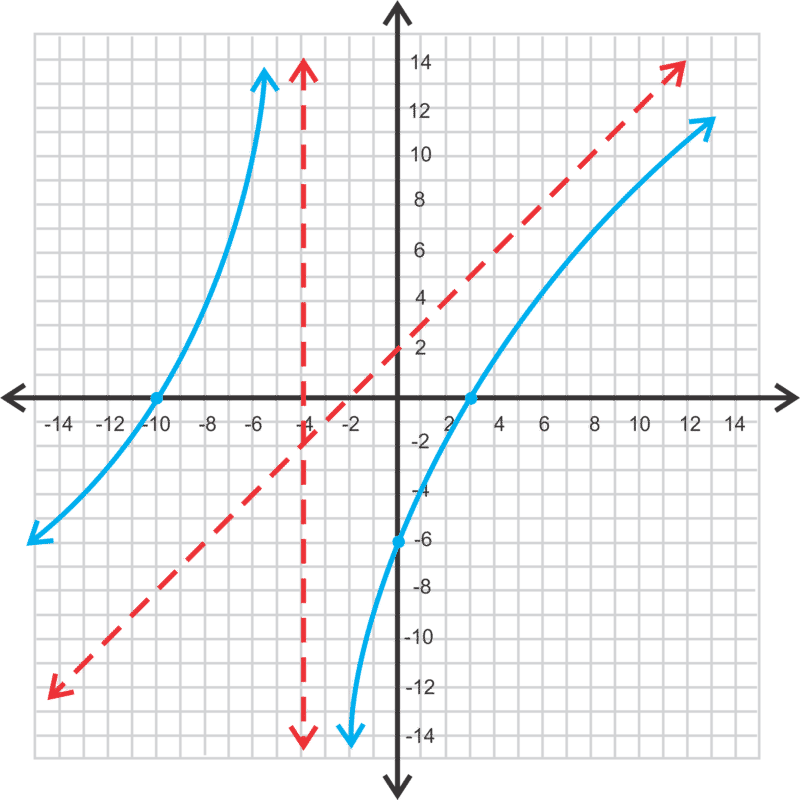F-D_7267868743fe75de7a292cbca95e2c654f54344c0f225e94fab86497+image_tiny+image_tiny.png

El dominio sería todos números reales; x≠ −5. Debido a la asíntota inclinada, no hay restricciones en el rango. Todo son números reales.

Por último, graficemos\(\ y=\frac{x-6}{3 x^{2}-16 x-12}\) y encontremos las asíntotas e intercepciones.

Debido a que el grado del numerador es menor que el grado del denominador, habrá una asíntota horizontal a lo largo del eje x. A continuación, encontremos las asíntotas verticales factorizando el denominador; (x−6) (3x+2). Observe que el denominador tiene un factor de (x−6), que es la totalidad del numerador. Eso significa que habrá un agujero en x=6.

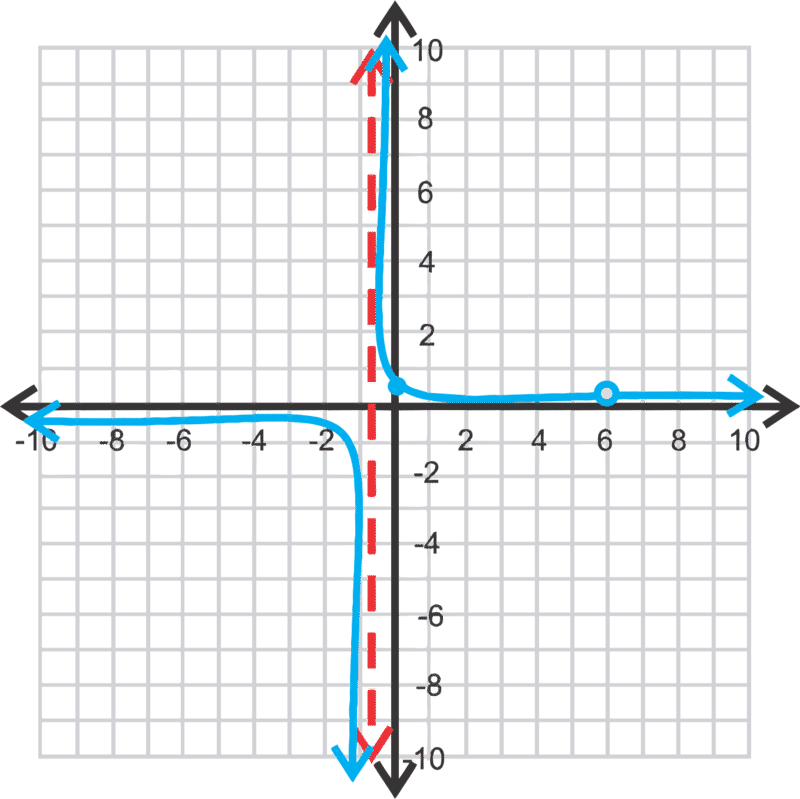
f-d_dc754448310e9a3ef3b0a6e1f9754d74e3a2cc212eb491c44365cf2c+image_tiny+image_tiny.png

Por lo tanto, la gráfica de\(\ y=\frac{x-6}{3 x^{2}-16 x-12}\) será la misma que\(\ y=\frac{1}{3 x+2}\) excepto con un agujero en x=6. No hay intercepción x, la asíntota vertical está en x=-\ frac {2} {3} y la intercepción y está\(\ \left(0, \frac{1}{2}\right)\).

Resumen

Para una función racional;\(\ f(x)=\frac{p(x)}{q(x)}=\frac{a_{m} x^{m}+\ldots+a_{0}}{b_{n} x^{n}+\ldots+b_{0}}\)

Si m<n, entonces hay una asíntota horizontal en y=0.
Si m=n, entonces hay una asíntota horizontal at\(\ y=\frac{a_{m}}{b_{n}}\) (relación de los coeficientes iniciales).
Si m>n, entonces hay una asíntota inclinada en\(\ y=\left(a_{m} x^{m}+\ldots+a_{0}\right) \div\left(b_{n} x^{n}+\ldots+b_{0}\right)\) sin el resto. En este concepto, sólo tendremos funciones donde m es una mayor que n.

Ejemplos

Ejemplo 1

Anteriormente, se le pidió que determinara qué estudiante es correcto.

Solución

El grado del numerador x−2 es menor que el grado del denominador 4x ² +7. Sabemos que siempre que esto suceda la asíntota horizontal será y=0, o el eje x.

Por lo tanto, Zeb tiene razón.

Grafica las siguientes funciones. Encuentra cualquier interceptación y asíntota.

Ejemplo 2

\(\ y=\frac{3 x+5}{2 x^{2}+9 x+20}\)

Solución

intercepción x:\(\ \left(-\frac{5}{3}, 0\right)\), intercepción y:\(\ \left(0, \frac{1}{4}\right)\)

asíntota horizontal: y=0

asíntotas verticales: ninguna

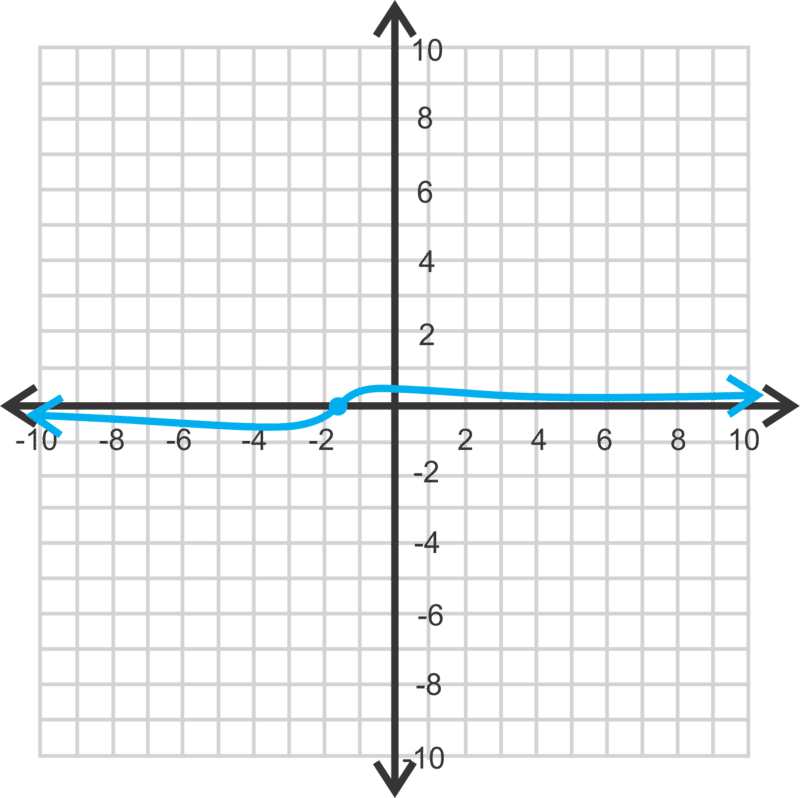f-d_c142cc9c51ce40ddb263e877033ec56061ca493a76508188c4c09010+image_tiny+image_tiny+image_tiny.png

Ejemplo 3

\(\ f(x)=\frac{x^{2}+4 x+4}{x^{2}-3 x-4}\)

Solución

intercepción x: (−2,0), intercepción y: (0, −1)

asíntota horizontal: y=1

asíntotas verticales: x=4 y x=−1

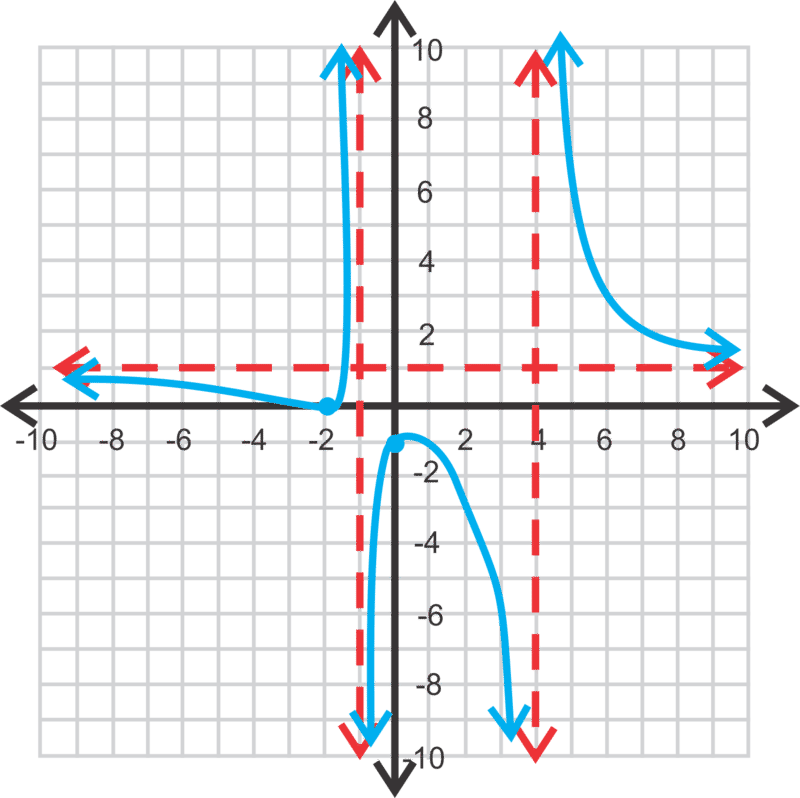f-d_b016693e7c2394e771f9a715d89ec9746041bd75802b13394d87acf1+image_tiny+image_tiny.png

Ejemplo 4

\(\ g(x)=\frac{x^{2}-16}{x+3}\)

Solución

intercepciones x: (−4,0) y (4,0)

Intercepción en Y:\(\ \left(0,-\frac{16}{3}\right)\)

asíntota inclinada: y=x−3

asíntotas verticales: x=−3

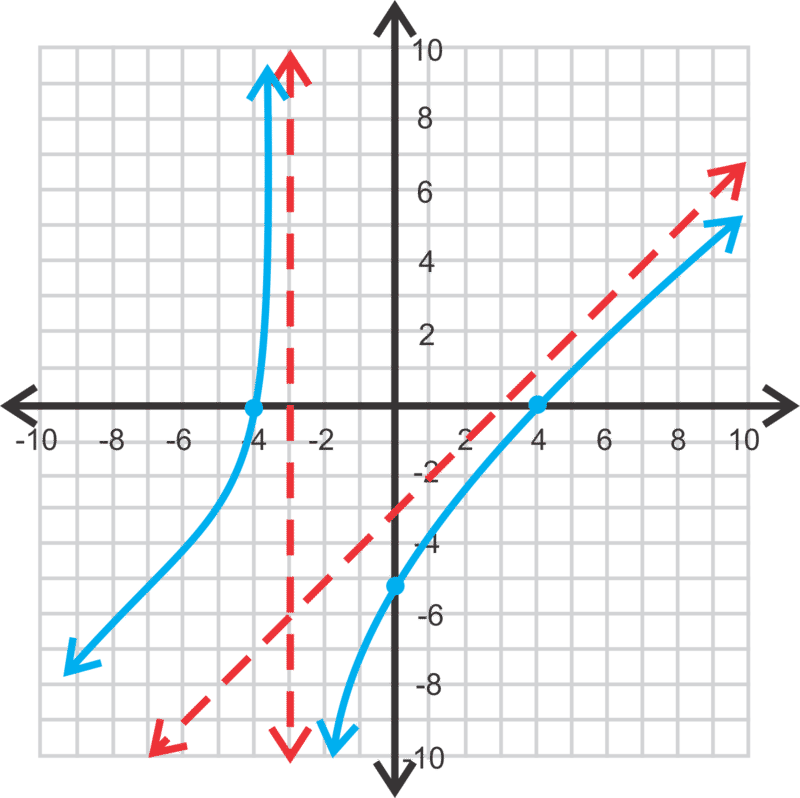
f-d_4390278c3cb44070b613e81066f31af26490d5a3a7f13a334c0298fe+image_tiny+image_tiny+image_tiny.png

Ejemplo 5

\(\ y=\frac{2 x+3}{6 x^{2}-x-15}\)

Solución

x-intercepts: ninguno, agujero en\(\ x=-\frac{3}{2}\)

Intercepción en Y:\(\ \left(0,-\frac{1}{5}\right)\)

asíntota horizontal: y=0

asíntota vertical:\(\ x=\frac{5}{3}\)

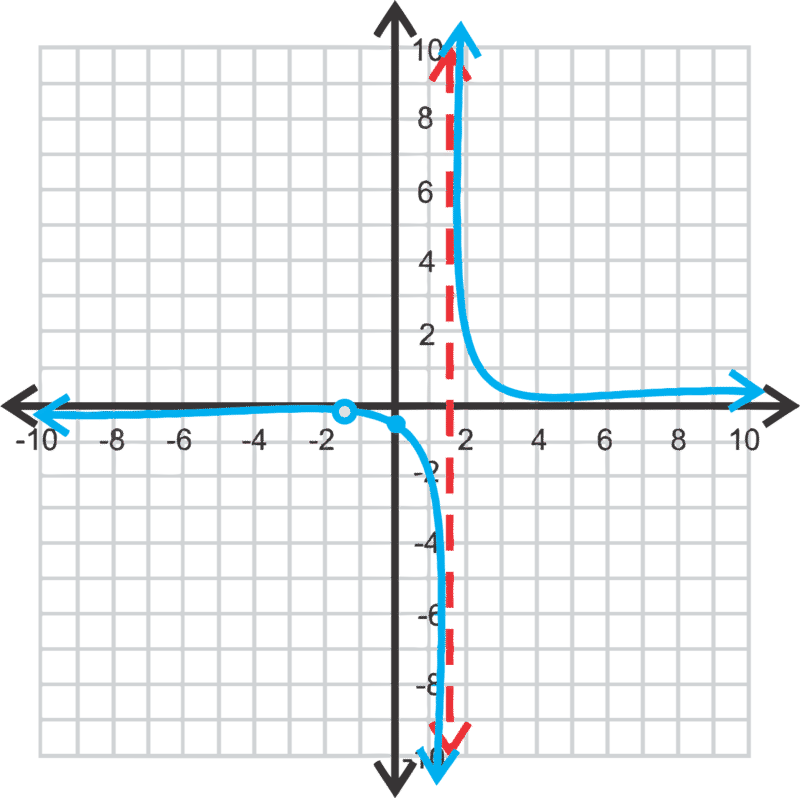
f-d_bcaf7e3d7cca8d903e9d9733c8aea81759a9e3d538337153ea5ba5f3+image_tiny+image_tiny.png

Revisar

Encuentra todas las asíntotas de las siguientes funciones.

\(\ y=\frac{x-2}{x^{2}+6 x+8}\)
\(\ y=\frac{x^{2}-4}{x+5}\)
\(\ y=\frac{x^{2}}{x-3}\)
Encuentra las x -intercepciones de la función en #2.
Encuentra las x -intercepciones de la función en #3.

Grafica las siguientes funciones. Encuentra cualquier interceptación, asíntota y agujeros.

\(\ y=\frac{x+1}{x^{2}-x-12}\)
\(\ f(x)=\frac{x^{2}+3 x-10}{x-3}\)
\(\ y=\frac{x-7}{2 x^{2}-11 x-21}\)
\(\ g(x)=\frac{2 x^{2}-2}{3 x+5}\)
\(\ y=\frac{x^{2}+x-30}{x+6}\)
\(\ f(x)=\frac{x^{2}+x-30}{2 x^{3}-5 x^{2}-4 x+3}\)
\(\ y=\frac{x^{3}-2 x^{2}-3 x}{x^{2}-5 x+6}\)
\(\ f(x)=\frac{2 x+5}{x^{2}+5 x-6}\)
\(\ g(x)=\frac{-x^{2}+3 x+4}{2 x-6}\)
Determinar la asíntota inclinada de\(\ y=\frac{3 x^{2}-x-10}{3 x+5}\). Ahora, grafica esta función. ¿Realmente hay una asíntota inclinada? ¿Puedes explicar tus resultados?

Respuestas para problemas de revisión

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.6.

El vocabulario

Término	Definición
Asymptota inclinada	Una asíntota inclinada es una línea diagonal que marca un rango específico de valores hacia los que la gráfica de una función puede acercarse, pero nunca alcanzará. Existe una asíntota inclinada cuando el numerador de la función es exactamente un grado mayor que el denominador. Una asíntota inclinada se puede encontrar a través de una división larga.

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Graficar cuando los Grados del Numerador y del Denominador son Diferentes

Graficar funciones racionales

Resumen

Ejemplos

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4

Ejemplo 5

Revisar

Respuestas para problemas de revisión

El vocabulario

Atribuciones de imagen