2.3.4: Prueba de Signos para Gráficas de Funciones Racionales
- Page ID
- 108599
Prueba de signos para gráficos de función racionales
Las asíntotas de una función racional proporcionan una estructura muy rígida en la que debe vivir la función. Una vez conocidas las asíntotas se debe utilizar el procedimiento de prueba de signos para ver si la función se vuelve cada vez más positiva o cada vez más negativa cerca de las asíntotas. Entonces, una pregunta de manejo se convierte en ¿qué tan cerca necesita estar cerca para que funcione la prueba de letreros?
Prueba de signos para funciones racionales
Considera sustituir mentalmente el número 2.99999 en la siguiente expresión racional.
\(\ f(x)=\frac{(x-1)(x+3)(x-5)(x+10)}{(x+2)(x-4)(x-3)}\)
Sin hacer nada de la aritmética, simplemente anote el signo de cada término:
\(\ f(x)=\frac{(+) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(-) \cdot(-)}\)
El único término en el que el valor es cercano a cero es (x−3) pero la resta cuidadosa aún indica un signo negativo. El producto de todos estos signos es negativo. Esta es una fuerte evidencia de que esta función se acerca al infinito negativo a medida que x se acerca a 3 desde la izquierda.
A continuación considere sustituir mentalmente 3.00001 y pasar por el mismo proceso.
\(\ f(x)=\frac{(+) \cdot(+) \cdot(-) \cdot(+)}{(+) \cdot(-) \cdot(+)}\)
El producto de todos estos signos es positivo, lo que significa que desde la derecha esta función se acerca al infinito positivo en su lugar. Esta técnica se llama prueba de signos. La prueba de signo es un procedimiento para determinar únicamente si una función está por encima o por debajo del eje en un valor particular.
La prueba de signos te ayuda a bosquejar y graficar una función. Mira la siguiente función:
\(\ f(x)=\frac{1}{(x+2)^{2} \cdot(x-1)}\)
Tu primer paso para bosquejar esto es identificar las asíntotas verticales. Las asíntotas verticales ocurren en x=−2 y x=1. Después, se utilizan las asíntotas para realizar una prueba de signos. Los puntos con los que se utilizará el procedimiento de prueba de señales son -2.001, -1.9999, 0.9999, 1.00001. El número de decimales sí importa siempre y cuando el número esté suficientemente cerca de la asíntota. Tenga en cuenta que cualquier número real al cuadrado es positivo.
\ (\\ begin {alineado}
f (-2.001) &=\ frac {(+)} {(+)\ cdot (-)} =-\\
f (-1.9999) &=\ frac {(+)} {(+)\ cdot (-)} =-\
f (0.9999) &=\ frac {(+)} {(+)\ cdot (-)} =-\\
f (1.0001) &=\ frac {(+)} {(+)\ cdot (+)} =+
\ end {alineado}\)
Posteriormente, cuando dibujes todo, usarás tus conocimientos de ceros e intercepciones. Por ahora, enfócate solo en las porciones de la gráfica cerca de las asíntotas. Tenga en cuenta que la siguiente gráfica NO está completa.
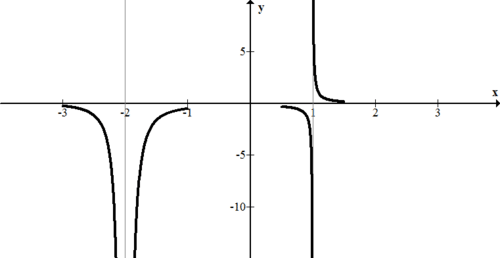 [Figura1]
[Figura1]Ejemplos
Anteriormente, se le preguntó qué tan cerca deben estar los números para realizar la prueba de signos.
Solución
Para responder verdaderamente a la pregunta sobre qué tan cerca deben estar los números, se debe usar el cálculo. A los efectos del Precálculo, el número de prueba debe estar más cerca de la asíntota vertical que cualquier otro número en el problema. Si la asíntota vertical ocurre en 3 y 3.01 está en el problema en otra parte, no elija 3.1 como número de prueba de signo.
Identificar las asíntotas verticales y utilizar el procedimiento de prueba de señales para esbozar aproximadamente la naturaleza de la función cerca de las asíntotas verticales.
\(\ f(x)=\frac{(x+1)(x-4)^{2}(x-1)(x+3)^{3}}{100(x-1)^{2}(x+2)}\)
Solución
Tenga en cuenta que x=−2 es claramente una asíntota. Inicialmente puede no estar claro si x=1 es una asíntota o un agujero. Al igual que los agujeros tienen prioridad sobre los ceros, las asíntotas tienen prioridad sobre los agujeros. Los cuatro valores para utilizar el procedimiento de prueba de signos son -2.001, -1.9999, 0.9999, 1.00001.
\ (\\ begin {alineado}
f (-2.001) &=\ frac {(-)\ cdot (+)\ cdot (-)\ cdot (+)} {(+)\ cdot (-)} =-\\
f (-1.9999) &=\ frac {(-)\ cdot (+)\ cdot (-)\ cdot (+)} {(+)\ cdot (+)} =+\\
f (0.9999) &=\ frac {(+)\ cdot (+)\ cdot (-)\ cdot (+)} {(+)\ cdot (+)} =-\\
f (1.0001) &=\ frac {(+)\ cdot (+)\ cdot (+)\ cdot (+)} {(+)\ cdot (+)} =+
\ end {alineado}\)
Un boceto del comportamiento de esta función cerca de las asíntotas es:
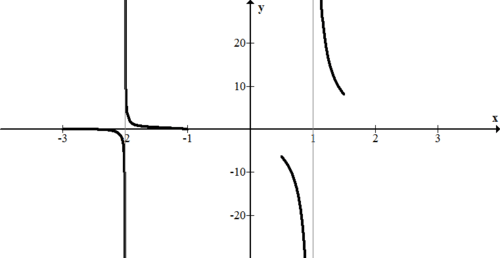 [Figura2]
[Figura2]Crear una función con dos asíntotas verticales en 3 y -2 de tal manera que la función se aproxime al infinito positivo desde ambas direcciones en ambas asíntotas verticales.
Solución
Anteriormente, había una función que se acercaba al infinito negativo desde ambos lados de la asíntota. Esto ocurrió porque el término estaba cuadrado en el denominador. Un término incluso potenciado siempre producirá un término positivo.
\(\ f(x)=\frac{1}{(x-3)^{2}(x+2)^{2}}\)
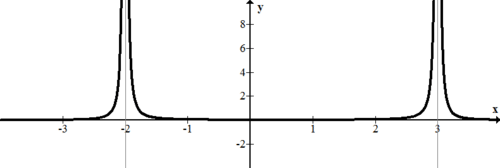 [Figura3]
[Figura3]Crear una función con tres asíntotas verticales de tal manera que la función se aproxime al infinito negativo para valores grandes y pequeños de x y tenga una asíntota oblicua.
Solución
Hay un número infinito de soluciones posibles. La clave es crear una función que pueda funcionar y luego usar el procedimiento de prueba de signos para verificar. Aquí hay una posibilidad.
\(\ f(x)=\frac{-x^{7}}{10(x-1)^{2}(x-2)^{2}(x-4)^{2}}\)
Identificar las asíntotas verticales y utilizar el procedimiento de prueba de señales para esbozar aproximadamente la naturaleza de la función cerca de las asíntotas verticales.
\(\ f(x)=\frac{(x-2)^{3}(x-1)^{2}(x+1)(x+3)}{x^{3}\left(x+\frac{1}{2}\right)(x-1)(x-2)^{2}}\)
Solución
Las asíntotas verticales ocurren en\(\ x=0,-\frac{1}{2}\). Por lo tanto los valores x para firmar son -.001, 0.001, 3.999, 4.0001.
\ (\\ begin {alineado}
f (-0.001) &=+\\
f (0.001) &=-\\
f (3.999) &=-\\
f (4.0001) &=+
\ end {alineado}\)
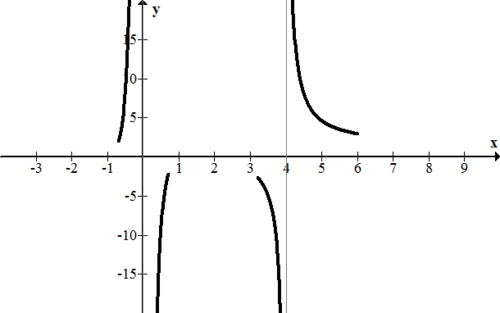 [Figura4]
[Figura4]Revisar
Considera la función a continuación para las preguntas 1-4.
\(\ f(x)=\frac{(x-2)^{4}(x+1)(x+3)}{x^{3}(x+3)(x-4)}\)
- Identificar las asíntotas verticales.
- ¿Esta función tendrá una asíntota oblicua? ¿Una asíntota horizontal? Si es así, ¿dónde?
- ¿Con qué valores necesitarás usar la prueba de signos para ayudarte a hacer un boceto de la gráfica?
- Usa la prueba de signos y dibuja la gráfica cerca de las asíntotas verticales.
Considera la función a continuación para las preguntas 5-8.
\(\ g(x)=\frac{3(x-2)^{2}(x-1)^{2}(x+1)(x+3)}{15 x^{2}(x+5)(x+1)(x-3)^{2}}\)
5. Identificar las asíntotas verticales.
6. ¿Esta función tendrá una asíntota oblicua? ¿Una asíntota horizontal? Si es así, ¿dónde?
7. ¿Con qué valores necesitarás usar la prueba de signos para ayudarte a hacer un boceto de la gráfica?
8. Utilice la prueba de señales y dibuja la gráfica cerca de la asíntota (s) vertical (s).
Considera la función a continuación para las preguntas 9-12.
\(\ h(x)=\frac{9 x^{4}-102 x^{3}+349 x^{2}-340 x+100}{x^{3}-9 x^{2}+24 x-16}\)
9. Identificar las asíntotas verticales.
10. ¿Esta función tendrá una asíntota oblicua? ¿Una asíntota horizontal? Si es así, ¿dónde?
11. ¿Con qué valores necesitarás usar la prueba de signos para ayudarte a hacer un boceto de la gráfica?
12. Usa la prueba de signos y dibuja la gráfica cerca de las asíntotas verticales.
Considera la función a continuación para las preguntas 13-16.
\(\ k(x)=\frac{2 x^{3}-5 x^{2}-11 x-4}{3 x^{3}+11 x^{2}+5 x-3}\)
13. Identificar las asíntotas verticales.
14. ¿Esta función tendrá una asíntota oblicua? ¿Una asíntota horizontal? Si es así, ¿dónde?
15. ¿Con qué valores necesitarás usar la prueba de signos para ayudarte a hacer un boceto de la gráfica?
16. Usa la prueba de signos y dibuja la gráfica cerca de las asíntotas verticales.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.12.
vocabulario
| Término | Definición |
|---|---|
| Comportamiento final | El comportamiento final es una descripción de la tendencia de una función ya que los valores de entrada se vuelven muy grandes o muy pequeños, representados como los 'extremos' de una función gráfica. |
| Asíntota horizontal | Una asíntota horizontal es una línea horizontal que indica dónde se aplana una función ya que la variable independiente se vuelve muy grande o muy pequeña. Una función puede tocar o pasar a través de una asíntota horizontal. |
| Asymptota oblicua | Una asíntota oblicua es una línea diagonal que marca un rango específico de valores hacia los cuales la gráfica de una función puede acercarse, pero generalmente nunca llegar. Existe una asíntota oblicua cuando el numerador de la función es exactamente un grado mayor que el denominador. Una asíntota oblicua se puede encontrar a través de una división larga. |
| Aíntotas oblicuas | Una asíntota oblicua es una línea diagonal que marca un rango específico de valores hacia los cuales la gráfica de una función puede acercarse, pero generalmente nunca llegar. Existe una asíntota oblicua cuando el numerador de la función es exactamente un grado mayor que el denominador. Una asíntota oblicua se puede encontrar a través de una división larga. |
| prueba de señal | La prueba de signos es un procedimiento para determinar únicamente si una función está por encima o por debajo del eje x en un valor x particular. No se calcula la altura específica. |
| Asymptota vertical | Una asíntota vertical es una línea vertical que marca un valor específico hacia el que puede acercarse la gráfica de una función, pero nunca alcanzará. |
Atribuciones de imagen
- [Figura 1]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 2]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 3]
Crédito: Fundación CK-12
Licencia: CC BY-SA - [Figura 4]
Crédito: Fundación CK-12
Licencia: CC BY-SA

