2.5.2: Desigualdades polinomiales y racionales

Última actualización
Guardar como PDF

Page ID: 108722

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Desigualdades polinomiales y racionales

A menudo es más fácil de usar y recordar nuevos términos cuando tienes un 'gancho' o comparación con un término que ya conoces.

“Desigualdad polinómica" es un término generalmente utilizado para referirse a desigualdades donde la variable x tiene un grado de 3 o mayor.

El prefijo “poli” significa 'múltiple' o 'muchos', y la palabra raíz “nomial” significa 'nombre' o 'término'.

Por lo tanto un “polinomio” es literalmente: “muchos términos”.

El prefijo “en” significa 'no', y la palabra raíz “igual” por supuesto significa 'el mismo'.

Por lo tanto y “desigualdad” se refiere a cosas que “no son iguales” o “no iguales”.

¿Puede usar esta lógica para identificar el origen de algunos de los otros términos utilizados en esta lección?

Desigualdades polinomiales y racionales

Desigualdades polinomiales

Resolver desigualdades polinómicas es muy similar a resolver desigualdades cuadráticas. Los pasos básicos son los mismos:

Establecer la desigualdad en la forma p (x) >0 (o p (x) <0, p (x) ≤0, p (x) ≥0)
Encuentra las soluciones a la ecuación p (x) =0.
Divide la línea numérica en intervalos basados en las soluciones a p (x) =0.
Utilice puntos de prueba para encontrar conjuntos de soluciones a la ecuación.

Desigualdades racionales

Hay un paso agregado al proceso de resolución de desigualdades racionales porque una función racional también puede cambiar signos en sus asíntotas verticales o en una ruptura en la gráfica. Por ejemplo, mira la gráfica de la función$\ r(x)=\frac{x}{x^{2}-9}$ a continuación.

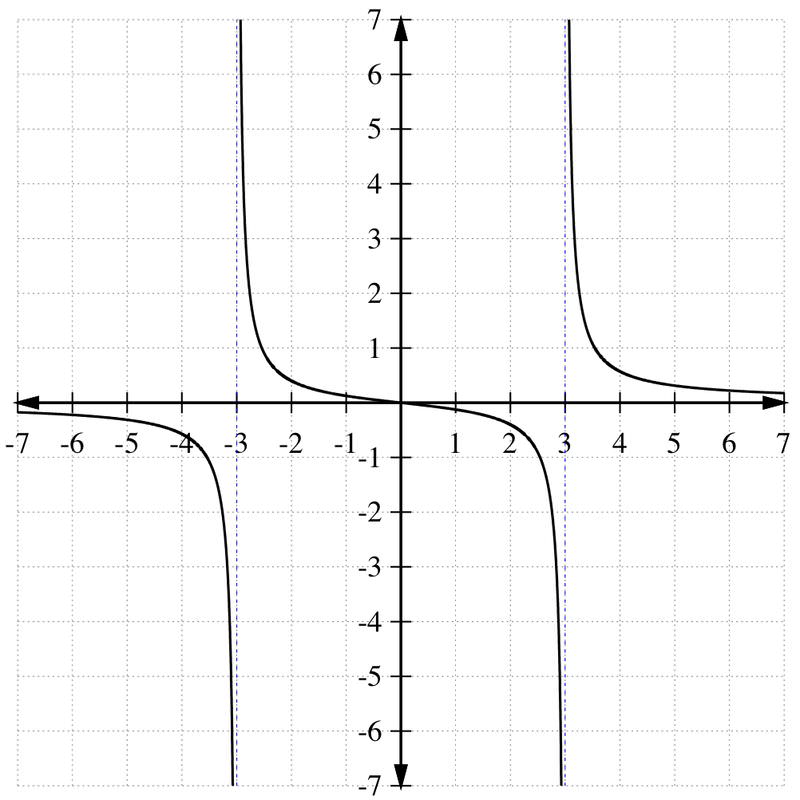
F-D_279E93357D356733DF2549420B5845018D371854CE6064C8184C8AD0+Image_Tiny+Image_Tiny.jpg

Si queremos resolver la desigualdad$\ \frac{x}{x^{2}-9}>0$, entonces necesitamos usar los siguientes puntos críticos: x=0, x=3 y x=−3. x=0 es la solución de establecer el numerador igual a 0, y esto nos da la única raíz de la función. x=±3 son las asíntotas verticales, las x−coordenadas que hacen la función undefined porque poner en 3 o -3 para x provocará una división por cero.

Probando los intervalos entre cada punto crítico para ver si los valores en ese intervalo satisfacen la función nos da:

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
(−∞, −3)	-4	-	no
(-3, 0)	-2	+	si
(0, 3)	2	-	no
(3, +∞)	4	+	si

Así, las soluciones a$\ \frac{x}{x^{2}-9}>0$ son x∈ (−3,0) (3, +∞).

Ejemplos

Ejemplo 1

Anteriormente, se le dio una pregunta sobre la identificación de los orígenes de otros términos en esta lección.

Solución

¿Cuántos de los términos que hemos utilizado recientemente fueron capaces de rastrear los orígenes de? A continuación se listan algunos, ¿encontraste otros?

Bi-nomio: “de dos nombres” o “dos términos” - de “bi”, que significa 'dos' y “nomial”, que significa 'nombre' o 'término'. Cuatrirático: “relacionado con un cuadrado” - de “quadratus”, que significa 'cuadrado'. Ratio-nal: “relacionado con una relación” - de “ratio”, que significa 'razón' (como en “razonar” o “calcular”) y “-al”, que significa “relacionado con”.

Ejemplo 2

Resuelve x ³ −3x ² +2x≥0.

Solución

El polinomio ya está en la forma correcta p (x) ≥0 así resolvemos la ecuación

x ³ −3x ² +2x=0

x (x ² −3x+2) =0

x (x−2) (x−1) =0

Los ceros están en x=0, x=1 y x=2.

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
(−∞ ,0)	-5	-	no
(0, 1)	$\ 1 \over 2$	+	si
(1, 2)	$\ 3 \over 2$	-	no
(2, +∞)	3	+	si

Observe que esta desigualdad es mayor o igual a cero, por lo que incluimos los ceros en el conjunto de soluciones. Por lo tanto, las soluciones son x∈ [0,1] [2, +∞].

Ejemplo 3

Resuelve 6x ⁴ +5x ² <25.

Solución

Primero cambiaremos la desigualdad a 6x ⁴ +5x ² −25<0. Ahora, resuelve la ecuación 6x ⁴ +5x ² −25=0.

6x ⁴ +5x ² −25=0

(3x ² −5) (2x ² +5) =0

El primer término arroja las soluciones$\ x=\pm \sqrt{\frac{5}{3}}$ y no hay soluciones reales para el segundo término.

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
$\ \left(-\infty,-\sqrt{\frac{5}{3}}\right)$	-3	+	no
$\ \left(-\sqrt{\frac{5}{3}}, \sqrt{\frac{5}{3}}\right)$	0	-	si
$\ \left(\sqrt{\frac{5}{3}},+\infty\right)$	3	+	no

Por último, el conjunto de soluciones es$\ x \in\left(-\sqrt{\frac{5}{3}}, \sqrt{\frac{5}{3}}\right)$.

Ejemplo 4

Encuentra el conjunto de soluciones de la desigualdad

$\ \frac{4 x-12}{3 x-2}<0$

Solución

Desde el numerador resolvemos 4x−12=0 o x=3. En el denominador, resolvemos 3x−2=0 y encontramos el punto crítico$\ x=frac{2}{3}$.

Haciendo la mesa

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
$\ \left(-\infty, \frac{2}{3}\right)$	0	+	no
$\ \left(\frac{2}{3}, 3\right)$	1	-	si
(3, +∞)	5	+	no

Por lo tanto, el conjunto de soluciones incluye los números en el intervalo$\ \left(\frac{2}{3}, 3\right)$. O en notación set-builder, la solución es$\ \left\{x \mid \frac{2}{3}<x<3\right\}$.

Ejemplo 5

(usando tecnología) The McNeil Surf Company fabrica trajes de neopreno. Para un número dado de trajes de neopreno x, la ganancia de McNeil, en dólares, viene dada por la función P (x) =−0.01x ² +25x−3000.

Si el gerente de McNeil quiere que la ganancia se mantenga por encima de $9,000, ¿cuál es el número mínimo y máximo de trajes de neopreno que pueden fabricar para mantener ese nivel de ganancia?
¿Cuál es la ganancia máxima que McNeil puede obtener?
¿Puede explicar por qué esta forma podría tener sentido para una función de lucro?

Solución

Establecer la desigualdad
−0.01x ² + 25x − 3000 > 9000

−0.01x ² + 25x − 12000 > 0

Con una calculadora se puede graficar la función Y ₁ = −0.01x ² + 25x − 12000.

En un TI-83: utilice la ventana [−1000,4000] × [−5000,15000].

Los ajustes son:

Xmin=−1000, Xmax=4000, Xscl=500

Ymin=−5000, Ymax=5000, Ysc=1000 xres=1

En un gráfico de software, la imagen se ve así con la ventana x:0→2400 y y:0→3500

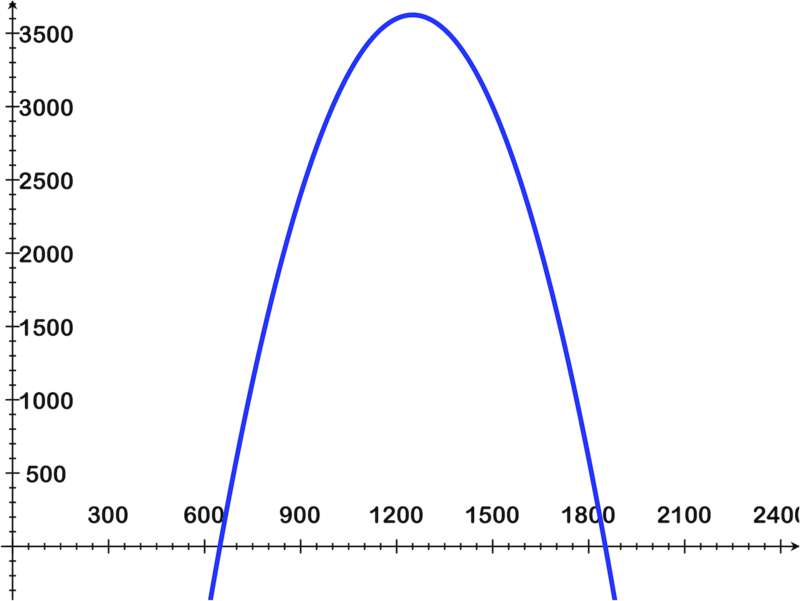
Usando el menú CALC (2ND TRACE), y seleccionando la opción ZEROS, podemos ver que los ceros de Y ₁ =−0.01x ² +25x−12000 están en x=647.920 y x=1852.080.

Al inspeccionar la gráfica, podemos ver que la solución establecida en la desigualdad −0.01x ² +25x−12000>0 es x∈ (648,1852).

Visualmente eso se ve así:
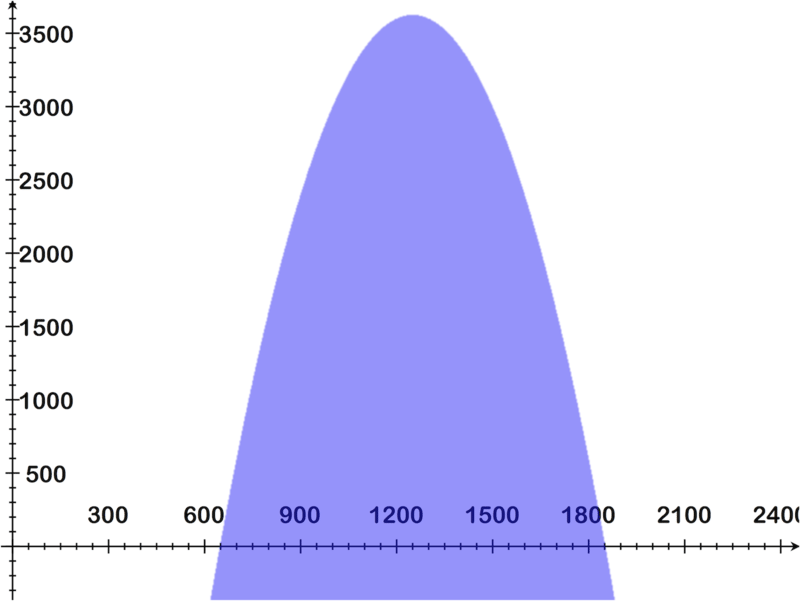
Manteniendo la misma gráfica abierta, utilice CALC MAXIMUM para resolver para obtener el máximo beneficio. El máximo está en (1250, 3625), lo que indica que la ganancia máxima es de $3625 por encima del mínimo que fijamos: de $9000.
Por lo que la ganancia máxima real es de $12,625 cuando se producen 1250 trajes de neopreno.
Una posible razón por la que la función de ganancia podría tomar esta forma son los costos laborales. Si McNeil quiere hacer una gran cantidad de trajes de neopreno en un corto periodo de tiempo, entonces eso puede requerir pagar horas extras para los trabajadores, y esto podría reducir el margen de ganancia.

Ejemplo 6

Para la siguiente función racional, determinar las limitaciones en el dominio y las asíntotas, y luego bosquejar la gráfica.

$\ f(x) \geq \frac{2 x+5}{x-1}$

Solución

Para identificar la gráfica de la desigualdad$\ f(x) \geq \frac{2 x+5}{x-1}$, primero trátela como si fuera la igualdad$\ f(x) \geq \frac{2 x+5}{x-1}$

Para$\ f(x) \geq \frac{2 x+5}{x-1}$:

Para encontrar los puntos críticos, identifique el (los) valor (s) que hacen que el denominador = 0: x≠ 1

Eso nos da una asíntota vertical de x=1

La asíntota horizontal se hace evidente a medida que x se vuelve verdaderamente enorme y los “+5" y “-1" ya no importan. En ese punto, tenemos$\ f(x)=\frac{2 x}{x} \rightarrow f(x)=2$ Así que la asíntota horizontal es y=2

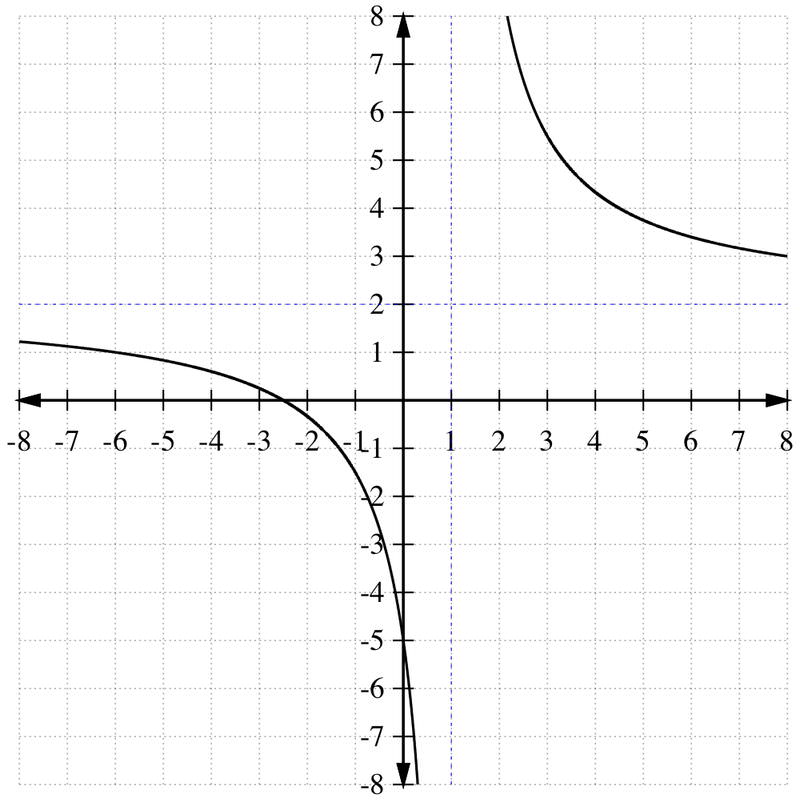
f-d_27a70869ffdce173a36513ac8bcdec45a942110c360f1273150d201b+image_tiny+image_tiny.jpg

Ahora que conoces la forma de la gráfica, simplemente sombrea el área por encima de las líneas, ya que la función original era f (x) es mayor que la función, y deja las líneas sólidas ya que era una mayor que o igual a.

La gráfica final debería tener el siguiente aspecto:

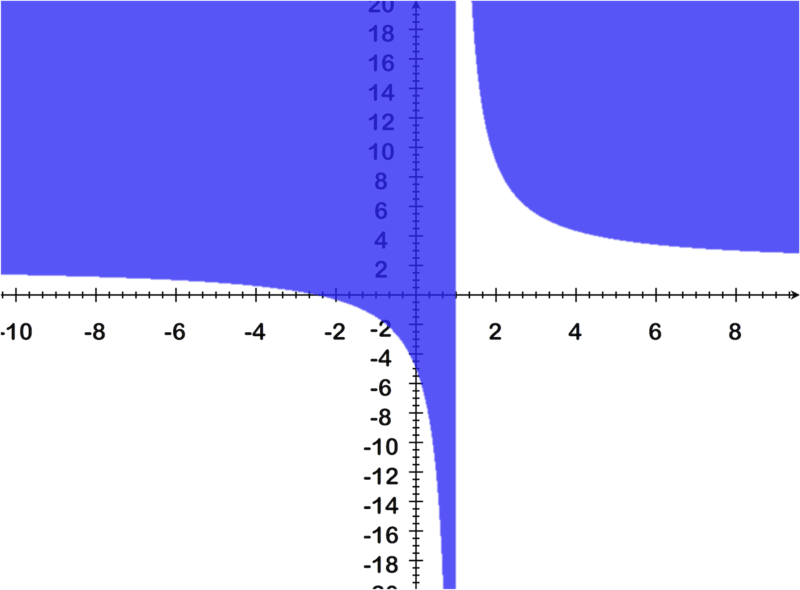
f-d_28719d5fdcc6717815e40d768766fb59ce1fc4a268785eb088c845b+image_tiny+imagen_tiny.png

Revisar

Encuentre el conjunto de soluciones de las siguientes desigualdades sin usar una calculadora. Muestre el conjunto de soluciones en una línea numérica.

x ² + 2x − 3 ≤ 0
3x ² − 7x + 2 > 0
−6x ² − 13x + 5 ≥ 0
$\ \frac{5 x-1}{x-2}>0$
$\ \frac{1-x}{x}<1$
Resolver: 4x ³ −4x ² −3x>0
Resolver:$\ \frac{x^{4}}{4}-x^{2}<0$
Resolver: 4x ³ − 8x ² − x + 2 ≥ 0
$\ \frac{n^{3}-2 n^{2}-n+2}{n^{3}+3 n^{2}+4 n+12}<0$
$\ \frac{n^{3}+3 n^{2}-4 n-12}{n^{3}-5 n^{2}+4 n-20} \leq 0$
$\ \frac{2 n^{3}+5 n^{2}-18 n-45}{3 n^{3}-n^{2}+27 n-9} \geq 0$
$\ \frac{12 n^{3}+16 n^{2}-3 n-4}{8 n^{3}+12 n^{2}+10 n+15}>0$

Utilice una calculadora para resolver las siguientes desigualdades. Redondea tu respuesta a tres lugares después del decimal.

−9.8t ² + 357.6t ≥ 0
x ³ − 5x + 7 ≤ −4x ² + 18
$\ \frac{x^{2}-2 x}{x-5}>x^{2}-25$
Resolver y graficar:$\ f(x)>\frac{9 x^{2}-4}{3 x+2}$
La resistencia total de dos componentes electrónicos cableados en paralelo viene dada por$\ \frac{R_{1} R_{2}}{R_{1}+R_{2}}$ donde _R1 y _R2 son las resistencias individuales (en Ohmios) de los dos componentes. a) Si la resistencia de _R1 es de 20 Ohmios, cuál es la resistencia máxima de R ₂ si la la resistencia total debe ser inferior a 15 Ohmios? b) ¿Cuál es la resistencia teórica máxima de este circuito? ¿Cómo lo sabes?
Un lote rectangular de terreno tiene una longitud que es de 7 metros más del doble de su ancho. Si el área del lote es mayor a 60 metros cuadrados, ¿cuáles son los posibles valores de los anchos del lote?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.10.

El vocabulario

Término	Definición
dominio	El dominio de una función es el conjunto de valores x para los que se define la función.
Desigualdad polinómica	El término desigualdad polinómica se utiliza generalmente para describir una desigualdad con un coeficiente x término de tres o mayor.
desigualdad cuadrática	Una desigualdad cuadrática es una expresión cuadrática que se especifica para ser mayor o menor que un valor dado.
Función Racional	Una función racional es cualquier función que pueda escribirse como la relación de dos funciones polinómicas.
Desigualdad Racional	Una desigualdad racional es una relación de dos polinomios, especificados para ser mayor o menor que un valor dado.
Asíntota vertical	Una asíntota vertical es una línea vertical que marca un valor específico hacia el que puede acercarse la gráfica de una función, pero nunca alcanzará.

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
(−∞ ,0)	-5	-	no
(0, 1)	\(\ 1 \over 2\)	+	si
(1, 2)	\(\ 3 \over 2\)	-	no
(2, +∞)	3	+	si

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
\(\ \left(-\infty,-\sqrt{\frac{5}{3}}\right)\)	-3	+	no
\(\ \left(-\sqrt{\frac{5}{3}}, \sqrt{\frac{5}{3}}\right)\)	0	-	si
\(\ \left(\sqrt{\frac{5}{3}},+\infty\right)\)	3	+	no

Intervalo	Punto de prueba	¿Positivo/Negativo?	¿Parte del conjunto de soluciones?
\(\ \left(-\infty, \frac{2}{3}\right)\)	0	+	no
\(\ \left(\frac{2}{3}, 3\right)\)	1	-	si
(3, +∞)	5	+	no