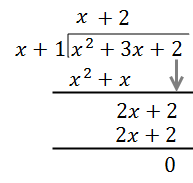2.6.1: División Larga de Polinomios

Última actualización
Guardar como PDF

Page ID: 108647

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

División Larga y División Sintética

¿Se pueden dividir los siguientes polinomios?

\(\ \frac{x^{2}-5 x+6}{x-2}\)

División Larga y División Sintética

Polinomio División Larga

Siempre que quieras dividir un polinomio por un polinomio, puedes usar un proceso llamado polinomio división larga. Este proceso es similar a la división larga para números regulares. Mira el problema a continuación:

\(\ \frac{\left(x^{2}+3 x+2\right)}{(x+1)}\)

Esto es lo mismo que el problema de división a continuación:

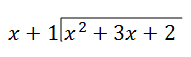
F-d_514f0f506c20ad0916f4b6d8b92dc800f7b50f37c7062f8f5369a3c4+imagen_tiny+imagen_tiny.png

Paso 1: Divide el primer término en el numerador (x ²) por el primer término en el denominador (x). Pon este resultado por encima de la barra de división en tu respuesta. En este caso,\(\ \frac{x^{2}}{x}=x\).

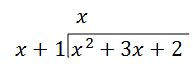
f-d_04c47d5c17bab8c46f5a87659c805522857a8ce241e1ac06c25c47e7+image_tiny+imagen_tiny.png

Paso 2: Multiplica el denominador (x+1) por el resultado del Paso 1 (x), y pon el nuevo resultado debajo de tu numerador. Entonces, resta para obtener tu nuevo polinomio. ¡Este es el mismo proceso que en la división larga de número regular!

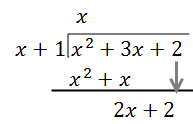
f-d_d1d39546d223a6d1667765a8cae7848cb6333772a056822a1e460de2+image_tiny+image_tiny.png

Paso 3: Dividir el primer término en el nuevo polinomio (2x) por el primer término en el denominador (x). Pon este resultado por encima de la barra de división en tu respuesta. Multiplica, resta y repite este proceso hasta que ya no puedas repetirlo.

Por lo tanto:\(\ \frac{\left(x^{2}+3 x+2\right)}{(x+1)}=(x+2)\)

División Sintética

La división sintética es otro método de división de polinomios. Se trata de una taquigrafía de división larga que sólo funciona cuando se está dividiendo por un polinomio de grado 1. Por lo general, el divisor está en la forma (x±a). En la división sintética, a diferencia de la división larga, sólo te preocupan los coeficientes en los polinomios. Considere el mismo problema que el anterior:

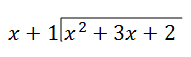F-d_514f0f506c20ad0916f4b6d8b92dc800f7b50f37c7062f8f5369a3c4+imagen_tiny+imagen_tiny.png

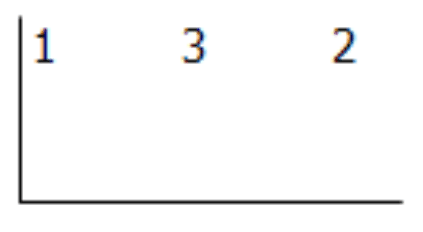
Paso 1: Escribe los coeficientes en un signo de división al revés.

f-d_673fbc23f79722f395795c50462e8245f0a8d1aef56a464444d7ad78+image_tiny+image_tiny.png

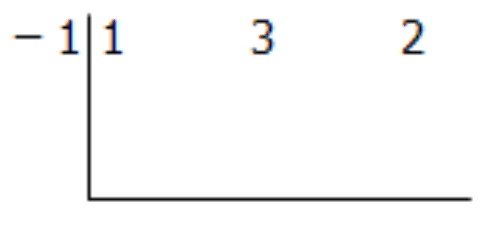
Paso 2: Ponga lo contrario del número del divisor a la izquierda del símbolo de división. En este caso, el divisor es x+1, por lo que usarás un −1.

f-d_79055d60db9659bd43145a43c8e339da74f47d25770ef1f313926a38+image_tiny+image_tiny+image_tiny.png

Paso 3: Toma tu coeficiente inicial y bájalo por debajo del símbolo de división.

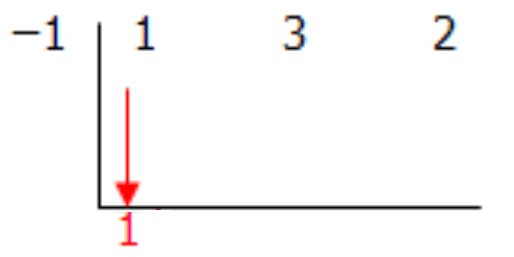f-d_ce9450e8c5098a25b1c2bc43a8e9c1d05752bf34d902d314f66dafcc+image_tiny+image_tiny.png

Paso 4: Multiplique este número por el número a la izquierda del símbolo de división y colóquelo en la siguiente columna. Sumar los dos números juntos y colocar este nuevo número debajo del signo de división.

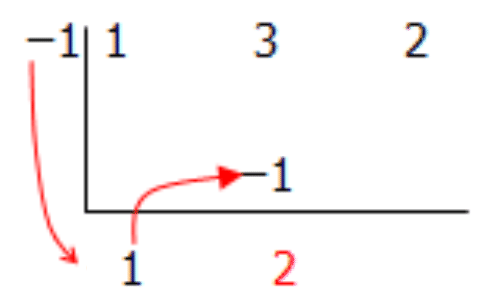F-D_6E63383E009344F7034DBF47176B190B954E5EE312497AB9AA692214+Image_Tiny+Image_Tiny.png

Paso 5: Multiplique este segundo número por el número a la izquierda del símbolo de división y colóquelo en la tercera columna. Sumar los dos números juntos y colocar este nuevo número debajo del signo de división.

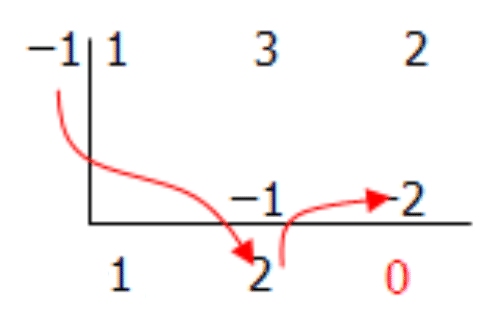f-d_02bc84fbae4e2f0f1a8a8fcb9c7dd5f84fdfb855b373c8186ec494b6+image_tiny+image_tiny.png

Los números debajo del signo de división representan tus coeficientes. Por lo tanto,

\(\ \frac{\left(x^{2}+3 x+2\right)}{(x+1)}=(x+2)\)

Ejemplos

Ejemplo 1

Anteriormente, se le pidió dividir polinomios:

\(\ \frac{x^{2}-5 x+6}{x-2}\)

Solución

Se puede utilizar división larga o división sintética.

División Larga:

Paso 1: Divide el primer término en el numerador por el primer término en el denominador, pon esto en tu respuesta. Por lo tanto\(\ \frac{x^{2}}{x}=x\).

\ (\\ begin {array} {c}
\ textcolor {rojo} x\\
(x-2) |\ overline {x^2 -5x + 6}
\ end {array}\)

Paso 2: Multiplica el denominador por este número (variable) y ponlo debajo de tu numerador, resta y obtén tu nuevo polinomio.

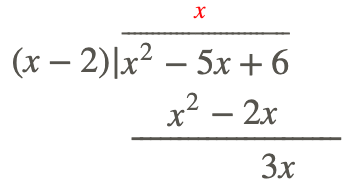
Screen Shot 2021-01-18 a las 9.20.54 PM.png

Paso 3: Repite el proceso hasta que ya no puedas repetirlo.

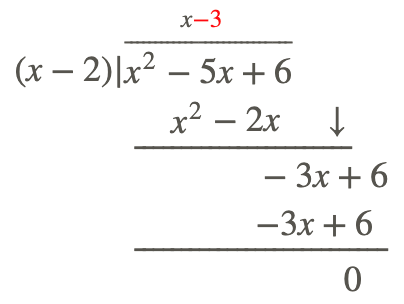
Screen Shot 2021-01-18 a las 9.21.37 PM.png

Por lo tanto:\(\ \frac{x^{2}-5 x+6}{x-2}=(x-3)\)

Ejemplo 2

Utilice la división larga para dividir:

\(\ \frac{x^{2}+6 x-7}{x-1}\)

Solución

Paso 1: Divide el primer término en el numerador por el primer término en el denominador, pon esto en tu respuesta. Por lo tanto\(\ \frac{x^{2}}{x}=x\).

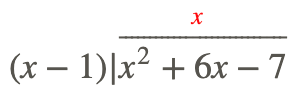
Screen Shot 2021-01-18 a las 9.26.30 PM.png

Paso 2: Multiplica el denominador por este número (variable) y ponlo debajo de tu numerador, resta y obtén tu nuevo polinomio.

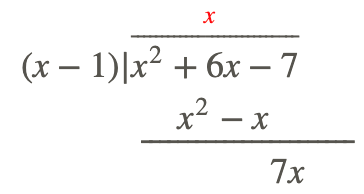
Screen Shot 2021-01-18 a las 9.27.12 PM.png

Paso 3: Repite el proceso hasta que ya no puedas repetirlo.

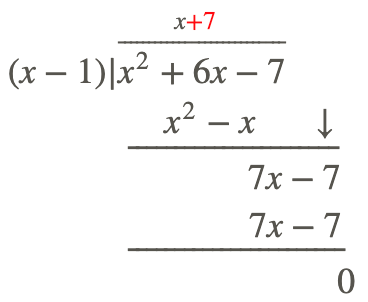
Screen Shot 2021-01-18 a las 9.27.46 PM.png

Por lo tanto:\(\ \frac{x^{2}+6 x-7}{x-1}=(x+7)\)

Ejemplo 3

Utilice la división larga para dividir:

\(\ \frac{2 x^{2}+7 x+5}{2 x+5}\)

Solución

Paso 1: Divide el primer término en el numerador por el primer término en el denominador; pon esto en tu respuesta. Por lo tanto\(\ \frac{2 x^{2}}{2 x}=x\).

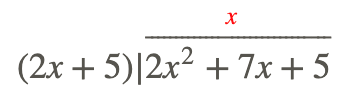
Screen Shot 2021-01-18 a las 9.34.32 PM.png

Paso 2: Multiplica el denominador por este número (variable) y ponlo debajo de tu numerador, resta y obtén tu nuevo polinomio.

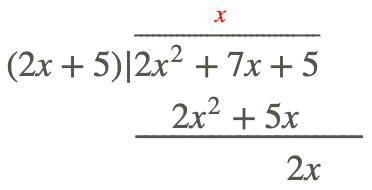
Screen Shot 2021-01-18 a las 9.35.36 PM.png

Paso 3: Repite el proceso hasta que ya no puedas repetirlo.

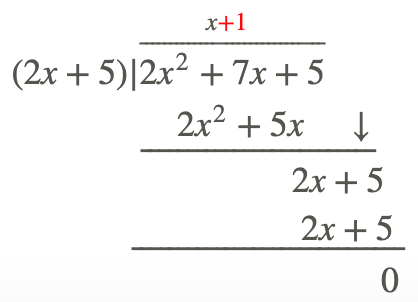
Screen Shot 2021-01-18 a las 9.36.33 PM.png

Por lo tanto:\(\ \frac{2 x^{2}+7 x+5}{2 x+5}=(x+1)\)

Ejemplo 4

Usa división sintética para dividir:

\(\ \frac{3 x^{2}+x-4}{x-1}\)

Solución

Paso 1: Escribe los coeficientes en un signo de división al revés.

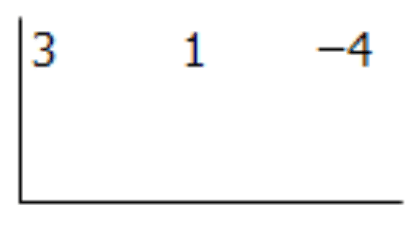
f-d_0ff01d5252c846f566fff615a81cc2c11a113ea7017b82d2f8877970+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

Paso 2: Ponga lo contrario del número del divisor a la izquierda del símbolo de división.

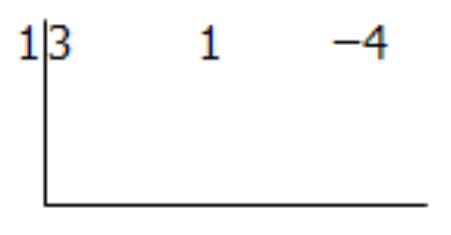
f-d_900e5931238f2ddd61b31077faa64a0b468e00849d921a53de45a8ad+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

Paso 3: Toma tu coeficiente inicial y bájalo por debajo del símbolo de división.

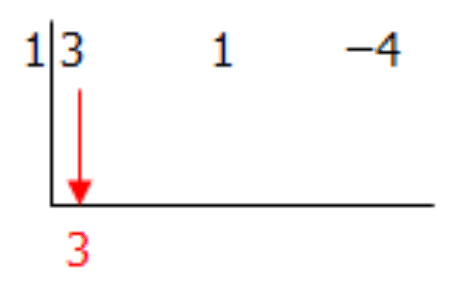
f-d_ee0a2bb1208c88acd667806ffe005fc67b42003027492a3638ff5e4c+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

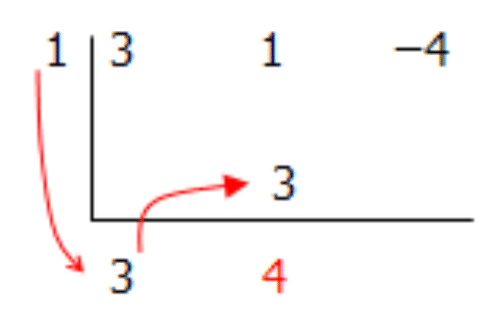
F-d_35902179b39a44c2b1989ff6a361c1905f0bcbede772d08920ec85bc+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

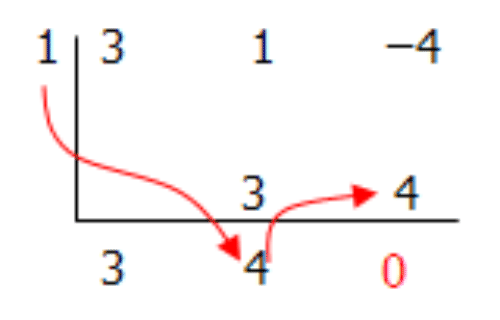
f-d_1eace6276bd4c484cddba64322ebc7d03cd4137310c8ea6992500171+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

Por lo tanto:\(\ \frac{3 x^{2}+x-4}{x-1}=(3 x+4)\)

Revisar

Utilice la división larga para dividir cada uno de los siguientes:

(x ² +7x+12) ÷ (x+3)
(x ² +4x+3) ÷ (x+3)
(a ² −4a−45) ÷ (a−9)
(3x ² +5x−2) ÷ (3x−1)
(2x ² −5x+2) ÷ (2x−1)

Use división sintética para dividir cada uno de los siguientes:

(b ² −5b+6) ÷ (b−3)
(x ² −6x+8) ÷ (x−4)
(a ² −1) ÷ (a+1)
(c ² −9) ÷ (c−3)
(5r ² +2r−3) ÷ (r+1)

Divida cada uno de los siguientes:

\(\ \frac{2 x^{3}-7 x^{2}-14 x-5}{x-5}\)
\(\ \frac{9 x^{4}-15 x^{3}+12 x^{2}-11 x-15}{3 x^{3}+4 x+3}\)
\(\ \frac{6 x^{4}+4 x^{3}+9 x^{2}+2 x+3}{2 x^{2}+1}\)
\(\ \frac{x^{4}+4 x^{3}+3 x^{2}+x+1}{x+1}\)
\(\ \frac{2 x^{3}+7 x^{2}-27 x+18}{x+6}\)
\(\ \frac{8 x^{3}-2 x^{2}+7 x+5}{2 x+1}\)
\(\ \frac{3 x^{3}-15 x^{2}+4 x-20}{x-5}\)
\(\ \frac{9 x^{3}+26 x^{2}-48 x+5}{x^{2}+3 x-5}\)
\(\ \frac{-x^{3}+13 x+12}{x+3}\)
\(\ \frac{x^{3}-2 x^{2}-5 x+10}{x-2}\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.13.

El vocabulario

Término	Definición
Dividendo	En un problema de división, el dividendo es el número o expresión que se está dividiendo.
divisor	En un problema de división, el divisor es el número o expresión que se está dividiendo en el dividendo. Por ejemplo: En la expresión 152÷6, 6 es el divisor y 152 es el dividendo.

Atribuciones de imagen

[Figura 1]
Fuente: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figura 2]
Fuente: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figura 3]
Fuente: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figura 4]
Fuente: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figura 5]
Fuente: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG
[Figura 6]
Fuente: https://commons.wikimedia.org/wiki/File:Computer_in_tuition_centre.JPG

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejemplo 4