3.5.2: Modelos logarítmicos
- Page ID
- 108535
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Modelos logarítmicos
En lecciones anteriores, se utilizó un modelo exponencial para predecir la población de un pueblo con base en una tasa de crecimiento constante como 6% anual.
Sin embargo, en el mundo real, las poblaciones a menudo no solo crecen de manera continua y sin límite. Un pueblo originalmente fundado cerca de una fuente de agua conveniente puede crecer muy rápidamente al principio, pero la expansión se ralentizará drásticamente a medida que las casas y los negocios se queden sin espacio cerca de la fuente de agua y necesiten comenzar a transportar agua cada vez más lejos.
¿Cómo se puede modelar una situación como esta con una ecuación?
Modelos logarítmicos
En una lección previa, consideramos las soluciones de ecuaciones logarítmicas simples. Ahora volvemos a ese tema y exploramos algunos ejemplos más complejos. Resolver ecuaciones logarítmicas más complicadas puede ser menos difícil de lo que piensas, al usar nuestro conocimiento de las propiedades de los registros.
Por ejemplo, considere la ecuación log 2 (x) + log 2 (x - 2) = 3. Podemos resolver esta ecuación usando una propiedad logarítmica.
| log 2 (x) + log 2 (x - 2) = 3 | |
|---|---|
| log 2 (x (x - 2)) = 3 | log b x + log b y = log b (xy) |
| tronco 2 (x 2 - 2 x) = 3 ⇒ | escribir la ecuación en forma exponencial. |
| 2 3 = x 2 - 2 x | |
| x 2 - 2 x - 8 = 0 | Resolver la cuadrática resultante |
| (x - 4) (x + 2) = 0 | |
| x = -2, 4 |
La cuadrática resultante tiene dos soluciones. Sin embargo, solo x = 4 es una solución a nuestra ecuación original, ya que log 2 (-2) no está definido. Nos referimos a x = -2 como una solución ajena.
Ejemplos
Anteriormente, se le preguntó cómo se podía modelar una situación con una ecuación.
Solución
Una población que aumenta continuamente a un ritmo constante puede modelarse con una función exponencial.
Una población que aumenta rápidamente y luego se nivela puede modelarse con una función logarítmica.
Resuelve cada ecuación.
- log (x + 2) + log 3 = 2
- ln (x + 2) - ln (x) = 1
Solución
-
log (3 (x + 2)) = 2 log b x + log b y = log b (xy) tronco (3 x + 6) = 2 Simplificar la expresión 3 (x +2) 10 2 = 3 x + 6 Escribir la expresión logarítmica en forma exponencial 100 = 3 x + 6 3 x = 94 Resolver la ecuación lineal x = 94/3 -
\(\ \ln \left(\frac{x+2}{x}\right)=1\) \(\ \log _{b} x-\log _{b} y=\log _{b}\left(\frac{x}{y}\right)\) \(\ e^{1}=\frac{x+2}{x}\) Escribe la expresión logarítmica en forma exponencial. ex=x+2 Multiplica ambos lados por x. ex−x=2 Factor de salida x. x (e−1) =2 Aislar x. \(\ x=\frac{2}{e-1}\) La solución anterior es una solución exacta. Si queremos una aproximación decimal, podemos usar una calculadora para encontrar esa x ≈ 1.16. También podemos usar una calculadora gráfica para encontrar una solución aproximada. Consideremos nuevamente la ecuación ln (x + 2) - ln (x) = 1. Podemos resolver esta ecuación resolviendo un sistema:
\ (\\ izquierda\ {\ begin {array} {l}
y=\ ln (x+2) -\ ln (x)\\
y=1
\ end {array}\ right.\)Si graficas el sistema en tu calculadora gráfica, deberías ver que la curva y la línea horizontal se cruzan en un punto. Usando la función INTERSECT en el menú CALC (presione <2nd>[CALC]), debe encontrar que la coordenada x del punto de intersección es aproximadamente 1.16. Este método te permitirá encontrar soluciones aproximadas para ecuaciones logarítmicas más complicadas.
Utilice una calculadora gráfica para resolver cada ecuación:
- tronco (5 - x) + 1 = log x
- log 2 (3 x + 8) + 1 = log 3 (10 - x)
Solución
- Las gráficas de y = log (5 - x) + 1 e y = log x se cruzan en x ≈ 4.5454545.
Por lo tanto, la solución de la ecuación es x ≈ 4.54.
- Primero, para graficar las ecuaciones, debes reescribirlas en términos de un logaritmo común o un logaritmo natural. Las ecuaciones resultantes son:\(\ y=\frac{\log (3 x+8)}{\log 2}+1 \text { and } y=\frac{\log (10-x)}{\log 3}\) Las gráficas de estas funciones se cruzan en x ≈ -1.87. Este valor es la solución aproximada a la ecuación.
Considere el crecimiento de la población:
| Año | Población |
|---|---|
| 1 | 2000 |
| 5 | 4200 |
| 10 | 6500 |
| 20 | 8800 |
| 30 | 10500 |
| 40 | 12500 |
Solución
Si trazamos estos datos, vemos que el crecimiento no es del todo lineal, y tampoco es exponencial.
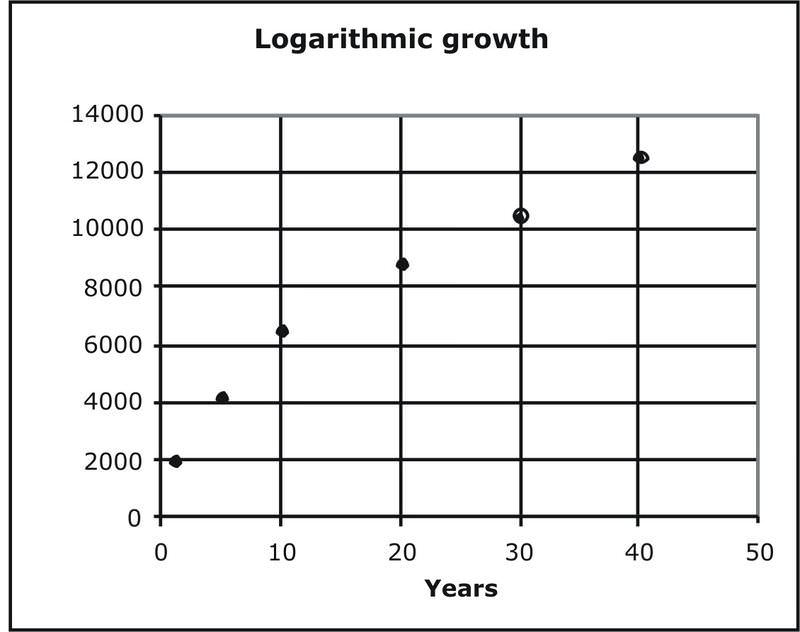
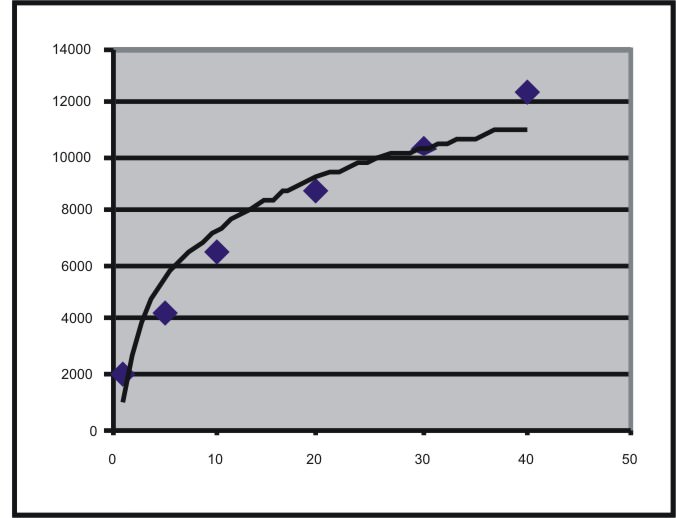
Podemos encontrar una función logarítmica para modelar estos datos. Primero ingrese los datos en la tabla en L1 y L2. Después presiona STAT para llegar al menú CALC. Esta vez elige la opción 9. Debe obtener la función y = 930.4954615 + 2780.218173 ln x Si ve la gráfica y los puntos de datos juntos, como se describe en la Nota de Tecnología anterior, verá que la gráfica de la función no toca los puntos de datos, sino que modela la tendencia general de los datos.
Nota sobre la tecnología: también puedes hacerlo usando una hoja de cálculo de Excel. Introduzca los datos en una hoja de trabajo y cree un diagrama de dispersión insertando un gráfico. Después de crear el gráfico, desde el menú del gráfico, elija “agregar línea de tendencia”. Entonces podrás elegir el tipo de función. Tenga en cuenta que si desea utilizar una función logarítmica, el dominio de su conjunto de datos debe ser números positivos. El menú del gráfico en realidad no le permitirá elegir una línea de tendencia logarítmica si sus datos incluyen valores de x cero o negativos. Ver abajo:
Resolver para x: log2x−log2 (x−4) =12.
Solución
Para resolver log 2 x−log 2 (x−4) =12:
\(\ \log _{2} \frac{x}{x-4}=12\): Usando\(\ \log _{x} y-\log _{x} z=\log _{x} \frac{y}{z}\)
\(\ 2^{12}=\frac{x}{x-4}\): Escribir en forma exponencial
\(\ 4,096=\frac{x}{x-4}\): Con una calculadora
4,096x−16384=x: Multiplica ambos lados por x−4
4.095x=16.384: Simplificar
x=4: Dividir
Los biólogos utilizan la fórmula N=kloga para estimar el número de especies n que viven en un área dada A multiplicando por una constante k que cambia por ubicación. Si un bosque lluvioso en particular tiene una k constante de 943 ¿cuántas especies se estimarían para vivir en una superficie de 950km 2?
Solución
Para encontrar el número de especies en una superficie de 950km 2:
n=943log950: Sustituir los valores de k y A dados
n=9432.977: Con calculadora
n=2,807
Por lo tanto, 2.807 especies probablemente vivirían en la zona.
Revisar
Expresar 1-7 en forma exponencial:
- \(\ \log _{12} \frac{1}{1728}=-3\)
- \(\ \log _{216} 6=\frac{1}{3}\)
- \(\ \log _{\frac{1}{3}} \frac{1}{9}=3\)
- \(\ \log _{\frac{1}{4}} \frac{1}{16}=2\)
- \(\ \log _{5} 125=3\)
- \(\ \log _{15} 225=2\)
- \(\ \log _{25} 5=\frac{1}{2}\)
Para preguntas 8-13, resolver para x.
- \(\ \log _{x} 64=2\)
- \(\ \log _{3} 6561=x\)
- \(\ \log _{5} x=4\)
- \(\ \log _{x} 27=3\)
- \(\ \log _{2} x=6\)
- \(\ \log _{4} 64=x\)
Para preguntas 14-19, resolver para x.
- \(\ 4 \log \left(\frac{x}{5}\right)+\log \left(\frac{625}{4}\right)=2 \log x\)
- \(\ \log _{5} z+\frac{\log _{5} 125}{\log _{5} x}=\frac{7}{2}\)
- \(\ \log p=\frac{2-\log p}{\log p}\)
- \(\ 2\log x−2\log (x+1)=0\)
- \(\ \log(25−z^3)−3\log(4−z)=0\)
- \(\ \frac{\log \left(35-y^{3}\right)}{\log (5-y)}=3\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 3.10.
vocabulario
| Término | Definición |
|---|---|
| Tronco Común | Un logaritmo común es un logaritmo con base 10. El registro suele escribirse sin la base. |
| Logaritmo Común | Un logaritmo común es un logaritmo con base 10. El registro suele escribirse sin la base. |
| modelo exponencial | Un modelo exponencial es una función que refleja una cantidad que crece o decae a una tasa proporcional a su valor actual. |
| Solución Extrana | Una solución ajena es una solución de una versión simplificada de una ecuación original que, cuando se comprueba en la ecuación original, en realidad no es una solución. |
| Funciones logarítmicas | Las funciones logarítmicas son las inversas de las funciones exponenciales. Recordemos que log b n=a es equivalente a b a =n. |
| Tronco Natural | Un logaritmo natural es un logaritmo con base e. El logaritmo natural se escribe como ln. |
| Logaritmo Natural | Un logaritmo natural es un logaritmo con base e. El logaritmo natural se escribe como ln. |