4.5.2: Números Complejos
- Page ID
- 108372
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Definición de números complejos
La temperatura más fría posible, conocida como cero absoluto, es de casi —460 grados Fahrenheit. ¿Cuál es la raíz cuadrada de este número?
Números Complejos
Antes de este concepto, todos los números han sido números reales. \(\ 2,-5, \sqrt{11}\), y\(\ \frac{1}{3}\) son todos ejemplos de números reales. Con lo que hemos aprendido anteriormente, no podemos encontrar\(\ \sqrt{-25}\) porque no se puede tomar la raíz cuadrada de un número negativo. No hay un número real que, al multiplicarse por sí mismo, sea igual a -25. Vamos a simplificar\(\ \sqrt{-25}\).
\(\ \sqrt{-25}=\sqrt{25 \cdot-1}=5 \sqrt{-1}\)
Para tomar la raíz cuadrada de un número negativo vamos a asignar\(\ \sqrt{-1}\) una variable,\(\ i. i\) representa un número imaginario. Ahora, podemos usar i para tomar la raíz cuadrada de un número negativo.
\(\ \sqrt{-25}=\sqrt{25 \cdot-1}=5 \sqrt{-1}=5 i\)
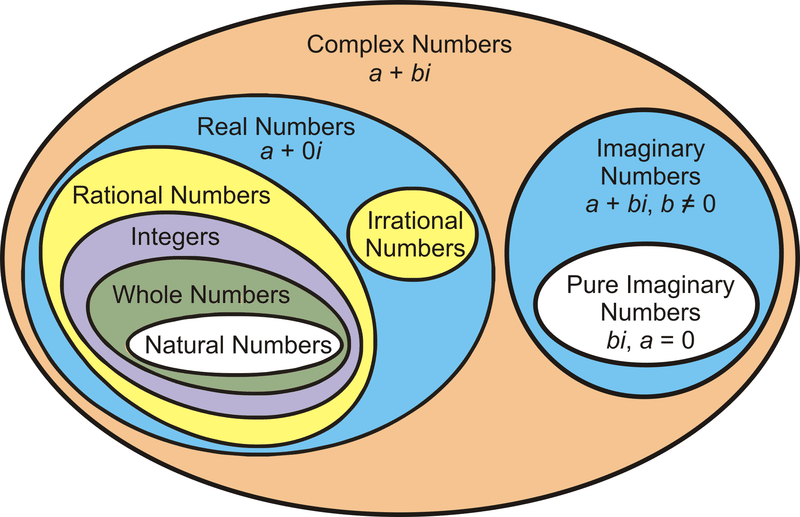
Todos los números complejos tienen la forma a+bi, donde a y b son números reales. a es la parte real del número complejo y b es la parte imaginaria. Si b=0, entonces se deja a la izquierda y el número es un número real. Si a=0, entonces el número es solo bi y se llama un número imaginario puro. Si b≠ 0 y a≠ 0, el número será un número imaginario.
[Figura1]Vamos a encontrar\(\ \sqrt{-162}\).
Primero saque el\(\ i\). Entonces, simplifique\(\ \sqrt{162}\).
\(\ \sqrt{-162}=\sqrt{-1} \cdot \sqrt{162}=i \sqrt{162}=i \sqrt{81 \cdot 2}=9 i \sqrt{2}\)
Poderes de i
Además de poder ahora tomar la raíz cuadrada de un número negativo, i también tiene algunas propiedades interesantes. Intenta encontrar\(\ i^{2}, i^{3}, \text { and } i^{4}\).
Paso 1: Escriba\(\ i^{2}\) y simplifique. \(\ i^{2}=i \cdot i=\sqrt{-1} \cdot \sqrt{-1}=\sqrt{-1}^{2}=-1\)
Paso 2: Escriba\(\ i^{3}\) y simplifique. \(\ i^{3}=i^{2} \cdot i=-1 \cdot i=-i\)
Paso 3: Escriba\(\ i^{4}\) y simplifique. \(\ i^{4}=i^{2} \cdot i^{2}=-1 \cdot-1=1\)
Paso 4: Escriba\(\ i^{5}\) y simplifique. \(\ i^{5}=i^{4} \cdot i=1 \cdot i=i\)
Paso 5: Escribe\(\ i^{6}\) y simplifica. \(\ i^{6}=i^{4} \cdot i^{2}=1 \cdot-1=-1\)
Paso 6: ¿Ves un patrón? Descríbelo y trate de encontrar\(\ i^{19}\).
Deberías ver que los poderes de\(\ i\) repetir cada 4 poderes. Entonces, todos los poderes que son divisibles por 4 serán iguales a 1. Para encontrar\(\ i^{19}\), divida 19 por 4 y determinar el resto. Eso te dirá de qué poder es lo mismo que.
\(\ i^{19}=i^{16} \cdot i^{3}=1 \cdot i^{3}=-i\)
Ahora, encontremos los siguientes poderes de i.
- \(\ i^{32}\)
32 es divisible por 4, entonces\(\ i^{32}=1\).
- \(\ i^{50}\)
50÷4=12, con un resto de 2. Por lo tanto,\(\ i^{50}=i^{2}=-1\).
- \(\ i^{7}\)
7÷4=1, con un resto de 3. Por lo tanto,\(\ i^{7}=i^{3}=-i\)
Por último, simplifiquemos las siguientes expresiones complejas.
- \(\ (6-4 i)+(5+8 i)\)
\(\ (6-4 i)+(5+8 i)={\color{red}{6}}{\color{blue}-4 i}+{\color{red}5}+{\color{blue}8 i}={\color{red}11}+\color{blue}4 i\)
- \(\ 9−(4+i)+(2−7i)\)
\(\ 9-(4+i)+(2-7 i)={\color{red}9-4}{\color{blue}-i}+{\color{red}2}{\color{blue}-7 i}={\color{red}7}\color{blue}-8 i\)
Para sumar o restar números complejos, es necesario combinar términos similares. Ten cuidado con los negativos y distribuirlos adecuadamente. Tu respuesta siempre debe ser en forma estándar, que es\(\ a+bi\).
Ejemplos
Antes, se le pidió que encontrara la raíz cuadrada de -460 grados.
Solución
Estamos buscando\(\ \sqrt{-460}\).
Primero tenemos que sacar el\(\ i\). Entonces, tenemos que simplificar\(\ \sqrt{460}\).
\(\ \sqrt{-460}=\sqrt{-1} \cdot \sqrt{460}=i \sqrt{460}=i \sqrt{4 \cdot 115}=2 i \sqrt{115}\)
Simplificar\(\ \sqrt{-49}\).
Solución
Reescribir\(\ \sqrt{-49}\) en términos de lo radical\(\ i\) y simplificar.
\(\ \sqrt{-49}=i \sqrt{49}=7 i\)
Simplificar\(\ \sqrt{-125}\).
Solución
Reescribir\(\ \sqrt{-125}\) en términos de lo radical\(\ i\) y simplificar.
\(\ \sqrt{-125}=i \sqrt{125}=i \sqrt{25 \cdot 5}=5 i \sqrt{5}\)
Simplificar\(\ i^{210}\).
Solución
210÷4=52, con un resto de 2. Por lo tanto,\(\ i^{210}=i^{2}=-1\).
Simplificar\(\ (8-3 i)-(12-i)\).
Solución
Distribuir lo negativo y combinar términos similares.
\(\ (8-3 i)-(12-i)=8-3 i-12+i=-4-2 i\)
Revisar
Simplifica cada expresión y escribe en forma estándar.
- \(\ \sqrt{-9}\)
- \(\ \sqrt{-242}\)
- \(\ 6 \sqrt{-45}\)
- \(\ -12 i \sqrt{98}\)
- \(\ \sqrt{-32} \cdot \sqrt{-27}\)
- \(\ 7 i \sqrt{-126}\)
- \(\ i^{8}\)
- \(\ 16 i^{22}\)
- \(\ -9 i^{65}\)
- \(\ i^{365}\)
- \(\ 2 i^{91}\)
- \(\ \sqrt{-\frac{16}{80}}\)
- \(\ (11-5 i)+(6-7 i)\)
- \(\ (14+2 i)-(20+9 i)\)
- \(\ (8-i)-(3+4 i)+15 i\)
- \(\ -10 i-(1-4 i)\)
- \(\ (0.2+1.5 i)-(-0.6+i)\)
- \(\ 6+(18-i)-(2+12 i)\)
- \(\ -i+(19+22 i)-(8-14 i)\)
- \(\ 18-(4+6 i)+(17-9 i)+24 i\)
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.8.
El vocabulario
| Término | Definición |
|---|---|
| \(\ i\) | \(\ i\)es un número imaginario. \(\ i=\sqrt{-1}\). |
| Valor Absoluto | El valor absoluto de un número es la distancia que el número es de cero. El valor absoluto de un número complejo es la distancia desde el número complejo en el plano complejo hasta el origen. |
| Conjugado complejo | Los conjugados complejos son pares de binomios complejos. El complejo conjugado de\(\ a+bi\) es\(\ a−bi\). Cuando se multiplican los conjugados complejos, el resultado es un solo número real. |
| i | i es un número imaginario. \(\ i=\sqrt{-1}\). |
| Número imaginario | Un número imaginario es un número que se puede escribir como producto de un número real y\(\ i\). |
| parte imaginaria | La parte imaginaria de un número complejo\(\ a+bi\) es\(\ bi\). |
| Números imaginarios puros | Los números imaginarios puros son el subconjunto de números complejos sin partes reales, solamente\(\ bi\). |
| Número Real | Un número real es un número que se puede trazar en una recta numérica. Los números reales incluyen todos los números racionales e irracionales. |
| parte real | La parte real de un número complejo\(\ a+bi\) es\(\ a\). |
| coordenadas rectangulares | Un punto se escribe usando coordenadas rectangulares si se escribe en términos de\(\ x\) y\(\ y\) y se puede graficar en el plano cartesiano. |
| forma rectangular | La forma rectangular de un punto o una curva se da en términos de\(\ x\) y\(\ y\) y se grafica en el plano cartesiano. |
| forma estándar | La forma estándar de un número complejo es\(\ a+bi\) donde a y b son números reales. |
Atribuciones de imagen
- [Figura 1]
Crédito: Por Connelly (charla · contribs) [Dominio público], vía Wikimedia Commons; Squeezyboy
Fuente: https://commons.wikimedia.org/wiki/File%3AMandelset_hires.png; https://www.flickr.com/photos/squeezyboy/3300595223/in/photolist-62EpYc-4pE2wi-57iN5K-6BLGYY-bw4mN7-4pJcEL-4pJ9aq-95hik-4pJ8KL-4pE46e-3SBgZp-4pJ8mQ-4pJfT5-5nsJci-4pE6iB-4pE1ak-pkdG3-8QfWkj-7ty6mZ-5exjuj-4pEbe2-deQ2mt-8YnitG-iYd6yK-9qvRPU-4D8NcE-8dFpKA-83TMea-4xEMyp-daTVZY-taKCLt-biH6oZ-663UrM-bY6Cnw-ffzYYg-7TzAsZ -JBA9HV-8Y2625-7TY6F6-FQSQSV-5oJ6RS-DSJFXM-88R84U-7TC49S-FZFH9a-PGGwCj-7JMUZY-HYU5E5-9C8FRQ-Der5H8
Licencia: CC BY-NC 3.0