4.5.7: Poderes y raíces de números complejos

Poderes y raíces de números complejos

Calcular (simplificar) manualmente una declaración como:\(\ (14-17 i)^{5}\) o\(\ \sqrt[4]{(3-2 i)}\) en forma presente (rectangular) sería un proceso muy intensivo en el mejor de los casos.

Afortunadamente aprenderás en esta lección que existe una alternativa: el teorema de De Moivre. El teorema de De Moivre es realmente el único método práctico para encontrar los poderes o raíces de un número complejo, pero hay una captura...

¿Qué se debe hacer con un número complejo antes de poder utilizar el teorema de De Moivre?

---

Poderes y raíces de números complejos

Poderes de números complejos

¿Cómo elevamos un número complejo a una potencia? Empecemos con un ejemplo:

\(\ (-4-4 i)^{3}=(-4-4 i) \cdot(-4-4 i) \cdot(-4-4 i)\)

En forma rectangular, esto puede llegar a ser muy complejo. ¿Qué pasa en forma r cis θ?

\(\ (-4-4 i)=4 \sqrt{2} \operatorname{cis}\left(\frac{5 \pi}{4}\right)\)

y usando nuestra regla de multiplicación de la sección anterior,

\(\ (-4-4 i)^{3}=(4 \sqrt{2})^{3} \operatorname{cis}\left(\frac{15 \pi}{4}\right)\)

Aviso,\(\ (a+b i)^{3}=r^{3} \text { cis } 3 \theta\)

En palabras: Elevar el valor r hasta el mismo grado en que se eleva el número complejo y luego multiplica eso por cis del ángulo multiplicado por el número del grado.

Reflexionando sobre el ejemplo anterior, podemos identificar el teorema de De Moivre:

Dejar z = r (cos θ + i sin θ) ser un número complejo en forma rcisθ. Si n es un entero positivo, z ⁿ es z ⁿ = r ⁿ (cos (nθ) + i sin (nθ))

Debe quedar claro que la forma polar proporciona un resultado mucho más rápido para elevar un número complejo a una potencia que hacer el problema en forma rectangular.

Raíces de números complejos

Probablemente se dio cuenta hace mucho tiempo que cuando se presenta una nueva operación en matemáticas, a menudo sigue la operación inversa. Eso generalmente se debe a que la operación inversa suele ser procesalmente similar, y tiene sentido aprender ambas al mismo tiempo.

Esto no es una excepción:

La operación inversa de encontrar una potencia para un número es encontrar una raíz del mismo número.

1. Recordemos del álgebra que cualquier raíz puede escribirse como\(\ x^{1 / n}\)
2. Dado que la fórmula para el teorema de De Moivre también funciona para potencias fraccionarias, la misma fórmula puede ser utilizada para encontrar raíces:

   \(\ z^{1 / n}=(a+b i)^{1 / n}=r^{1 / n} \operatorname{cis}\left(\frac{\theta}{n}\right)\)

---

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó qué se le debía hacer a un número complejo antes de poder usar el teorema de De Moivre en él.

Solución

Una operación numérica compleja escrita en forma rectangular, como: (13−4i) ³ debe convertirse a forma polar antes de utilizar el teorema de De Moivre.

Ejemplo 2

Encuentra el valor de\(\ (1+\sqrt{3} i)^{4}\).

Solución

\ (\\ begin {array} {l}
r=\ sqrt {(1) ^ {2} + (\ sqrt {3}) ^ {2}} =2\\
\ tan\ theta_ {r e f} =\ frac {\ sqrt {3}} {1}
\ end {array}\)

y θ está en el primer ^cuadrante, por lo que

\(\ \theta=\frac{\pi}{3}\)

Usando nuestra ecuación de arriba:

\ (\\ begin {array} {l}
z^ {4} =r^ {4}\ text {cis} 4\ theta\\
z^ {4} =( 2) ^ {4} =( 2) ^ {4}\ text {cis} 4\ frac {\ pi} {3}
\ end {array}\)

Expandiendo la forma cis:

\ (\\ begin {array} {l}
z^ {4} =16\ izquierda (\ cos\ izquierda (\ frac {4\ pi} {3}\ derecha) +i\ sin\ izquierda (\ frac {4\ pi} {3}\ derecha)\ derecha)\
=16 ((-0.5) -0.866 i)
\ end {array}\)

Finalmente tenemos

\(\ z^{4}=-8-13.856 i\)

Ejemplo 3

Encontrar\(\ \sqrt{1+i}\).

Solución

Primero, reescribir en forma exponencial:\(\ (1+i)^{1 / 2}\)

Y ahora en forma polar:

\(\ \sqrt{1+i}=\left(\sqrt{2} \operatorname{cis}\left(\frac{\pi}{4}\right)\right)^{1 / 2}\)

Expandiendo la forma cis,

\(\ =\left(\sqrt{2}\left(\cos \left(\frac{\pi}{4}\right)+i \sin \left(\frac{\pi}{4}\right)\right)\right)^{1 / 2}\)

Usando la fórmula:

\ (\\ begin {array} {l}
=\ izquierda (2^ {1/2}\ derecha) ^ {1/2}\ izquierda (\ cos\ izquierda (\ frac {1} {2}\ cdot\ frac {\ pi} {4}\ derecha) +i\ sin\ izquierda (\ frac {1} {2}\ cdot\ frac {\ pi} {4}\ derecha)\ derecha)\\
=2^ {1/4}\ izquierda (\ cos\ izquierda (\ frac {\ pi} {8}\ derecha) +i\ sin\ izquierda (\ frac {\ pi} {8}\ derecha)\ derecha)
\ end {array }\)

En forma decimal, obtenemos

\ (\\ begin {array} {l}
=1.189 (0.924+0.383 i)\\
=1.099+0.455 i
\ end {array}\)

Para verificar, multiplicaremos el resultado por sí mismo en forma rectangular:

\ (\\ begin {array} {l}
(1.099+0.455 i)\ cdot (1.099+0.455 i) =1.099^ {2} +1.099 (0.455 i) +1.099 (0.455 i) + (0.455 i) ^ {2}\\
=1.208+0.500 i+0.500 i+0.208 i^ {2}\\
=1.208+i-0.208\ text {o}\\
=1+i
\ end {array}\)

Ejemplo 4

Encuentra el valor de\(\ x: x^{3}=(1-\sqrt{3} i)\)

Solución

Primero ponemos\(\ 1-\sqrt{3} i\) en forma polar.

Utilizar\(\ x=1, y=-\sqrt{3}\) para obtener\(\ r=2, \theta=\frac{5 \pi}{3}\)

dejar\(\ z=(1-\sqrt{3} i)\) en forma rectangular

\(\ z=2 \operatorname{cis}\left(\frac{5 \pi}{3}\right)\)en forma polar

\(\ x=(1-\sqrt{3} i)^{1 / 3}\)

\(\ x=\left[2 \operatorname{cis}\left(\frac{5 \pi}{3}\right)\right]^{1 / 3}\)

Usa el teorema de De Moivre para encontrar la primera solución:

\(\ x_{1}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi / 3}{3}\right) \text { or } 2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}\right)\)

Deja la respuesta en forma cis para encontrar las soluciones restantes:

n = 3 lo que significa que las 3 soluciones están separadas por\(\ \frac{2 \pi}{3}\) radianes o

\(\ x_{2}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}+\frac{2 \pi}{3}\right)\)y\(\ x_{3}=2^{1 / 3} \operatorname{cis}\left(\frac{5 \pi}{9}+\frac{2 \pi}{3}+\frac{2 \pi}{3}\right)\)

Nota

No es necesario\(\ \frac{2 \pi}{3}\) volver a agregar. Sumando\(\ \frac{2 \pi}{3}\) tres veces iguales\(\ 2 \pi\). Eso resultaría en rotar alrededor de un círculo completo y comenzar por donde todo comenzó- esa es la primera solución.

Las tres soluciones son:

\ (\\ begin {array} {l}
x_ {1} =2^ {1/3}\ nombreoperador {cis}\ izquierda (\ frac {5\ pi} {9}\ derecha)\
x_ {2} =2^ {1/3}\ nombreoperador {cis}\ izquierda (\ frac {11\ pi} {9}\ derecha)\
x_ {3} =2^ {1/3}\ nombreoperador {cis}\ izquierda (\ frac {17\ pi} {9}\ derecha)
\ end {array}\)

Cada una de estas soluciones, cuando se grafica será\(\ \frac{2 \pi}{3}\) aparte.

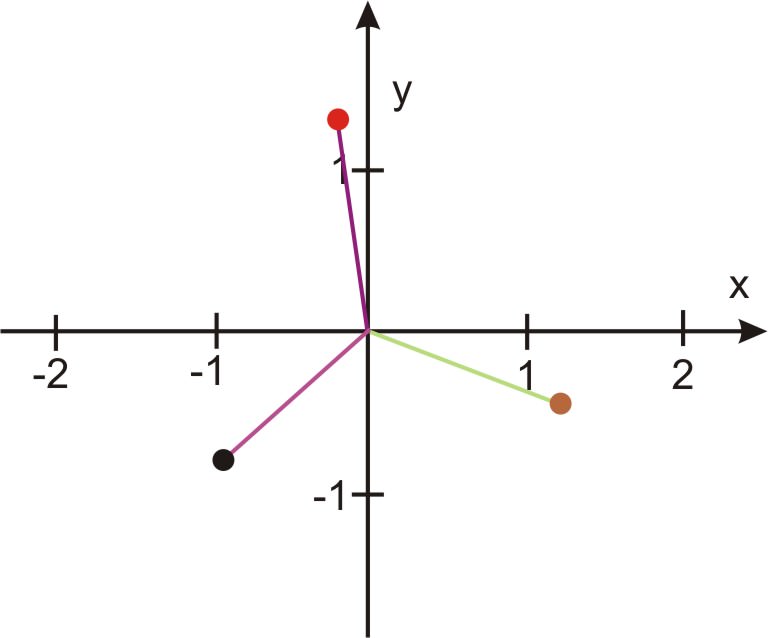
Consulta cualquiera de estas soluciones para ver si los resultados están confirmados.

Comprobando la segunda solución:

\ (\\ begin {array} {l}
x_ {2} =2^ {1/3}\ nombreoperador {cis}\ izquierda (\ frac {11\ pi} {9}\ derecha)\
= 1.260\ izquierda [\ cos\ izquierda (\ frac {11\ pi} {9}\ derecha) +i\ sin\ izquierda (\ frac {11\ pi} {9}\ derecha)\ derecha]\\
=1.260 [-0.766-0.643 i]\\
=-0.965-0.810 i\\
\ text {Hace } (-0.965-0.810 i) ^ {3}\ text {o} (-0.965-0.810 i) (-0.965-0.810 i) (-0.965-0.810 i)\\
=( 1-\ sqrt {3} i)?
\ end {array}\)

Ejemplo 5

¿Cuáles son las dos raíces cuadradas de i?

Solución

Vamos\(\ z=\sqrt{0+i}\).

\(\ r=1, \theta=\pi / 2 \text { or } z=\left[1 \times \operatorname{cis} \frac{\pi}{2}\right]^{1 / 2}\)Utilizando el teorema de De Moivre:

\(\ z_{1}=\left[1 \times \operatorname{cis} \frac{\pi}{4}\right] \text { or } z_{2}=\left[1 \times \operatorname{cis} \frac{5 \pi}{4}\right]\)

\(\ z_{1}=1\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right) \text { or } z_{2}=1\left(\cos \frac{5 \pi}{4}+i \sin \frac{5 \pi}{4}\right)\)

\(\ z_{1}=0.707+0.707 i \text { or } z_{2}=-0.707-0.707 i\)

Verifique la solución z ₁:\(\ (0.707+0.707 i)^{2}=i ?\)

\(\ 0.500+0.500 i+0.500 i+0.500 i^{2}=0.500+i+0.500(-1) \text { or } i\)

Ejemplo 6

Calcular\(\ \sqrt[4]{(1+0 i)}\). ¿Cuáles son las cuatro cuartas raíces de 1?

Solución

Vamos\(\ z=1 \text { or } z=1+0 i\). Entonces el problema se convierte en hallazgo\(\ z^{1 / 4}=(1+0 i)^{1 / 4}\).

Desde\(\ r=1 \theta=0, z^{1 / 4}=[1 \times \operatorname{cis} 0]^{1 / 4}\) con\(\ z_{1}=1^{1 / 4}\left(\cos \frac{0}{4}+i \sin \frac{0}{4}\right)\) o\(\ 1(1+0)\) o\(\ 1\)

Esa raíz no es una sorpresa. Ahora usa De Moivre para encontrar las otras raíces:

\(\ z_{2}=1^{1 / 4}\left[\cos \left(0+\frac{\pi}{2}\right)+i \sin \left(0+\frac{\pi}{2}\right)\right]\)Ya que hay 4 raíces, dividiendo\(\ 2 \pi\) por 4 rendimientos\(\ 0.5 \pi\)\(\ 0+i\) o simplemente\(\ i\)\(\ z_{3}=1^{1 / 4}\left[\cos \left(0+\frac{2 \pi}{2}\right)+i \sin \left(0+\frac{2 \pi}{2}\right)\right]\) cuales rendimientos\(\ z_{3}=-1\)

Por último,\(\ z_{4}=1^{1 / 4}\left[\cos \left(0+\frac{3 \pi}{2}\right)+i \sin \left(0+\frac{3 \pi}{2}\right)\right]\) o\(\ z_{4}=-i\)

Las cuatro cuartas raíces de 1 son 1, i, -1 y -i.

Ejemplo 7

Calcular\(\ (\sqrt{3}+i)^{7}\).

Solución

Para calcular\(\ (\sqrt{3}+i)^{7}\) inicio convirtiendo a forma rcis.

Primero, encuentra r. Recordar\(\ r=\sqrt{\sqrt{3}^{2}+1^{2}}\).

\ (\\ begin {array} {l}
r=\ sqrt {3+1}\\
r=2
\ end {array}\)

Si\(\ \cos \theta=\frac{\sqrt{3}}{2}\) y\(\ \sin \theta=\frac{1}{2}\) entonces\(\ \theta=30^{\circ}\) y está en cuadrante I. Ahora que tenemos forma trigonométrica, el resto es fácil:

\(\ (\sqrt{3}+i)^{7}=\left[2\left(\cos 30^{\circ}+i \sin 30^{\circ}\right)\right]^{7}\)... Escribe el problema original en forma rcis

\(\ 2^{7}\left[\left(\cos \left(7 \cdot 30^{\circ}\right)+i \sin \left(7 \cdot 30^{\circ}\right)\right]\right.\)... Teorema de De Moivre

\(\ 128\left[-\frac{\sqrt{3}}{2}+\frac{-1}{2} i\right]\)... Simplificar

\(\ (\sqrt{3}+i)^{7}=-64 \sqrt{3}-64 i\)... Simplificar de nuevo

\(\ \therefore(\sqrt{3}+i)^{7}=-64 \sqrt{3}-64 i\)

---

Revisar

Realice la operación indicada en estos números complejos:

1. Dividir:\(\ \frac{2+3 i}{1-i}\)
2. Multiplicar:\(\ (-6-i)(-6+i)\)
3. Multiplicar:\(\ \left(\frac{\sqrt{3}}{2}-\frac{1}{2} i\right)^{2}\)
4. Encuentra el producto usando forma polar:\(\ (2+2 i)(\sqrt{3}-i)\)
5. Multiplicar:\(\ 2\left(\cos 40^{\circ}+i \sin 40^{\circ}\right) \cdot 4\left(\cos 20^{\circ}+i \sin 20^{\circ}\right)\)
6. Multiplicar:\(\ 2\left(\cos \frac{\pi}{8}+i \sin \frac{\pi}{8}\right) \cdot 2\left(\cos \frac{\pi}{10}+i \sin \frac{\pi}{10}\right)\)
7. Dividir:\(\ 2\left(\cos 80^{\circ}+i \sin 80^{\circ}\right) \div 6\left(\cos 200^{\circ}+i \sin 200^{\circ}\right)\)
8. Dividir:\(\ 3 \operatorname{cis}\left(130^{\circ}\right) \div 4 \operatorname{cis}\left(270^{\circ}\right)\)

Usa el teorema de De Moivre.

9. \(\ \left[3\left(\cos 80^{\circ}+i \sin 80^{\circ}\right)\right]^{3}\)
10. \(\ \left[\sqrt{2}\left(\cos \frac{5 \pi}{16}+i \sin \frac{5 \pi}{16}\right)\right]^{4}\)
11. \(\ (\sqrt{3}-i)^{6}\)
12. Identificar las 3 raíces cubitas complejas de\(\ 1+i\)
13. Identificar las 4 cuartas raíces complejas de\(\ -16 i\)
14. Identificar las cinco quintas raíces complejas de\(\ i\)

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.10.

---

El vocabulario

Término	Definición
número complejo	Un número complejo es la suma de un número real y un número imaginario, escritos en la forma a+bi.
Teorema de De Moivre	El teorema de De Moivre es el único método manual práctico para identificar los poderes o raíces de los números complejos. El teorema establece que si z=r (cosθ+isinθ) es un número complejo en forma rcisθ y n es un entero positivo, entonces z ^n = r ^n (cos (nθ) +isin (nθ)).