5.4.1: Ecuación vectorial de una línea
- Page ID
- 108943
Ecuación vectorial de una línea
El control de tránsito aéreo está rastreando dos aviones en las inmediaciones de su aeropuerto. En un momento dado, un avión se encuentra en una ubicación 45 km al este y 120 km al norte del aeropuerto a una altitud de 7.5 km. El segundo avión se encuentra a 63 km al este y 96 km al sur del aeropuerto a una altitud de 6.0 km. El primer avión está volando directamente hacia el aeropuerto mientras que el segundo avión continúa a una altitud constante con un rumbo definido por el vector\(\ \overrightarrow{h_{2}}=\langle 3,4,0\rangle\) para aterrizar eventualmente en otro aeropuerto al noroeste de nuestros controladores aéreos. ¿Se cruzan los caminos de estos dos aviones?
Ecuación vectorial de una línea
Probablemente estés muy familiarizado con el uso de y = mx + b, la forma pendiente-intercepción, como la ecuación de una línea. Si bien esta ecuación funciona bien en el espacio bidimensional, es insuficiente para definir completamente la ecuación de una línea en espacios de orden superior.
Líneas en el espacio
En un plano bidimensional, una línea puede ser representada por la ecuación y = mx + b, donde m es la pendiente de la línea y b es la intersección y. En el espacio tridimensional, esta ecuación puede representar una línea o un plano o la proyección de una línea 3D sobre el plano x-y. Por ejemplo, en el diagrama de abajo, la línea de la izquierda pasa por los puntos P y Q. La ecuación en el espacio 2D para esta línea es\(\ y=\frac{-P}{Q} x+P\)
Las tres líneas anaranjadas en el diagrama a la derecha de abajo también pueden ser descritas por esta ecuación. Los tres tienen pendiente\(\ M=\frac{-P}{Q}\) e intercepción en Y B = P. Si queremos especificar una de estas líneas en particular, necesitamos identificar la línea como la intersección de dos planos. Por ejemplo, la línea donde\(\ y=\frac{-P}{Q} x+P\) y\(\ z=0\) para todos los puntos es la intersección de los planos naranja y verde en el diagrama de abajo a la derecha. (Recuerde que los planos naranja y verde se dibujan con bordes por conveniencia, pero que representan planos que se extienden hacia el infinito hacia afuera).
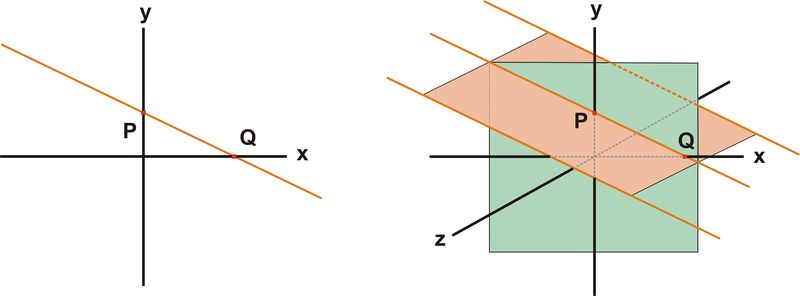
Por lo tanto, podemos especificar una línea particular requiriendo que las ecuaciones para ambos planos sean simultáneamente verdaderas. En una sección anterior desarrollamos una ecuación para un plano dado por d = - n x x o - n y y o - n z z o. En este caso Qy + Px - QP = 0 y z = 0 deben satisfacerse ambos para todos los puntos de la línea que pasan por los puntos P y Q.
Encontrar la ecuación vectorial de una línea
Otra forma de identificar puntos en una línea se puede encontrar usando el método de adición de vectores que discutimos anteriormente en este capítulo. Para encontrar el vector de posición\(\ \vec{r}\), para cualquier punto a lo largo de una línea, podemos agregar el vector de posición de un punto en la línea que ya conocemos y agregar a eso un vector,\(\ \vec{v}\), que se encuentra en la línea como se muestra en el diagrama de abajo.
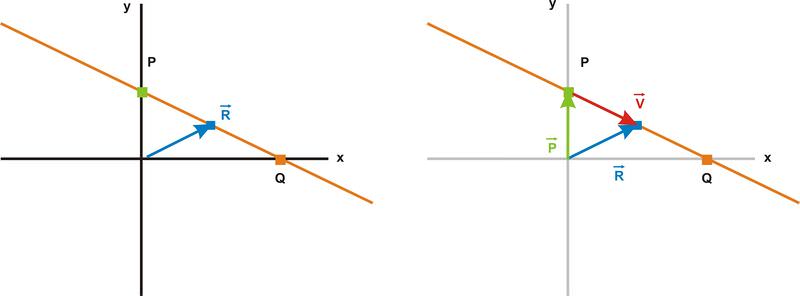
El vector de posición\(\ \vec{R}\) para un punto entre P y Q viene dado por\(\ \vec{R}=\vec{p}+\vec{v}\)
Todos los demás puntos de esta línea se pueden alcanzar viajando a lo largo de la línea desde el punto P, por lo tanto, el vector de posición para cualquier punto de la línea viene dado por\(\ \vec{r}=\vec{p}+k \vec{v}\).
Si conocemos las ubicaciones de dos puntos en una línea, podemos determinar la ecuación de la línea. Todos los puntos de una línea cumplen la ecuación\(\ \vec{r}=\vec{p}+k \vec{v}\), donde k es un escalar que varía de -∞ a ∞. Si ya conocemos los vectores de posición para dos puntos en la línea\(\ \vec{q}\),\(\ \vec{p}\) y, podemos utilizar el método de resta vectorial para determinar la ecuación del vector,\(\ \vec{v}=\vec{p}-\vec{q}\). Por lo tanto\(\ \vec{r}=\vec{p}+k(\vec{p}-\vec{q})\),, donde k varía de -∞ a ∞.
Ecuaciones vectoriales generales
En general, una ecuación vectorial es cualquier función que toma una o más variables y devuelve un vector. La ecuación vectorial de una línea es una ecuación que identifica el vector de posición de cada punto a lo largo de la línea. Esto funciona para líneas rectas y para curvas. Por ejemplo, la ecuación vectorial\(\ \vec{p}=\langle 3 \cos \theta, 3 \sin \theta, 2\rangle\) define un círculo que tiene un radio de 3 unidades que se asienta paralelo al plano x-y a una distancia de 2 unidades a lo largo del eje z como se muestra a continuación. La línea naranja es el conjunto de puntos que satisfacen la ecuación vectorial,\(\ \vec{p}=\langle 3 \cos \theta, 3 \sin \theta, 2\rangle\) mientras que las líneas grises son varios vectores de posición individuales que satisfacen la ecuación vectorial.
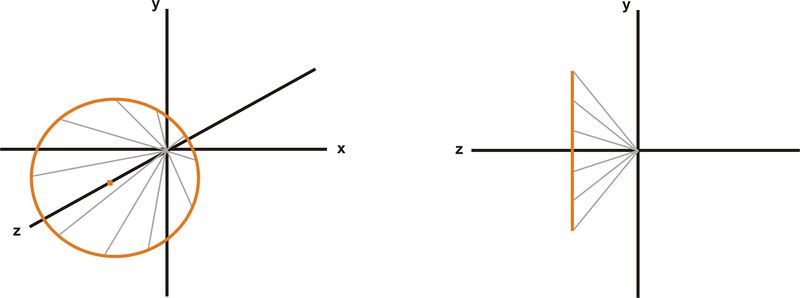
Ejemplos
Antes, se le hizo una pregunta sobre dos aviones.
El control de tránsito aéreo está rastreando dos aviones en las inmediaciones de su aeropuerto. En un momento dado, un avión se encuentra en una ubicación 45 km al este y 120 km al norte del aeropuerto a una altitud de 7.5 km. El segundo avión se encuentra a 63 km al este y 96 km al sur del aeropuerto a una altitud de 6.0 km. El primer avión está volando directamente hacia el aeropuerto mientras que el segundo avión continúa a una altitud constante con un rumbo definido por el vector\(\ \overrightarrow{h_{2}}=\langle 3,4,0\rangle\) para aterrizar eventualmente en otro aeropuerto al noroeste de nuestros controladores aéreos. ¿Se cruzan los caminos de estos dos aviones?
Solución
Lo primero que tenemos que hacer es determinar los vectores de posición de los dos planos. Definir nuestro aeropuerto como el origen de las coordenadas y definir\(\ \hat{x}=\text { east }\),\(\ \hat{y}=\text { north }\), y\(\ \hat{z}=\text { upward }\). Llamar a la posición del avión #1, P, y la posición del plano #2, Q. Esto da\(\ \vec{p}=\langle 45,120,7.5\rangle\) y\(\ \vec{q}=\langle 63,-96,6.0\rangle\).
El avión #1 se dirige directamente hacia el aeropuerto. El vector desde la posición del plano #1 hasta el origen viene dado por
\ (\\ begin {array} {l}
\ vec {v} =\ vec {o} -\ vec {p} =\ langle (0-45), (0-120), (0-7.5)\ rangle\
\ vec {v} =\ vec {p} -\ vec {q} =\ langle-45, -120, -7.5\ rangle
\ end {array}\)
La ecuación de la línea que representa el movimiento del plano #1 se convierte entonces
\(\ \overrightarrow{r_{1}}=\langle 45,120,7.5\rangle+k_{1}\langle-45,-120,-7.5\rangle \quad \overrightarrow{r_{1}}=\langle 45,120,7.5\rangle+k_{1}\langle-45,-120,-7.5\rangle\)
El avión #2 continúa a una altitud constante con rumbo\(\ \overrightarrow{h_{2}}=\langle 3,4,0\rangle\). La ecuación de la línea que representa el movimiento del plano #2 se convierte entonces
\ (\\ begin {array} {l}
\ vec {r} _ {2} =\ langle-63,96,6.0\ rangle+k_ {2}\ langle 3,4,0\ rangle\ quad\ overrightarrow {r_ {2}} =\ langle 63, -96,6.0\ rangle+k_ {2}\ langle 3,4,0\ rangle\
\ overrightarrow tarrow {r_ {2}} =\ langle-63,96,6.0\ alcance+k_ {2}\ langle 3,4,0\ rangle\
\ overrightarrow {r_ {1}} =\ langle 45,120,7.5\ rangle+k_ {1}\ langle-45, -120, -7.5\ rangle
\ end {array}\)
Si los caminos de los dos planos se cruzan, la posición de esa intersección debe tener coordenadas que satisfagan ambas ecuaciones.
Para satisfacer ambas ecuaciones, r 1 x debe ser igual a r 2 x, r 1 y debe ser igual a r 2 y, y r 1 z debe ser igual a r 2 z. Esto significa que 45 - 45 k 1 = 63 + 3 k 2, 120 - 120 k 1 = -96 + 4 k 2, y 7.5 - 7.5 k 1 = 6.0 + 0 k 2 todos deben ser simultáneamente verdaderos.
La primera ecuación simplifica a 15 - 15 k 1 = 21 + k 2 o k 2 = -6 - 15 k 1. El segundo simplifica a 30 - 30 k 1 = -24 + k 2 o k 2 = 54 - 30 k 1. La tercera ecuación simplifica a 7.5 - 7.5 k 1 = 6 o\(\ k_{1}=\frac{1}{5}\).
Insertando el valor de k 1 de la tercera ecuación en las dos primeras ecuaciones, encontramos\(\ k_{2}=-6-15\left(\frac{1}{5}\right)=-6-3=-9 \text { and } k_{2}=54-30 k_{1}=54-30\left(\frac{1}{5}\right)=54-6=48\)
Dado que k 2 = 33 y k 2 = 0 no pueden ser simultáneamente verdaderos, los caminos de los dos planos no se cruzan.
Nota: Hay otras formas de razonar a través de este problema. ¿Puedes encontrar alguna? (Pista: Piense en la geometría en 2 dimensiones, o concéntrese en la altitud como una forma de simplificar este problema).
Escribe la ecuación de\(\ y=-\frac{5}{3} x+5\) como una ecuación vectorial.
Solución
Comienza eligiendo dos puntos en la línea, digamos\(\ (3,0)\) y\(\ (6,-5)\). Entonces\(\ \vec{p}=\langle 3,0\rangle\) y\(\ \vec{q}=\langle 6,-5\rangle\) Entonces,
\(\ \vec{p}-\vec{q}=\langle 3,0\rangle-\langle 6,-5\rangle=\langle 3-6,0-(-5)\rangle=\langle-3,5\rangle\)
Finalmente, la ecuación vectorial de la línea es
\(\ \vec{r}=\langle 3,0\rangle+k\langle-3,5\rangle=\langle 3-3 k, 5 k\rangle\)
Escribe la ecuación vectorial de la línea definida por los puntos (2, 3, 4) y (-5, 2, -1).
Solución
Estos dos puntos tienen vectores de posición. El vector de la línea que conecta los dos puntos viene dado por
\ (\\ begin {array} {l}
\ vec {v} =\ vec {p} -\ vec {q} =\ langle (2- (-5)), (3-2), (4- (-1))\ rangle\
\ hat {v} =\ vec {p} -\ vec {q} =\ langle 7,1,5\ rangle
\ end {array}\)
La ecuación de la línea se convierte entonces
\(\ \vec{r}=\langle 2,3,4\rangle+k\langle 7,1,5\rangle \quad \vec{r}=\langle 2,3,4\rangle+k\langle 7,1,5\rangle\)
Determinar la ecuación para la línea definida por los puntos P = (6, 7, 5) y Q = (3, 2, 11). Después encuentra el vector de posición para un punto, R, a medio camino entre estos dos puntos.
Solución
\ (\\ begin {array} {l}
\ vec {v} =\ vec {p} -\ vec {q} =\ langle (6-3), (7-2), (5-11)\ rangle\
\ hat {v} =\ vec {p} -\ vec {q} =\ langle 3,5, -6\ rangle
\ end {array}\)
La ecuación de la línea se convierte entonces
\(\ \vec{r}=\langle 6,7,5\rangle+k\langle 3,5,-6\rangle \quad \vec{r}=\langle 6,7,5\rangle+k\langle 3,5,-6\rangle\)
Dado que el vector\(\ \vec{v}\) apunta desde P, el valor de k para un punto en particular nos da alguna información sobre la ubicación de ese punto. Si 0 < k < 1, el punto se encuentra en la línea entre P y Q. Si k < 0, el punto no está entre P y Q y está más cerca de P que Q. Si k > 1, el punto se encuentra en la línea entre P y Q. Si k < 0, el punto no está entre P y Q y está más cerca de P que Q. El punto a mitad de camino entre los dos puntos tiene\(\ k=\frac{1}{2}\).
\ (\\ begin {array} {l}
\ vec {R} =\ langle 6,7,5\ rangle+\ frac {1} {2}\ langle 3,5, -6\ rangle\
\ vec {R} =\ langle (6+1.5), (7+2.5), (5+ (-3)\ rangle=\ langle 7.5,9.5,2\ rangle
\ end {array}\)
¿Los dos vectores\(\ \vec{D}=\langle 1,-1,4\rangle+d\langle 1,-1,1\rangle\) y las líneas\(\ \vec{F}=\langle 2,4,7\rangle+f\langle 2,1,3\rangle\) sesgadas o se cruzan entre sí?
Solución
Si los dos vectores se cruzan, debe haber un punto identificado por el vector de posición\(\ \vec{p}\) que satisfaga las ecuaciones de ambas líneas. Es decir, debemos ser capaces de encontrar valores para d y f tales que\(\ \vec{D}=\vec{F}\) o\(\ \langle 1,-1,4\rangle+d\langle 1,-1,1\rangle=\langle 2,4,7\rangle+f\langle 2,1,3\rangle\).
Cada uno de los tres componentes de vectores\(\ \vec{D}\) y\(\ \vec{F}\) debe ser independientemente igual si\(\ \vec{D}=\vec{F}\). Esto significa que 1 + d = 2 + 2 f, -1 - d = 4 + f, y 4 + d = 7 + 3 f Combinando las dos primeras ecuaciones da: 1 + d - 1 - d = 2 + 2 f + 4 + f que cuando se simplifica se convierte en 0 = 6 + 3 f o f = -2. Si sustituimos esto de nuevo en la primera ecuación que obtenemos, 1 + d = 2 + 2 (-2) que al simplificarse se convierte en d = -3. Si las dos líneas se cruzan, f = -2 y d = -3 deben satisfacer cada una de las ecuaciones de componentes.
1 + d = 2 + 2 f se convierte en 1 + (-3) = 2 + 2 (-2) o -2 = -2
-1 - d = 4 + f se convierte en -1 - (-3) = 4 + (-2) o +2 = +2
4 + d = 7 + 3 f se convierte en 4 + (-3) = 7 + 3 (-2) o +1 = +1
Las tres ecuaciones están igualmente satisfechas, por lo que las dos líneas sí se cruzan y el punto de intersección es (-2, 2, 1).
En física, el movimiento de un objeto que viaja a una velocidad constante es descrito por la ecuación\(\ \overrightarrow{s_{t}}=\overrightarrow{s_{i}}+\vec{v} t\) donde s i es la posición inicial, s es la posición en algún momento posterior t, y v es la velocidad del objeto. Escribe la ecuación vectorial que devuelve el conjunto de vectores de posición\(\ \vec{s}\) para un objeto que tiene una posición inicial\(\ \overrightarrow{s_{i}}=\langle 2,3,4\rangle\) y una velocidad de\(\ \vec{v}=\langle 1,1,-2\rangle\) y determina la ubicación del objeto en t = 10s.
Solución
\ (\\ begin {array} {l}
\ overrightarrow {s_ {t}} =\ overrightarrow {s_ {i}} +\ vec {v} t=\ langle 2,3,4\ rangle+t\ langle 1,1, -2\ rangle=\ langle 2+t, 3+t, 4-2 t\ rangle\\ texto {At} t=10 s,
\ overrightarrow {s_ {t}} = rightarrow {s_ {10}} =\ langle 2+10,3+10,4-2 (10)\ rangle=\ langle 12,13, -16\ rangle
\ end {array} \)
Un objeto tiene una posición de\(\ \overrightarrow{s_{i}}=\langle 3,3,6\rangle\) a t = 0 y una velocidad de\(\ \vec{v}=\langle 10,7,3\rangle\). Utilice la ecuación vectorial\(\ \vec{s}=\overrightarrow{s_{i}}+\vec{v} t\) para determinar la distancia recorrida por el objeto entre t = 3s y t = 5s. Distancia medida en metros.
Solución
La ecuación vectorial que describe el movimiento del objeto es
\(\ \vec{s}=\vec{s}_{i}+\vec{v} t=\langle 3,3,6\rangle+t\langle 10,7,3\rangle=\langle 3+10 t, 3+7 t, 6+3 t\rangle\)
La posición del objeto en t = 3s se obtiene de la ecuación vectorial:
\(\ \overrightarrow{s_{3}}=\overrightarrow{s_{i}}+\vec{v} t=\langle 3,3,6\rangle+(3)\langle 10,7,3\rangle=\langle 3+10(3), 3+7(3), 6+3(3)\rangle=\langle 33,24,15\rangle\)
La posición del objeto en t = 5s se obtiene de la ecuación vectorial:
\(\ \overrightarrow{s_{5}}=\overrightarrow{s_{i}}+\vec{v} t=\langle 3,3,6\rangle+(5)\langle 10,7,3\rangle=\langle 3+10(5), 3+7(5), 6+3(5)\rangle=\langle 53,38,21\rangle\)
La distancia recorrida entre estos dos puntos es la magnitud del vector comenzando en (33, 24, 15) y terminando en (53, 38, 21).
\(\ \overrightarrow{\triangle s}=\overrightarrow{s_{5}}-\overrightarrow{s_{3}}=\langle 53,38,21\rangle-\langle 33,24,15\rangle=\langle 20,14,6\rangle\)
Ahora podemos usar el teorema de Pitágoras para determinar la magnitud del vector.
\(\ \overrightarrow{|\triangle s|}=\sqrt{a^{2}+b^{2}+c^{2}}=\sqrt{(20)^{2}+(14)^{2}+(6)^{2}}=25.1 \text { meters }\)
Determinar la ecuación vectorial de la línea recta definida por los puntos (2, 2, 2) y (1, 3, 5).
Solución
Estos dos puntos tienen vectores de posición\(\ \vec{p}=\langle 2,2,2\rangle\) y\(\ \vec{q}=\langle 1,3,5\rangle\). El vector de la línea que conecta los dos puntos viene dado por
\(\ \vec{v}=\vec{p}-\vec{q}=\langle(2-1),(2-3),(2-5)\rangle=\langle 1,-1,-3\rangle\)
La ecuación de la línea,\(\ \vec{r}=\vec{p}+k \vec{v}\), luego se convierte
\(\ \vec{r}=\langle 2,2,2\rangle+k\langle 1,-1,-3\rangle \quad \vec{r}=\langle 2,2,2\rangle+k\langle 1,-1,-3\rangle\)
¿Las dos líneas\(\ \vec{R}=\langle 4,4,-2\rangle+r\langle-3,7,2\rangle\) y se\(\ \vec{K}=\langle 9,-8,7\rangle+k\langle-2,1,3\rangle\) cruzan?
Solución
Si los dos vectores se cruzan, debe haber un punto identificado por el vector de posición\(\ \vec{p}\) que satisfaga las ecuaciones de ambas líneas. En otras palabras, debemos ser capaces de encontrar valores para r y k de tal manera que
\(\ \vec{R}=\vec{K}\)o\(\ \langle 4,4,-2\rangle+r\langle-3,7,2\rangle=\langle 9,-8,7\rangle+k\langle-2,1,3\rangle\).
Cada uno de los tres componentes de vectores\(\ \vec{R}\) y\(\ \vec{K}\) debe ser independientemente igual si\(\ \vec{R}=\vec{K}\). Esto significa que 4 - 3 r = 9 - 2 k, 4 + 7 r = -8 + k, y -2 + 2 r = 7 + 3 k
Resolver la segunda ecuación para k da 12 + 7 r = k. Ahora sustituya esto en una de las otras dos ecuaciones: 4 - 3 r = 9 - 2 (12 + 7 r) o 4 - 3 r = 9 - 24 - 14 r lo que simplifica a 19 = -11 r o\(\ r=\frac{-19}{11}=-1.727\). Sustituir este valor por una de las otras ecuaciones: -2 + 2 (-1.727) = 7 + 3 k que se convierte en -2 - 3.454 = 7 + 3 k. Resolviendo para k da k = -4.151. Si las dos líneas se cruzan, r = -1.727 y k = -4.151 deben satisfacer cada una de las ecuaciones componentes.
4 - 3 r = 9 - 2 k se convierte en 4 - 3 (-1.727) = 9 - 2 (-4.151) o -1.181 = 17.302 Dado que incluso esta primera ecuación no se mantiene cierta, estas dos líneas están sesgadas y no se cruzan.
Revisar
Escribe la ecuación vectorial de la línea definida por los siguientes puntos:
- (2, −2,5) y (1,5,4)
- (2, −9,5) y (8,4, −6)
- (15,3, −3) y (4, −3,9)
- (−1, −1,7) y (3,11,8)
- (1, −3,2) y (−5,3, −1)
- (25,17,42) y (−16,12,23)
Determina si los dos vectores son líneas sesgadas o si se cruzan entre sí.
- \(\ \vec{D}=\langle 2,3,1\rangle+d\langle 5,3,6\rangle\)y\(\ \vec{F}=\langle-5,-3,-5\rangle+f\langle 15,3,-3\rangle\)
- \(\ \vec{D}=\langle 3,4,7\rangle+d\langle 3,3,2\rangle\)y\(\ \vec{F}=\langle-2,11,7\rangle+f\langle-2,11,7\rangle\)
- \(\ \vec{D}=\langle 15,3,-3\rangle+d\langle 3,11,8\rangle\)y\(\ \vec{F}=\langle 5,3,6\rangle+f\langle 1,-4,6\rangle\)
- \(\ \vec{D}=\langle 13,-1,6\rangle+d\langle-5,4,12\rangle\)y\(\ \vec{F}=\langle 6,9,0\rangle+f\langle 21,0,14\rangle\)
Identifica el vector de posición para el punto medio de cada línea (ya encontraste las ecuaciones vectoriales en los problemas 1 a 4).
- (2, −2,5) y (1,5,4)
- (2, −9,5) y (8,4, −6)
- (15,3, −3) y (4, −3,9)
- (−1, −1,7) y (3,11,8)
Utilice la ecuación vectorial, y los siguientes valores para t: t = 3s y t = 5s. Distancia medida en metros.
- Un objeto tiene una posición de\(\ \overrightarrow{s_{i}}=\langle 3,-5,1\rangle\) a t = 0 y una velocidad de\(\ \vec{v}=\langle 2,7,-3\rangle\)
- Un objeto tiene una posición de\(\ \overrightarrow{s_{i}}=\langle 1,-4,-8\rangle\) a t = 0 y una velocidad de\(\ \vec{v}=\langle 9,-7,3\rangle\)
- Un objeto tiene una posición de\(\ \overrightarrow{s_{i}}=\langle-1,2,-3\rangle\) a t = 0 y una velocidad de\(\ \vec{v}=\langle 3,-1,-2\rangle\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.10.
El vocabulario
| Término | Definición |
|---|---|
| vector de posición | Un vector de posición describe el recorrido en línea recta entre un punto de partida (generalmente el origen) y la ubicación de un segundo punto en un plano de coordenadas. |
| Líneas sesgadas | Las líneas sesgadas son líneas que están en diferentes planos y nunca se cruzan. |
| ecuación vectorial | Una ecuación vectorial es cualquier función que toma una o más variables y devuelve un vector. |

