6.4.1: Círculos Centrados en el Origen

Última actualización
Guardar como PDF

Page ID: 108892

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Círculos Centrados en el Origen

Se dibuja un círculo que está centrado en el origen. Se mide el diámetro del círculo para ser 32 unidades. ¿El punto\(\ (14,8)\) se encuentra en el círculo?

Círculos Centrados en el Origen

Hasta ahora, su única referencia a los círculos era desde la geometría. Un círculo es el conjunto de puntos que son equidistantes (el radio) de un punto dado (el centro). Un segmento de línea que pasa por el centro y tiene puntos finales en el círculo es un diámetro.

Ahora, tomaremos un círculo y lo colocaremos en el plano x−y para ver si podemos encontrar su ecuación. En este concepto, vamos a colocar el centro del círculo sobre el origen.

Encontrar la ecuación de un círculo

Paso 1: En una hoja de papel cuadriculado, dibuja un plano x−y. Usando una brújula, dibuja un círculo, centrado en el origen que tiene un radio de 5. Encuentra el punto (3,4) en el círculo y dibuja un triángulo rectángulo con el radio como la hipotenusa.

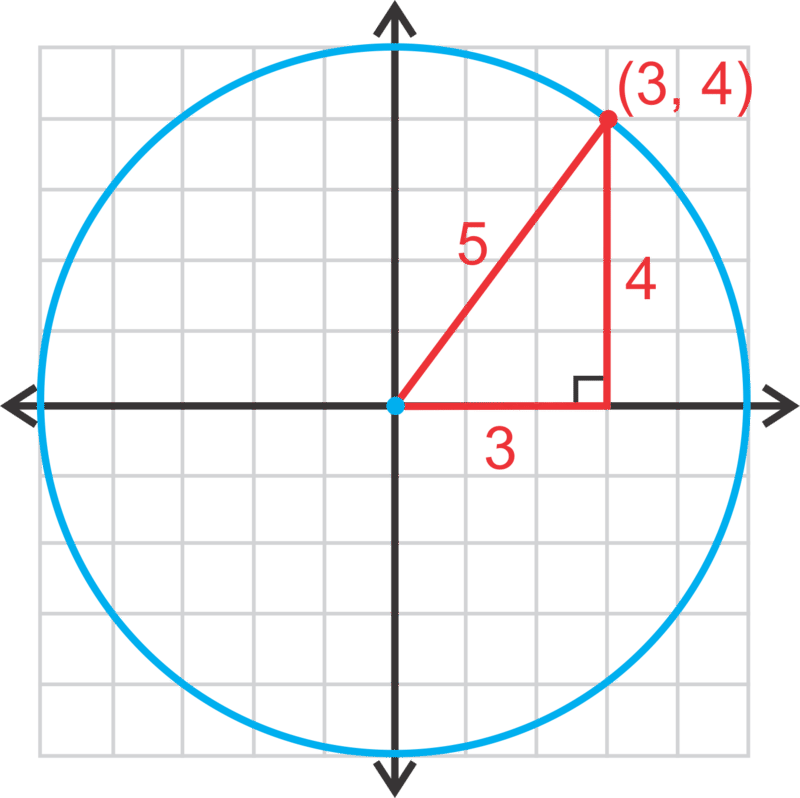
f-d_a422e8f58ba330c8e20238ba1f5fef24d986635c1b5a67f1a4482273+image_tiny+image_tiny.png

Paso 2: Usando la longitud de cada lado del triángulo rectángulo, mostrar que el Teorema de Pitágoras es cierto.

Paso 3: Ahora, en lugar de usar (3, 4), cambia el punto a (x, y) para que represente cualquier punto del círculo. Usando r para representar el radio, reescribe el Teorema de Pitágoras.

La ecuación de un círculo, centrada en el origen, es\(\ x^{2}+y^{2}=r^{2}\), donde r es el radio y (x, y) es cualquier punto del círculo.

Encontremos el radio de\(\ x^{2}+y^{2}=16\) y graficemos.

Para encontrar el radio, podemos establecer\(\ 16=r^{2}\), haciendo\(\ r=4\). \(\ r\)no es -4 porque es una distancia y las distancias siempre son positivas. Para graficar el círculo, comience en el origen y salga 4 unidades en cada dirección y conéctese.

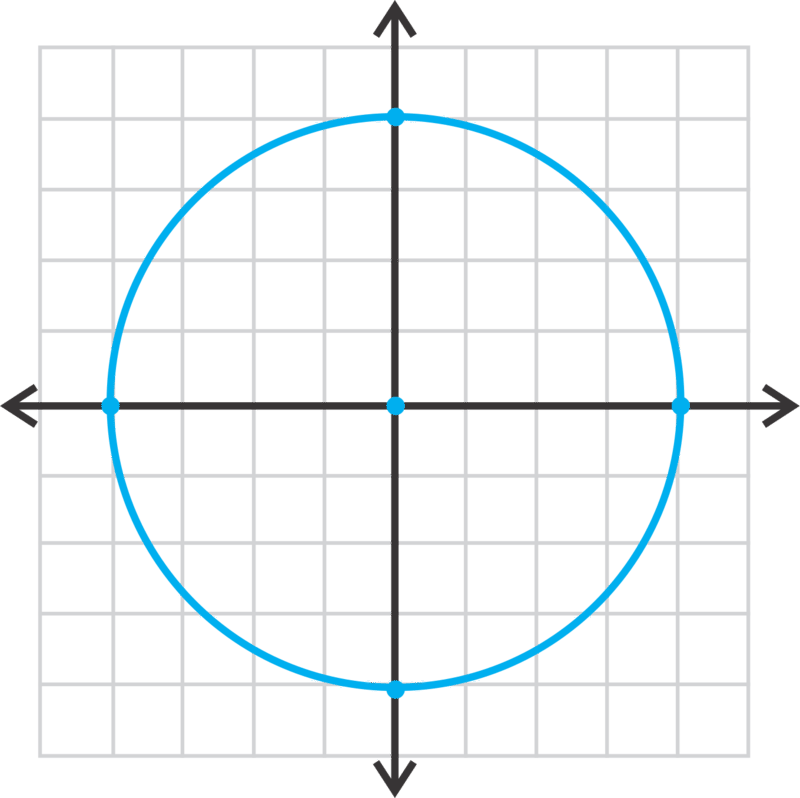
f-d_3e19a8efdc4f45e7e77b0ffd27456e06d7f6a32c875d2d748e7bc293+image_tiny+image_tiny.png

Ahora, vamos a encontrar la ecuación del círculo con el centro en el origen y pasa a través\(\ (−7,−7)\).

Usando la ecuación del círculo, tenemos:\(\ (-7)^{2}+(-7)^{2}=r^{2}\). Resolver para\(\ r^{2}\).

\ (\\ begin {alineado}
(-7) ^ {2} + (-7) ^ {2} &=r^ {2}\\
49+49 &=r^ {2}\\
98 &=r^ {2}
\ end {alineado}\)

Entonces, la ecuación es\(\ x^{2}+y^{2}=98\). El radio del círculo es\(\ r=\sqrt{98}=7 \sqrt{2}\).

Por último, determinemos si el punto\(\ (9,−11)\) está en el círculo\(\ x^{2}+y^{2}=225\).

Sustituir el punto en por x e y y ver si es igual a 225.

\ (\\ begin {alineado}
9^ {2} + (-11) ^ {2} &=225\\
81+121 &\ stackrel {?} {=} 225\\
202 &\ neq 225
\ final {alineado}\)

El punto no está en el círculo.

Ejemplos

Ejemplo 1

Anteriormente, se le pidió determinar si el punto (14 ,8) se encuentra en el círculo que está centrado en el origen y tiene un diámetro de 32 unidades.

Solución

A partir de esta lección, se sabe que la ecuación de un círculo que se centra en el origen es\(\ x^{2}+y^{2}=r^{2}\), dónde\(\ r\) está el radio y\(\ (x,y)\) es cualquier punto del círculo.

Con el punto\(\ (14,8)\),\(\ x=14\) y\(\ y=8\). Se nos da el diámetro, pero necesitamos el radio. Recordemos que el radio es la mitad del diámetro, por lo que el radio es\(\ \frac{32}{2}=16\).

Enchufa estos valores en la ecuación del círculo. Si resultan en una declaración verdadera, el punto se encuentra en el círculo.

\ (\\ begin {array} {r}
x^ {2} +y^ {2} =r^ {2}\\
14^ {2} +8^ {2}\ stackrel {?} {=} 16^ {2}\\
196+64\ stackrel {?} {=} 256\\
260\ neq 256
\ fin {matriz}\)

Por lo tanto, el punto no se encuentra en el círculo.

Ejemplo 2

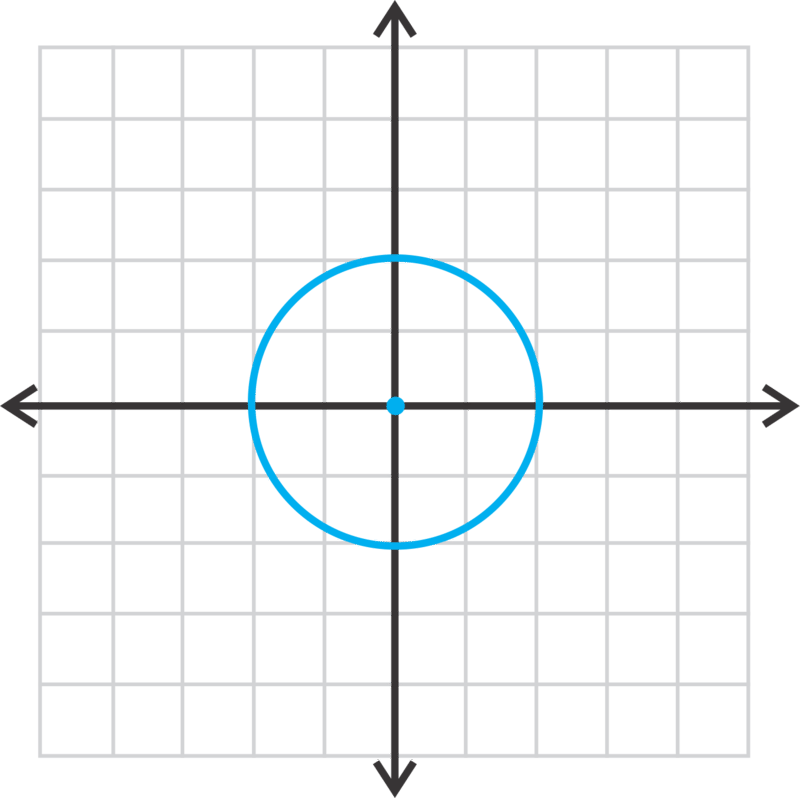
Grafica y encuentra el radio de\(\ x^{2}+y^{2}=4\).

Solución

\(\ r=\sqrt{4}=2\)

f-d_d00900a58ec8836d751020baa0f473994584a28d3837a33ec139e402+image_tiny+image_tiny.png

Ejemplo 3

Encuentra la ecuación del círculo con un radio de\(\ 6 \sqrt{5}\).

Solución

Enchufe\(\ 6 \sqrt{5}\) para\(\ r\)\(\ x^{2}+y^{2}=r^{2}\)

\ (\\ begin {array} {l}
x^ {2} +y^ {2} =( 6\ sqrt {5}) ^ {2}\
x^ {2} +y^ {2} =6^ {2}\ cdot (\ sqrt {5}) ^ {2}\
x^ {2} +y^ {2} =36\ cdot 5\
x^ {2} +y^ {2} =180
\ end {array}\)

Ejemplo 4

Encuentra la ecuación del círculo que atraviesa (5, 8).

Solución

Enchufe (5, 8) para x e y, respectivamente.

\ (\\ comenzar {alineado}
5^ {2} +8^ {2} &=r^ {2}\\
25+64 &=r^ {2}\\
89 &=r^ {2}
\ end {alineado}\)

La ecuación es\(\ x^{2}+y^{2}=89\)

Ejemplo 5

Determinar si\(\ (−10, 7)\) está en el círculo\(\ x^{2}+y^{2}=149\).

Solución

Conéctate\(\ (−10, 7)\) para ver si es una ecuación válida.

\ (\\ begin {alineado}
(-10) ^ {2} +7^ {2} &=149\\
100+49 &=149
\ end {alineado}\)

Sí, el punto está en el círculo.

Revisar

Grafica los siguientes círculos y encuentra el radio.

\(\ x^{2}+y^{2}=9\)
\(\ x^{2}+y^{2}=64\)
\(\ x^{2}+y^{2}=8\)
\(\ x^{2}+y^{2}=50\)
\(\ 2 x^{2}+2 y^{2}=162\)
\(\ 5 x^{2}+5 y^{2}=150\)

Escribe la ecuación del círculo con el radio dado y centrada en el origen.

\(\ 14\)
\(\ 6\)
\(\ 9 \sqrt{2}\)

Escribe la ecuación del círculo que pasa por el punto dado y se centra en el origen.

\(\ (7,−24)\)
\(\ (2,2)\)
\(\ (−9,−10)\)

Determinar si los siguientes puntos están en el círculo,\(\ x^{2}+y^{2}=74\).

\(\ (−8,0)\)
\(\ (7,−5)\)
\(\ (6,−6)\)

Desafío En Geometría, aprendiste sobre líneas tangentes a un círculo. Recordemos que la línea tangente toca un círculo en un punto y es perpendicular al radio en ese punto, llamado punto de tangencia.

La ecuación de un círculo es\(\ x^{2}+y^{2}=10\) con punto de tangencia\(\ (−3,1)\).
1. Encuentra la pendiente del radio desde el centro hasta\(\ (−3,1)\).
2. Encuentra la pendiente perpendicular a (a). Esta es la pendiente de la línea tangente.
3. Utilice la pendiente de (b) y el punto dado para encontrar la ecuación de la línea tangente.
Repita los pasos en #16 para encontrar la ecuación de la línea tangente a\(\ x^{2}+y^{2}=34\) con un punto de tangencia de\(\ (3,5)\).

Respuestas para problemas de revisión

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.3.

El vocabulario

Término	Definición
centro	El centro de un círculo es el punto que define la ubicación del círculo. Todos los puntos del círculo son equidistantes del centro del círculo.
Círculo	Un círculo es el conjunto de todos los puntos a una distancia específica de un punto dado en dos dimensiones.
Diámetro	El diámetro es la medida de la distancia a través del centro de un círculo. El diámetro es igual al doble de la medida del radio.
Ecuación de un círculo	Si el centro de un círculo es (0, 0), entonces la ecuación del círculo es de la forma\(\ x^{2}+y^{2}=r^{2}\), donde\(\ r\) está el radio.
Radio	El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo.

Atribuciones de imagen

[Figura 1]
Crédito: Tony Webster; Robert Pernett
Fuente: https://commons.wikimedia.org/wiki/File%3ALas_Vegas_High_Roller_(20216869960).jpg; https://flic.kr/p/nQD1fo