6.4.2: Círculos no centrados en el origen
- Page ID
- 108891
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Círculos Centrados en (h, k)
Dibuja un círculo que está centrado en (−2, −2). Se mide el diámetro del círculo para ser 18 unidades. ¿El punto (4, 5) se encuentra en el círculo?
Círculos Centrados en (h, k)
Cuando un círculo está centrado en el origen, la ecuación es\(\ x^{2}+y^{2}=r^{2}\). Si reescribimos esta ecuación, usando el centro, se vería así\(\ (x-0)^{2}+(y-0)^{2}=r^{2}\). Extendiendo esta idea a cualquier punto como el centro, tendríamos\(\ (x-h)^{2}+(y-k)^{2}=r^{2}\), donde\(\ (h,k)\) esta el centro.
Encontremos el centro y radio de\(\ (x+1)^{2}+(y-3)^{2}=16\) y graficemos.
Usando la ecuación general anterior, el centro sería\(\ (-1,3)\) y el radio es\(\ \sqrt{16}\) o 4. Para graficar, trazar el centro y luego salir 4 unidades arriba, abajo, a la izquierda, y a la derecha.
Ahora, encontremos la ecuación del círculo con centro (2,4) y radio 5.
Enchufe el centro y el radio a la ecuación y simplifique.
\ (\\ begin {array} {l}
(x-2) ^ {2} + (y-4) ^ {2} =5^ {2}\\
(x-2) ^ {2} + (y-4) ^ {2} =25
\ end {array}\)
Finalmente, encontremos la ecuación del círculo con centro (6, −1) y (5, 2) está en el círculo.
En este problema, no se nos da el radio. Para encontrar el radio, debemos usar la fórmula de distancia,\(\ d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\).
\ (\\ comenzar {alineado}
r &=\ sqrt {(5-6) ^ {2} + (2- (-1)) ^ {2}}\\
&=\ sqrt {(-1) ^ {2} +3^ {2}}\
&=\ sqrt {1+9}\\
&=\ sqrt {10}
\ end {alineado}\)
Por lo tanto, la ecuación de este círculo es\(\ (x-6)^{2}+(y-(-1))^{2}=(\sqrt{10})^{2}\) o\(\ (x-6)^{2}+(y+1)^{2}=10\).
Ejemplos
Anteriormente, se le pidió que determinara si el punto (4, 5) se encuentra en el círculo.
Solución
En esta lección, aprendiste la ecuación de un círculo que está centrado en algún lugar distinto al origen\(\ (x-h)^{2}+(y-k)^{2}=r^{2}\), donde\(\ (h,k) \) está el centro.
Se nos da que el centro es\(\ (−2,−2)\), así\(\ h=−2\) y\(\ k=−2\). También se nos da el diámetro del círculo, pero necesitamos el radio. Recordemos que el radio es la mitad del diámetro, entonces\(\ r=\frac{18}{2}=9\).
Si enchufamos estos valores en la ecuación para el círculo, obtenemos:
\ (\\ begin {alineado}
(x-h) ^ {2} + (y-k) ^ {2} &=r^ {2}\\
(x- (-2)) ^ {2} + (y- (-2)) ^ {2} &=9^ {2}\
(x+2) ^ {2} + (y+2) ^ {2} &=81
\ end {alineado}\)
Ahora para encontrar si el punto\(\ (4, 5)\) se encuentra en el círculo sustituimos 4 por x y 5 por y y y vemos si la ecuación se mantiene verdadera.
\ (\\ begin {alineado}
(x+2) ^ {2} + (y+2) ^ {2} &=81\\
(4+2) ^ {2} + (5+2) ^ {2} &\ stackrel {?} {=} 81\\
6^ {2} +7^ {2} &\ stackrel {?} {=} 81\\
85 &\ neq 81
\ final {alineado}\)
Por lo tanto, el punto no se encuentra en el círculo.
Grafica\(\ (x+4)^{2}+(y+3)^{2}=25\) y encuentra el centro y el radio.
Solución
El centro es (−4, −3) y el radio es 5.
Encuentra la ecuación del círculo con centro (−8, 3) y (2, −5) está en el círculo.
Solución
Usa la fórmula de distancia para encontrar el radio.
\ (\\ comenzar {alineado}
r &=\ sqrt {(2- (-8)) ^ {2} + (-5-3) ^ {2}}\\
&=\ sqrt {10^ {2} + (-8) ^ {2}}\\
&=\ sqrt {100+64}\\
&=\ sqrt {164}
\ end {alineado}\)
La ecuación de este círculo es\(\ (x+8)^{2}+(y-3)^{2}=164\)
Los puntos finales de un diámetro de un círculo son (−3, 1) y (9, 6). Encuentra la ecuación.
Solución
En este ejemplo, no se nos da el centro ni el radio. Podemos encontrar la longitud del diámetro usando la fórmula de distancia y luego dividirlo por 2.
\ (\\ begin {aligned}
&d=\ sqrt {(9- (-3)) ^ {2} + (6-1) ^ {2}}\\
&=\ sqrt {12^ {2} +5^ {2}}\ quad\ quad\ quad\ quad\ quad\ text {El radio es} 13\ div 2=\ frac {13} {2}\\
&\ begin {} {l}
=\ sqrt {144+25}\\
=\ sqrt {169} =13
\ end { array}
\ end {alineado}\)
Ahora, tenemos que encontrar el centro. Utilice la fórmula de punto medio con los puntos finales.
\ (\\ comenzar {alineado}
c &=\ izquierda (\ frac {-3+9} {2},\ frac {1+6} {2}\ derecha)\\
&=\ izquierda (3,\ frac {7} {2}\ derecha)
\ end {alineado}\)
Por lo tanto, la ecuación es\(\ (x-3)^{2}+\left(y-\frac{7}{2}\right)^{2}=\frac{169}{4}\).
Revisar
Para las preguntas 1-4, haga coincidir la ecuación con la gráfica.
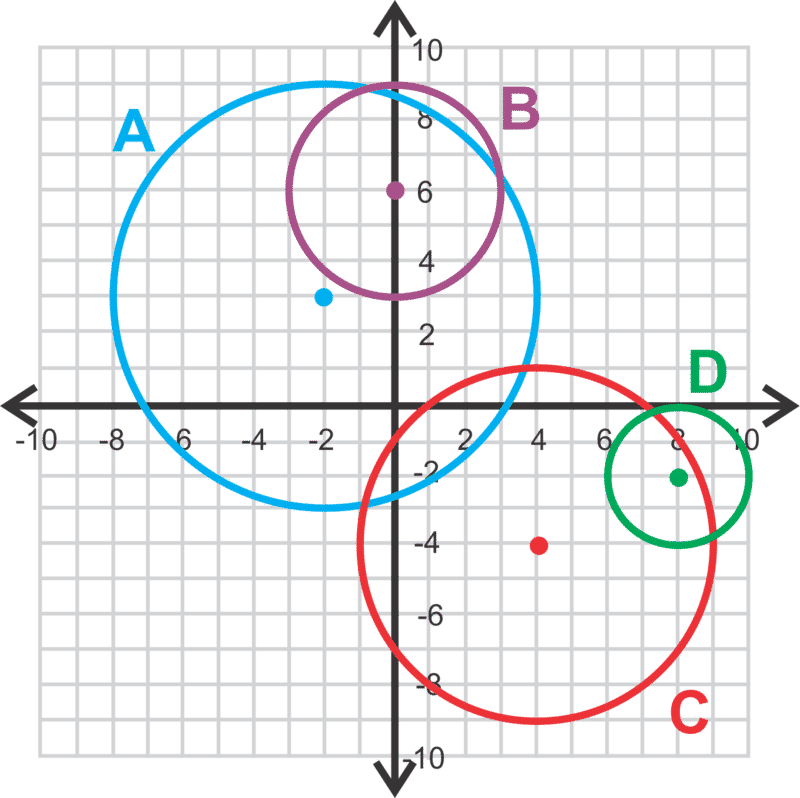
- \(\ (x-8)^{2}+(y+2)^{2}=4\)
- \(\ x^{2}+(y-6)^{2}=9\)
- \(\ (x+2)^{2}+(y-3)^{2}=36\)
- \(\ (x-4)^{2}+(y+4)^{2}=25\)
Grafica los siguientes círculos. Encuentra el centro y el radio.
- \(\ (x-2)^{2}+(y-5)^{2}=16\)
- \(\ (x+4)^{2}+(y+3)^{2}=18\)
- \(\ (x+7)^{2}+(y-1)^{2}=8\)
Encuentra la ecuación del círculo, dada la siguiente información.
- centro:\(\ (−3,−3)\) radio:\(\ 7\)
- centro:\(\ (−7,6)\) radio:\(\ \sqrt{15}\)
- centro:\(\ (8,−1)\) punto en círculo:\(\ (0,14)\)
- centro:\(\ (−2,−5)\) punto en círculo:\(\ (3,2)\)
- extremos de diámetro:\(\ (−4,1)\) y\(\ (6,3)\)
- extremos de diámetro:\(\ (5,−8)\) y\(\ (11,2)\)
- ¿Está\(\ (−9,12)\) en el círculo\(\ (x+5)^{2}+(y-6)^{2}=54\)? ¿Cómo lo sabes?
- Desafío Utilice los siguientes pasos para encontrar la ecuación de la línea tangente al círculo con el centro\(\ (3,−4)\) y el punto de tangencia\(\ (−1,8)\).
- Extensión Reescribe la ecuación del círculo,\(\ x^{2}+y^{2}+4 x-8 y+11=0\) en forma estándar completando el cuadrado tanto para los términos x como para y. Después, encuentra el centro y el radio.
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.4.
El vocabulario
| Término | Definición |
|---|---|
| Forma estándar | La forma estándar de un círculo es\(\ (x-h)^{2}+(y-k)^{2}=r^{2}\), donde\(\ (h,k)\) está el centro y\(\ r\) es el radio. |
Atribuciones de imagen
- [Figura 1]
Crédito: Tony Webster
Fuente: https://commons.wikimedia.org/wiki/File%3ALas_Vegas_High_Roller_(20216869960).jpg