6.5.1: Secciones Cónicas y Esferas de Diente de León

Última actualización
Guardar como PDF

Page ID: 108832

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Secciones Cónicas y Esferas de Diente de León

Una de las principales actividades de matemáticos y científicos de todo tipo es aprender, e intentar demostrar, cómo y por qué funcionan las cosas.

Desde la Antigua Grecia a principios del milenio, y probablemente mucho antes, se han estudiado las propiedades de las secciones cónicas. Una que se ha explorado extensamente es la “Propiedad Focal”, a la que nos hemos referido en casi todas las lecciones de esta sección.

Hay una serie de pruebas matemáticas de la propiedad focal, pero tratar de explicar tales pruebas a alguien que no dedica su vida a las matemáticas es difícil. Las esferas de diente de león son una solución.

Secciones Cónicas y Esferas de Diente de León

Esferas de diente de león y la ecuación de una elipse

No fue hasta 1822 que el matemático francés Germinal Dandelin pensó en esta construcción tan inteligente. Dandelin encontró la manera de encontrar los focos y demostrar la propiedad focal de una sola vez.

Toma la sección cónica en cuestión. Entonces elige una esfera que tenga el tamaño justo para que al caer en la cónica, toque el plano de intersección, además de quedar ajustada contra el cono por todos los lados. Si lo prefieres, puedes pensar en la esfera como un globo perfectamente redondo que se sopla hasta que “simplemente encaja” dentro del cono, aún tocando el avión. Entonces haz lo mismo al otro lado del avión. Después de haber dibujado ambas esferas tenemos esta imagen:

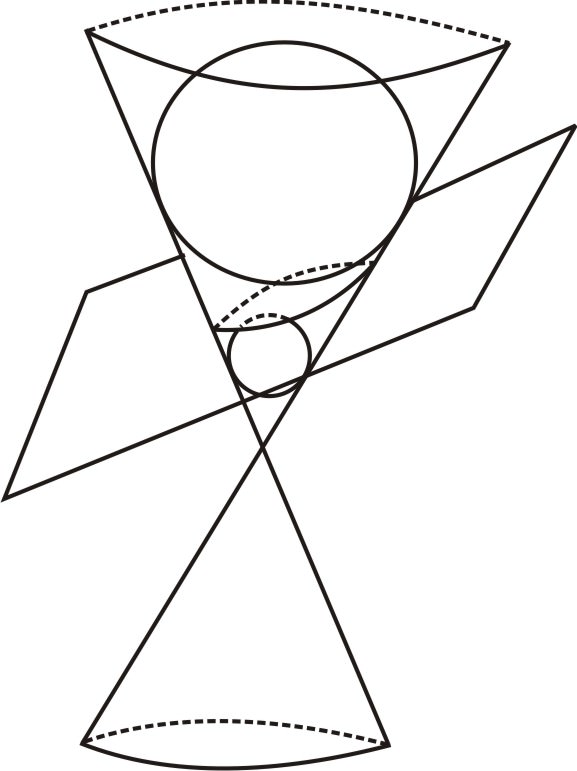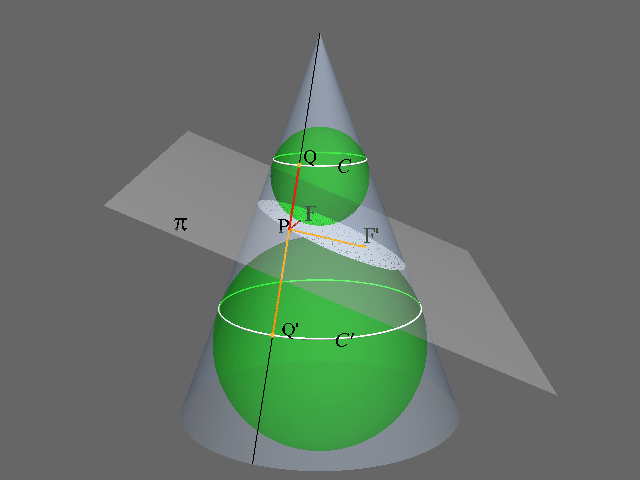
f-d_8078ff5afe3abc6cbf35e2f5dd813dc47dd19189a8a8105cc074ddd6+image_tiny+image_tiny.jpg o f-d_a3dcdfc56ba83bc2accce5a094a34161a3a52ae4636577414f4a9c9c+image_tiny+image_tiny.png

Estas esferas a menudo se llaman “esferas de diente de león”, que llevan el nombre de su descubridor. Resulta que no sólo nuestra forma es una elipse (que, como todas las elipses satisface la propiedad focal), sino que estas esferas tocan la elipse exactamente en los dos focos. Para ver esto, considera este argumento geométrico.

Lo primero que hay que notar es que los círculos\(\ C_{1}\) y\(\ C_{2}\) mostrados en el diagrama de abajo, donde cada esfera se encuentra ajustada contra el cono, se encuentran en planos paralelos entre sí. En particular, cada línea que pasa por estos círculos y el vértice del cono, como la línea\(\ l\) dibujada a continuación, corta segmentos iguales entre los dos círculos. Llamemos a\(\ d\) la distancia más corta a lo largo del cono entre círculos\(\ C_{1}\) y\(\ C_{2}\). Esto también se puede considerar como la distancia más corta entre\(\ C_{1}\) y\(\ C_{2}\) que pasa a través del vértice del cono.

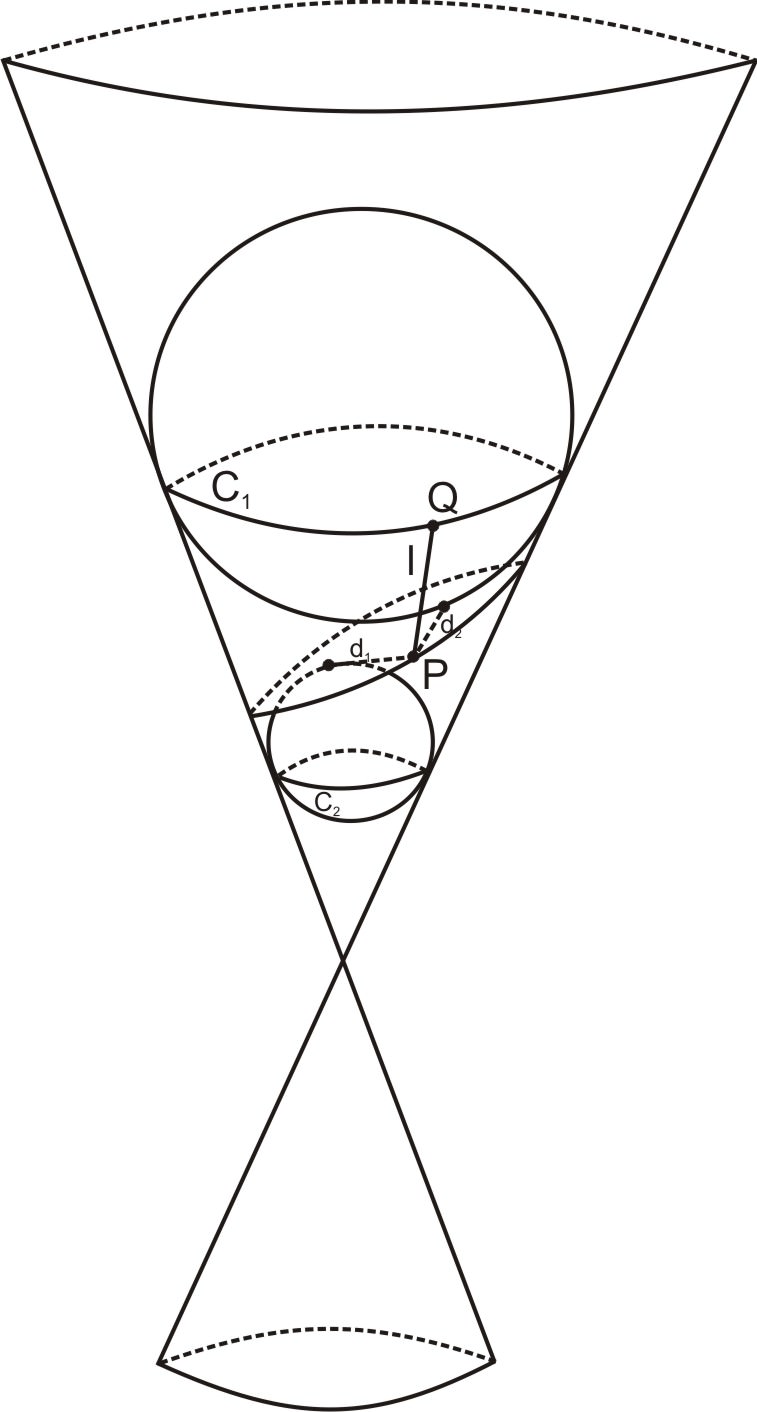
F-d_e60d18d373e0a8cbeafbd4122fff2ca2c7365ea073f3f740b995c642+image_tiny+image_tiny.jpg

Lo siguiente que debes recordar es una propiedad de las tangentes a las esferas que quizás hayas aprendido en geometría. Si se dibujan dos segmentos entre un punto y una esfera, y si la línea que contiene cada segmento es tangente a la esfera, entonces los dos segmentos son iguales. En el siguiente diagrama, AB=AC. (Esto se deduce del hecho de que las tangentes son perpendiculares a los radios de una esfera y que en esta configuración se forman dos triángulos congruentes).

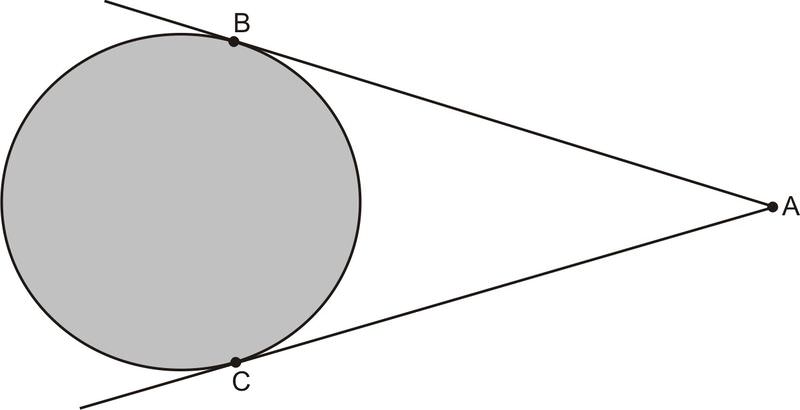
F-d_644f7b573d60f3cc338189f7d257b63dbe1aa96bbf3cd543d3d34222+image_tiny+image_tiny.jpg

Ahora considere el punto P en la elipse dibujada a continuación. Dejar\(\ \overline{Q R}\) ser el segmento de longitud\(\ d\) entre\(\ C_{1}\) y\(\ C_{2}\) que pasa por P. Las distancias entre los dos focos están marcadas\(\ d_{1}\) y\(\ d_{2}\). Pero\(\ d_{1}=R P\) y\(\ d_{2}=P Q\) por la propiedad de tangentes a esferas comentadas anteriormente. Entonces\(\ d_{1}+d_{2}=R P+P Q=Q R=d\). Y esta suma siempre será igual\(\ d\), no importa qué punto\(\ P\) de la elipse se elija. Entonces esto prueba la propiedad focal de las elipses: que la suma de las distancias entre cualquier punto de la elipse y los dos focos es constante.

F-d_e60d18d373e0a8cbeafbd4122fff2ca2c7365ea073f3f740b995c642+image_tiny+image_tiny.jpg

El diente de león y la parábola

Al igual que la elipse, la parábola tiene una propiedad focal. Y, también como la elipse, una construcción similar a la de Dandelin con las esferas puede mostrarnos lo que es. El propio Dandelin no probó la propiedad focal de las parábolas que estamos a punto de discutir, pero Pierce Morton utilizó una construcción de esfera similar a la de Dandelin para probar la propiedad focal de las parábolas en 1829. Aquí veremos el argumento de Morton.

En contraste con el argumento que hicimos para la elipse, para una parábola sólo podemos caber una esfera tangente dentro del cono. Es decir, solo una esfera puede ser tangente tanto al cono como al plano de corte. En el diagrama a continuación, la esfera encaja debajo del plano de corte, pero no hay espacio para que una esfera se encuentre encima del plano de corte y siga siendo tangente al cono.

Al igual que con la elipse, el punto donde la esfera se cruza con el plano se llama foco. Pero porque sólo hay una esfera en esta construcción, y esto está relacionado con el hecho de que una parábola tiene sólo un foco. El otro objeto geométrico de interés se llama directrix. Esta es la línea que resulta de la intersección entre el plano de corte y el plano que contiene el círculo de contacto entre la esfera y el cono. En el siguiente diagrama, la directrix se etiqueta\(\ l\) y se encuentra intersecando el plano definido por círculo\(\ C\) y el plano de corte (los planos se muestran en líneas discontinuas para mayor claridad). Por último, llamaremos al ángulo entre los planos\(\ \theta\).

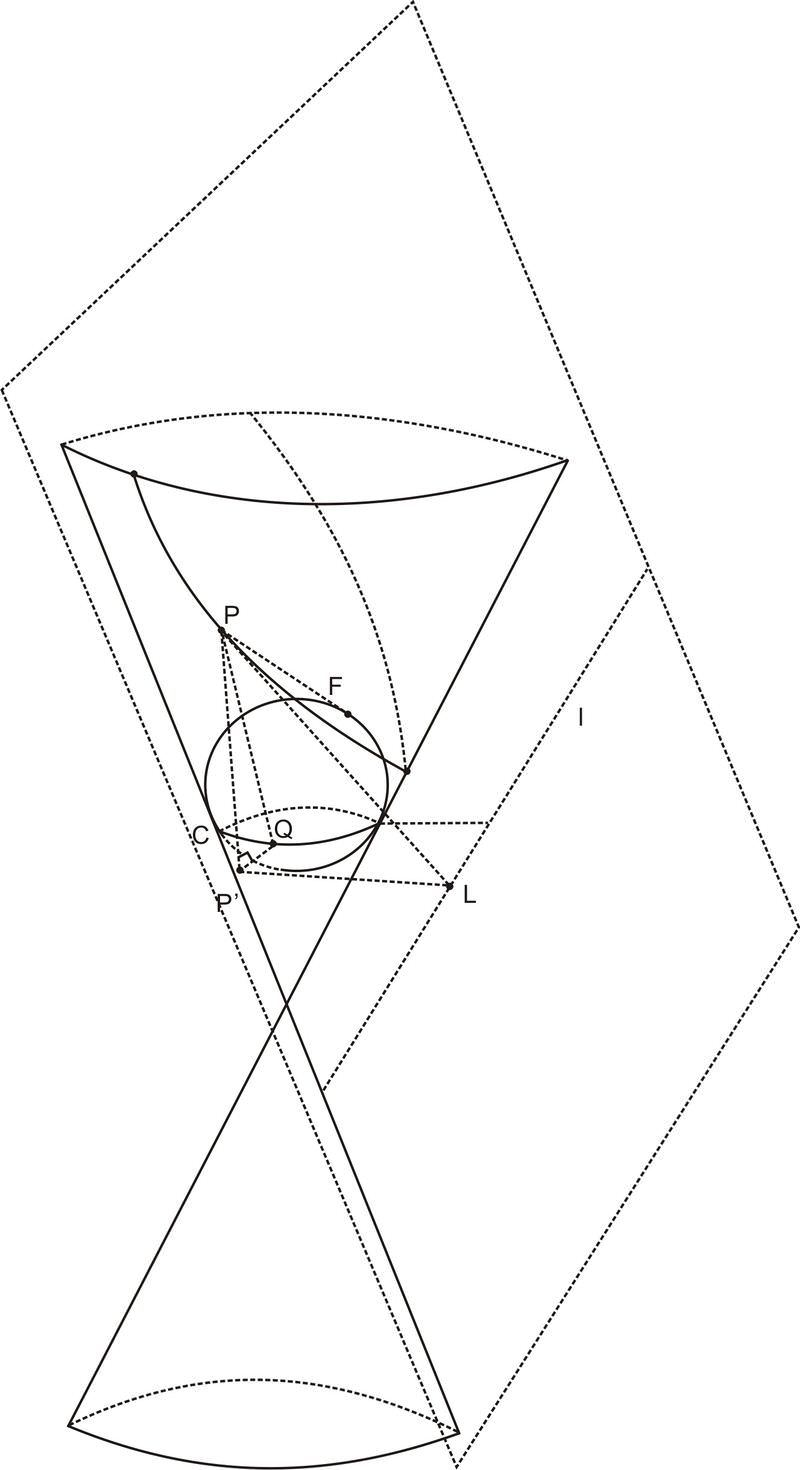
F-d_ce3523496a444c3311a1b199f0b2b521660ab4355b39a3f2840b2a83+image_tiny+image_tiny.jpg

En el diagrama anterior, hemos etiquetado el punto donde la esfera entra en contacto con el plano de corte\(\ F\), y llamaremos a ese punto el foco de la parábola. Supongamos que\(\ P\) es un punto arbitrariamente elegido sobre la parábola. Entonces, deja\(\ Q\) ser el punto sobre círculo\(\ c\) tal que\(\ \overline{P Q}\) sea tangente a la esfera. En otras palabras\(\ Q\) se elige de manera que\(\ \overline{P Q}\) yace sobre el cono mismo. Dejar\(\ L\) ser el punto en la directrix\(\ l\) tal que\(\ \overline{P L}\) sea perpendicular a\(\ l\). Entonces\(\ PF=PQ\) ya que ambos segmentos son tangentes a la esfera desde un mismo punto\(\ P\). También podemos demostrarlo\(\ PQ=PL\). Esto se deduce del hecho de que el plano de corte es paralelo a un lado del cono. Considera el punto\(\ P^{\prime}\) que es la proyección de\(\ P\) sobre el plano que contiene círculo\(\ C\). Entonces\(\ \angle P P^{\prime} Q\) y ambos\(\ \angle P P^{\prime} L\) son ángulos rectos por la definición de una proyección. \(\ \angle P Q P^{\prime}\)y ambos\(\ \angle P L P^{\prime}\) son iguales al ángulo\(\ 90-\theta\), donde\(\ \theta\) está el ángulo definido anteriormente, porque el plano de corte y el cono ambos tienen un ángulo de\(\ \theta\) con el horizonte. Ya que también comparten un lado, triángulos\(\ \triangle P Q P^{\prime}\) y\(\ \triangle P L P^{\prime}\) son congruentes por\(\ \text { AAS }\). Entonces los lados correspondientes\(\ \overline{P Q}\) y\( \overline{P L}\) son congruentes. Por la propiedad transitiva que tenemos\(\ P F=P L\), por lo que la distancia entre el punto\(\ P\) en la parábola al foco es la misma que la distancia entre\(\ P\) y la directrix\(\ l\). Acabamos de probar la propiedad focus-directrix de las parábolas.

Esferas de diente de león e hipérbolas

Para probar la propiedad focal de las hipérbolas, examinamos la construcción de la esfera de Dandelin. A diferencia de la construcción para elipses, que usaba dos esferas en un lado del cono, y la construcción de esfera para parábolas, que usaba una esfera en un lado del cono, esta construcción utiliza dos esferas, una a cada lado del cono. Al igual que con la construcción de elipse, cada esfera toca el plano en uno de los focos de la hipérbola. Y al igual que con el argumento de la propiedad focal elíptica, el argumento utiliza el hecho de que las tangentes de un punto común a una esfera son iguales.

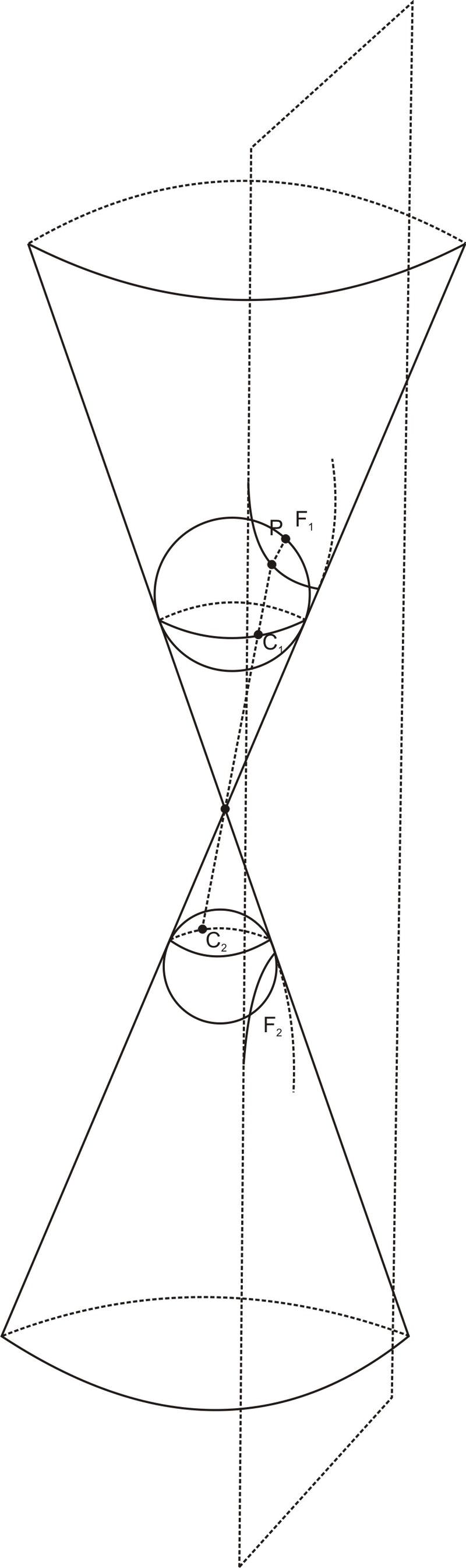
F-d_d0f71b9bd570665cc40dd2ebd3ca83349a86c938c98f1a4fcea4a134+image_tiny+image_tiny.jpg

En el diagrama anterior, supongamos que\(\ P\) es un punto arbitrario sobre la hipérbola. Nos gustaría examinar la diferencia\(\ P F_{2}-P F_{1}\). Dejar\(\ C_{1}\) ser el punto en la esfera superior que se encuentra en la línea entre\(\ P\) y el vértice del cono. Dejar\(\ C_{2}\) ser el punto en la esfera superior cuando esta línea se extiende (así\(\ P\),\(\ C_{1}\), y\(\ C_{2}\) están todos en la misma línea y\(\ P C_{1}+C_{1} C_{2}=P C_{2}\) y el cono Por la propiedad tangente común,\(\ P F_{1}=P C_{1}\) y\(\ P F_{2}=P C_{2}\) para algunos puntos\(\ C_{1}\) y\(\ C_{2}\) en los círculos donde el las esferas se encuentran con el cono. Entonces\(\ P F_{2}-P F_{1}=P C_{2}-P C_{1}=\left(P C_{1}+C_{1} C_{2}\right)-P C_{1}=C_{1} C_{2}\). Pero\(\ C_{1} C_{2}\) es la distancia a lo largo del cono entre los dos círculos de tangencia y es constante independientemente de la elección de\(\ C_{1}\) y\(\ C_{2}\). Entonces la diferencia\(\ P F_{2}-P F_{1}\) es constante.

Ejemplos

Ejemplo 1

¿Cómo serían las esferas de diente de león si se usaran para explorar un círculo?

Solución

Dado que las esferas tocan la figura dentro justo en los focos, y como un círculo es una elipse con ambos focos en el mismo punto, las esferas se sentarían directamente una encima de la otra, y tocarían el círculo en el punto central en ambos lados.

Ejemplo 2

Conceptualmente hablando, ¿por qué solo se usa una Esfera de diente de león en la prueba de una parábola?

Solución

Como aprendimos en la prueba de una elipse, la esfera de diente de león debe ser tangente tanto al cono, por ejemplo, la esfera toca el cono en todo el círculo, como al plano, donde la tangencia es un solo punto. En el caso de una parábola, la esfera debajo del plano “encaja” muy bien, pero una esfera por encima del plano “se sentaría” en el plano, y no tocaría el cono por completo. La figura sólo permite que una esfera sea tangente.

Ejemplo 3

Explique por qué para cualquier número positivo\(\ b\) y\(\ a\), existe\(\ c\) tal que\(\ b^{2}=c^{2}-a^{2}\). Let\(\ c=\sqrt{a^{2}+b^{2}}\)

Solución

Ya que siempre\(\ a^{2}+b^{2}\) es positivo para positivo\(\ a\) y\(\ b\), este número siempre se define.

Geométricamente, deja\(\ c\) ser la hipotenusa de un triángulo rectángulo con longitudes laterales\(\ a\) y\(\ b\).

Revisar

¿Quién fue el primer matemático que conceptualizó las esferas de diente de león? ¿Cuándo?
¿Qué demuestran las esferas de diente de león?
¿Cómo se identifican los focos de una elipse usando esferas de diente de león?
Si se dibujan dos tangentes de un solo punto a una esfera, ¿qué se puede decir de los segmentos de línea formados?
¿Cómo se relacionan las tangentes con un radio de una esfera?
Describir la propiedad focal de las elipses.
¿Cómo y cuándo Germinal Dandelin probó la propiedad focal de las parábolas?
¿Cuál es la línea que resulta de la intersección entre el plano de corte y el plano que contiene el círculo de contacto entre la esfera y el cono?
¿Qué se define por el punto donde la esfera se cruza con el plano de corte?
¿Qué construcción utiliza dos esferas en un solo cono?
¿Qué construcción utiliza una esfera en un solo cono?
¿Qué construcción utiliza dos esferas y dos conos?

Identifique las piezas enumeradas en el diagrama como se especifica a continuación:

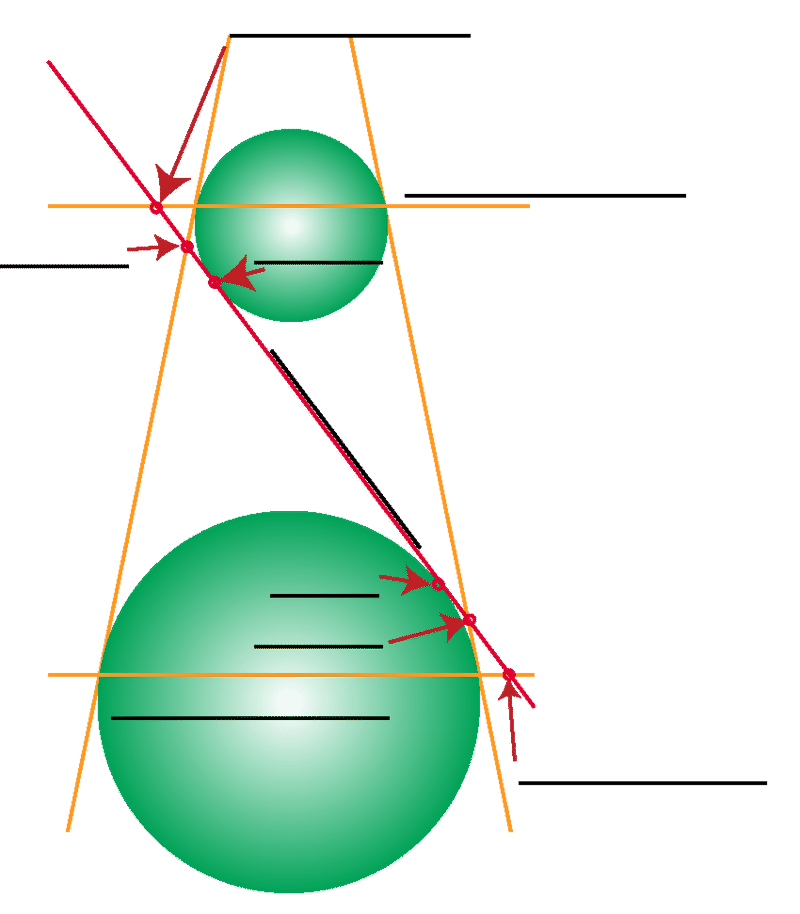
f-d_d5f9296c930624f900b480bbb9c13796c09d819bacb9d9f7d62adfcf+imagen_tiny+image_tiny.png

Línea Directrix - Esfera Pequeña
Línea Directrix - Esfera Grande
Foco - Esfera Pequeña
Foco - Esfera Grande
Vértice - Esfera Pequeña
Vértice - Esfera Grande
Plano Directrix - Esfera Pequeña
Plano Directrix - Esfera Grande
Plano de corte
¿Qué sección cónica se ilustra aquí?

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.8.

El vocabulario

Término	Definición
Cónico	Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas.
Esferas de diente de león	Las esferas de diente de león son esferas utilizadas para definir geométricamente las secciones cónicas.
Elipse	Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos.
Elipses	Las elipses son secciones cónicas que parecen círculos alargados. Una elipse representa todas las ubicaciones en dos cotas que están a la misma distancia de dos puntos especificados llamados focos.
hipérbola	Una hipérbola es una sección cónica formada cuando el plano de corte cruza ambos lados del cono, dando como resultado dos curvas infinitas en forma de “U”.
Parábola	Una parábola es el conjunto de puntos que son equidistantes de un punto fijo en el interior de la curva, llamado el “'foco"', y una línea en el exterior, llamada la “'directrix"'. La directrix es vertical u horizontal, dependiendo de la orientación de la parábola.
tangencia	Una tangencia es un punto (o conjunto de puntos) que “solo toca” una figura.