6.5.3: Cónicas Degeneradas

Última actualización
Guardar como PDF

Page ID: 108833

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Cónicas Degeneradas

La ecuación general de una cónica es\(\ A x^{2}+B x y+C y^{2}+D x+E y+F=0\). Esta forma es tan general que engloba todas las líneas regulares, puntos singulares e hipérbolas degeneradas que parecen una X. Esto se debe a que hay algunos casos especiales de cómo un plano puede intersectar un cono de dos lados. ¿Cómo se forman estas formas degeneradas?

Graficando Cónicas Degeneradas

Una cónica degenerada es una cónica que no tiene las propiedades habituales de una cónica. Las ecuaciones cónicas degeneradas simplemente no pueden escribirse en forma de gráficos. Hay tres tipos de cónicas degeneradas:

Un punto singular, que es de la forma:\(\ \frac{(x-h)^{2}}{a}+\frac{(y-k)^{2}}{b}=0\). Se puede pensar en un punto singular como un círculo o una elipse con un radio infinitamente pequeño.
Una línea, que tiene coeficientes\(\ A=B=C=0\) en la ecuación general de una cónica. La porción restante de la ecuación es\(\ D x+E y+F=0\), que es una línea.
Una hipérbola degenerada, que es de la forma:\(\ \frac{(x-h)^{2}}{a}-\frac{(y-k)^{2}}{b}=0\). El resultado son dos líneas que se cruzan que hacen una forma de “X”. Las pendientes de las líneas de intersección que forman la X son\(\ \pm \frac{b}{a}\). Esto se debe a que\(\ b\) va con la\(\ y\) porción de la ecuación y es la subida, mientras que\(\ a\) va con la\(\ x\) porción de la ecuación y es la carrera.

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó cómo se forman las cónicas degeneradas.

Solución

Cuando se interseca un plano con un cono de dos lados donde los dos conos se tocan, la intersección es un solo punto. Cuando se interseca un plano con un cono de dos lados para que el plano toque el borde de un cono, pase por el punto central y continúe tocando el borde de la otra cónica, esto produce una línea. Cuando se interseca un plano con un cono de dos lados para que el plano pase verticalmente por el punto central de los dos conos, produce una hipérbola degenerada.

Ejemplo 2

Transforme la ecuación cónica en forma estándar y boceto.

\(\ 0 x^{2}+0 x y+0 y^{2}+2 x+4 y-6=0\)

Solución

Esta es la línea\(\ y=-\frac{1}{2} x+\frac{3}{2}\)

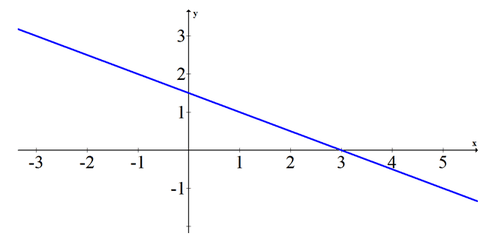
f-d_7e8667cd80d543ecc94a05f3c351d77aa5d3cf704a791fe6adf2fd99+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

Ejemplo 3

Transforme la ecuación cónica en forma estándar y boceto.

\(\ 3 x^{2}-12 x+4 y^{2}-8 y+16=0\)

Solución

\ (\\ comenzar {alineado}
3 x^ {2} -12 x+4 y^ {2} -8 y+16&=0\\
3\ izquierda (x^ {2} -4 x\ derecha) +4\ izquierda (y^ {2} -2 y\ derecha) &=-16\\
3\ izquierda (x^ {2} -4 x+4\ derecha) +4\ izquierda (y^ {2} -2 y+1\ derecha) &=-16+12+4\\
3 (x-2) ^ {2} +4 (y-1) ^ {2} &=0\\
\ frac {(x-2) ^ {2}} {4} +\ frac {(y-1) ^ {2}} {3} &=0
\ end {alineado}\)

El punto (2, 1) es el resultado de esta cónica degenerada.

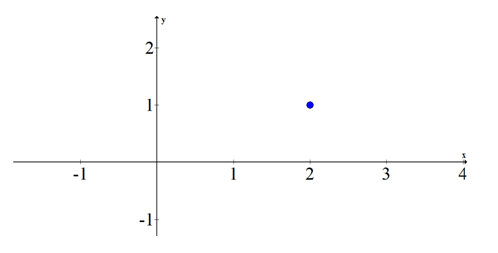
F-D_3000d08d9afd24108b4f58f18d3a2e0b38d44a71dbb721d5eae9e094+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

Ejemplo 4

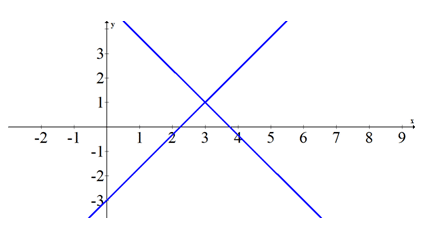
Transforme la ecuación cónica en forma estándar y boceto.

\(\ 16 x^{2}-96 x-9 y^{2}+18 y+135=0\)

Solución

\ (\\ comenzar {alineado}
16 x^ {2} -96 x-9 y^ {2} +18 y+135=0 &\\
16\ izquierda (x^ {2} -6 x\ derecha) -9\ izquierda (y^ {2} -2 y\ derecha) &=-135\\
16\ izquierda (x^ {2} -6 x+9\ derecha) -9\ izquierda (y^ {2} -2 y+1\ derecha) &=-135+144-9\\
16 (x-3) ^ {2} -9 (y-1) ^ {2} &=0\\
\ frac {( x-3) ^ {2}} {9} -\ frac {(y-1) ^ {2}} {16} &=0
\ end {alineado}\)

Se trata de una hipérbola degenerada.

f-d_1020c4e8aa8f5fece6ca7560cb3c98fd769455e9431a8fc5444f2363+image_thumb_postcard_tiny+image_thumb_postcard_tiny.png

Ejemplo 5

1. Crear una cónica que describa solo el punto (4, 7).

Solución

\(\ (x-4)^{2}+(y-7)^{2}=0\)

Revisar

¿Cuáles son las tres cónicas degeneradas?

Cambia cada ecuación en forma gráfica y establece qué tipo de cónico o degenerado es.

\(\ x^{2}-6 x-9 y^{2}-54 y-72=0\)
\(\ 4 x^{2}+16 x-9 y^{2}+18 y-29=0\)
\(\ 9 x^{2}+36 x+4 y^{2}-24 y+72=0\)
\(\ 9 x^{2}+36 x+4 y^{2}-24 y+36=0\)
\(\ 0 x^{2}+5 x+0 y^{2}-2 y+1=0\)
\(\ x^{2}+4 x-y+8=0\)
\(\ x^{2}-2 x+y^{2}-6 y+6=0\)
\(\ x^{2}-2 x-4 y^{2}+24 y-35=0\)
\(\ x^{2}-2 x+4 y^{2}-24 y+33=0\)

Esboza cada cónica o cónica degenerada.

\(\ \frac{(x+2)^{2}}{4}+\frac{(y-3)^{2}}{9}=0\)
\(\ \frac{(x-3)^{2}}{9}+\frac{(y+3)^{2}}{16}=1\)
\(\ \frac{(x+2)^{2}}{9}-\frac{(y-1)^{2}}{4}=1\)
\(\ \frac{(x-3)^{2}}{9}-\frac{(y+3)^{2}}{4}=0\)
\(\ 3 x+4 y=12\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.6.

El vocabulario

Término	Definición
Cónico	Las secciones cónicas son aquellas curvas que se pueden crear por la intersección de un doble cono y un plano. Incluyen círculos, elipses, parábolas e hipérbolas.
degenerado cónico	Una cónica degenerada es una cónica que no tiene las propiedades habituales de una sección cónica. Dado que algunos de los coeficientes de la ecuación cónica general son cero, la forma básica de la cónica es meramente un punto, una línea o un par de líneas que se cruzan.
hipérbola degenerada	Una hipérbola degenerada es un ejemplo de una cónica degenerada. Su ecuación toma la forma\(\ \frac{(x-h)^{2}}{a}-\frac{(y-k)^{2}}{b}=0\). Parece dos líneas que se cruzan que hacen una forma de “X”.

Atribuciones de imagen

[Figura 1]
Crédito: Fundación CK-12
Licencia: CC BY-SA