7.6.2: Encontrar el término n dado dos términos para una secuencia aritmética
- Page ID
- 108913
Encontrar el enésimo término dado dos términos
Estás pagando un préstamo estudiantil en cuotas mensuales. Después de su quinto pago, su saldo restante del préstamo es de $17,500. Después de su 16º pago, su saldo restante es de $12,000. ¿Cuál es la regla n º término para la secuencia representada por esta situación?
Encontrar el término n
Anteriormente, se nos daba la diferencia común directamente o dos términos consecutivos a partir de los cuales podíamos determinar la diferencia común. En este concepto encontraremos la diferencia común y escribiremos la regla del término n º dado dos términos cualesquiera en la secuencia.
Encontremos la diferencia común, primer término y regla de\(\ n^{t h}\) término para la secuencia aritmética en la que\(\ a_{7}=17\) y\(\ a_{20}=82\).
Comenzaremos usando el\(\ n^{t h}\) término regla para una secuencia aritmética para crear dos ecuaciones en dos variables:
\(\ a_{7}=17\), así\(\ a_{1}+(7-1) d=17\) o más simplemente:\(\ a_{1}+6 d=17\)
\(\ a_{20}=82\), así\(\ a_{1}+(20-1) d=82\) o más simplemente:\(\ a_{1}+19 d=82\)
Resuelve el sistema resultante:
\ (\\ begin {array} {r}
a_1 +6d =17 &\ not {a_1} +6d =17\\
\ subrayado {-1 (a_1+19d=82)} &\ quad\ quad\ Rightarrow\ quad\ quad\ subrayado {-\ not {a_1} -19d=-82}\\
&-13d=-65\
&d=5\ end {array}\)
Sustituyendo\(\ d\) con 5 en una de las ecuaciones que obtenemos
\ (\\ comenzar {alineado}
a_ {1} +6 (5) &=7\\
a_ {1} +30 &=17\\
a_ {1} &=-13
\ end {alineado}\)
Usando estos valores podemos encontrar la regla del término n:
\ (\\ begin {array} {l}
a_ {n} =-13+ (n-1) (5)\\
a_ {n} =-13+5 n-5\\
a_ {n} =5 n-18
\ end {array}\)
Ahora, vamos a encontrar la diferencia común, primer término y regla de\(\ n^{t h}\) término para la secuencia aritmética en la que\(\ a_{11}=-13\) y\(\ a_{40}=-71\).
Aunque este es exactamente el mismo tipo de problema que el anterior problema anterior, vamos a utilizar un enfoque diferente. Sabemos que el\(\ n^{t h}\) término regla es realmente solo usar el primer término y\(\ d\) agregarle\(\ n-1\) tiempos para encontrar el\(\ n^{t h}\) término. Vamos a usar esa idea para encontrar la diferencia común. Para llegar del\(\ 11^{t h}\) término al\(\ 40^{t h}\) término, la diferencia común se suma 40−11 o 29 veces. La diferencia en los valores del término es −71− (−13) o -58. ¿Qué hay que agregar 29 veces para crear una diferencia de -58? Podemos restar los términos y dividirlos por la diferencia en número de término para determinar la diferencia común.
\(\ \frac{-71-(-13)}{40-11}=\frac{-71+13}{29}=\frac{-58}{29}=-2 . \text { So } d=-2\)
Ahora podemos usar la diferencia común y uno de los términos para encontrar el primer término como lo hicimos anteriormente.
\ (\\ begin {alineado}
a_ {1} + (11-1) (-2) &=-13\\
a_ {1} + (-20) &=-13\\
a_ {1} &=7
\ end {alineado}\)
Escribiendo el\(\ n^{t h}\) término regla obtenemos:\(\ a_{n}=7+(n-1)(-2)=7-2 n+2=-2 n+9\).
Antes de mirar el siguiente problema para este concepto, vamos a conectar el\(\ n^{t h}\) término regla para una secuencia aritmética a la ecuación de una línea. ¿Te has dado cuenta de que el\(\ n^{t h}\) término simplificado regla\(\ a_{n}=p n+q\),, dónde\(\ p\) y\(\ q\) representar constantes, se parece un poco a\(\ y=m x+b\), la forma pendiente-interceptar de la ecuación de una línea? Exploremos por qué este es el caso usando la secuencia aritmética 1, 4, 7, 10,... Si creamos puntos dejando que la coordenada x sea el número del término y la coordenada y sea el término, obtenemos los siguientes puntos y podemos trazarlos en el plano de coordenadas como se muestra a continuación,
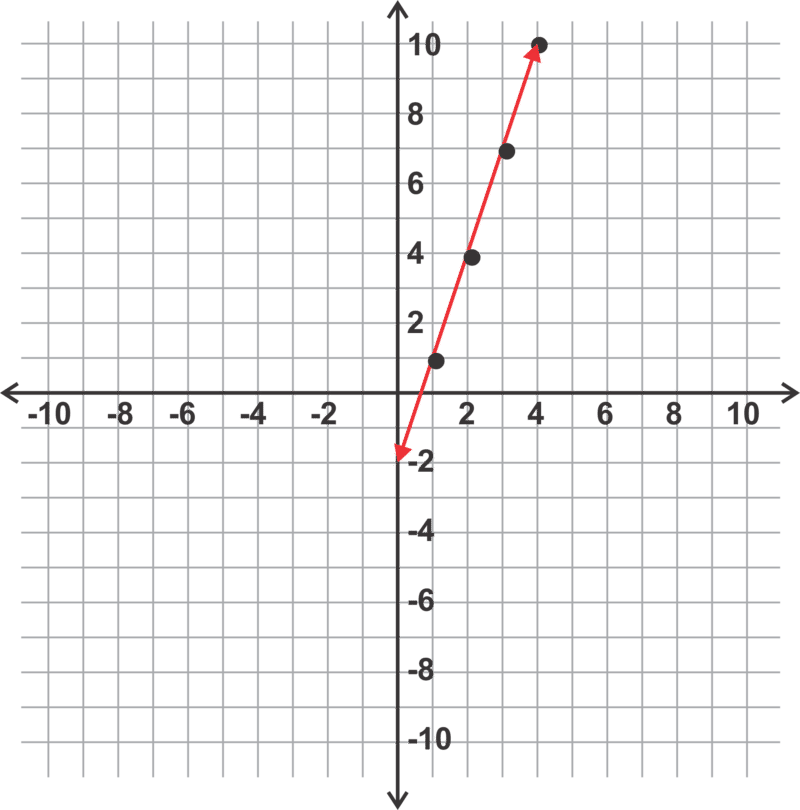
Los puntos son: (1, 1), (2, 4), (3, 7), (4, 10)
Observe, que todos estos puntos se encuentran en la misma línea. Esto sucede porque por cada incremento de uno en el término número (x), el valor del término (y) aumenta en 3. Esta diferencia común es en realidad la pendiente de la línea.
Podemos encontrar la ecuación de esta línea usando la pendiente, 3, y el punto (1, 1) en la ecuación de la\(\ y=m x+b\) siguiente manera:
\ (\\ begin {aligned}
1&=3 (1) +b\\
1&=2+b\ quad\ text {, entonces la ecuación de la línea es} y=3 x-1\\
-1&=b
\ end {alineada}\)
El\(\ n^{t h}\) término regla para la secuencia es así:\(\ a_{n}=3 n-1\).
Por último, vamos a encontrar la diferencia común, primer término y regla de\(\ n^{t h}\) término para la secuencia aritmética en la que\(\ a_{10}=-50\) y\(\ a_{32}=-182\).
Esta vez usaremos el concepto de que los términos en una secuencia aritmética son en realidad puntos en una línea para escribir una ecuación. En este caso nuestros puntos son (10, −50) y (32, −182). Podemos encontrar la pendiente y la ecuación como se muestra.
\(\ m=\frac{-182-(-50)}{32-10}=\frac{-132}{22}=-6\)
Usa el punto (10, −50) para encontrar la intercepción y:
\ (\\ begin {alineado}
-50 &=-6 (10) +b\\
-50 &=-60+b\\
10 &=b
\ end {alineado}\)
Entonces\(\ y=-6 x+10\) y\(\ a_{n}=-6 n+10\).
Ejemplos
Anteriormente, se le pidió que encontrara la regla de\(\ n^{t h}\) término para la secuencia representada por la situación del préstamo estudiantil.
Solución
En este caso nuestros puntos son (5, 17, 500) y (16, 12, 000). Podemos encontrar la pendiente y la ecuación como se muestra.
\(\ m=\frac{12,000-17,500}{16-5}=\frac{-5500}{11}=-500\)
Usa el punto (5, 17, 500) para encontrar la intercepción y:
\ (\\ begin {array} {l}
17.500=-500 (5) +b\\
17.500=-2500+b\\
20.000=b
\ end {array}\)
Entonces\(\ y=-500 x+20,000\) y\(\ a_{n}=-500 n+20,000\).
Encuentra el\(\ n^{t h}\) término regla para la secuencia aritmética con\(\ a_{6}=-13\) y\(\ a_{15}=-40\).
Solución
De\(\ a_{6}=-13\) nosotros obtenemos la ecuación\(\ a_{1}+(6-1) d=a_{1}+5 d=-13\).
De\(\ a_{15}=-40\) nosotros obtenemos la ecuación\(\ a_{1}+(15-1) d=a_{1}+14 d=-40\).
Utilice las dos ecuaciones para resolver para\(\ a_{1}\) y\(\ d\):
\ (\\ begin {array} {r}
a_1+5d=-13& a_1+5 (-3) =-13\\
\ subrayado {-a_1-14d=40} &\ text {Usado} d\ text {para encontrar} a_1\ Rightarrow\ quad\ quad\ quad a_1-15=-13\
-9d=17 & a_1=2\
d=-3
\ end {array}\)
Encuentra el\(\ n^{t h}\) término regla:\(\ a_{n}=2+(n-1)(-3)=2-3 n+3=-3 n+5\).
Encuentra el\(\ n^{t h}\) término regla para la secuencia aritmética con\(\ a_{6}=13\) y\(\ a_{22}=77\).
Solución
La diferencia común es\(\ \frac{77-13}{22-6}=\frac{64}{16}=4\). El primer término se puede encontrar usando\(\ a_{6}=13\):
\ (\\ begin {alineado}
a_ {1} + (6-1) (4) &=13\\
a_ {1} +20 &=13\\
a_ {1} &=-7
\ end {alineado}\)
Así\(\ a_{n}=-7+(n-1)(4)=-7+4 n-4=4 n-11\).
Encuentra el\(\ n^{t h}\) término regla para la secuencia aritmética con\(\ a_{7}=-75\) y\(\ a_{25}=-273\).
Solución
De\(\ a_{7}=-75\) nosotros obtenemos el punto\(\ (7,-75)\). De\(\ a_{25}=-273\) nosotros obtenemos el punto\(\ (25,-273)\).
La pendiente entre estos puntos es\(\ \frac{-273-(-75)}{25-7}=\frac{-198}{18}=-11\)
La intercepción y se puede encontrar a continuación usando el punto\(\ (7,-75)\):
\ (\\ begin {alineado}
-75 &=-11 (7) +b\\
-75 &=-77+b\\
2 &=b
\ end {alineado}\)
La ecuación final es\(\ y=-11 x+2\) y el\(\ n^{t h}\) término regla es\(\ a_{n}=-11 n+2\).
Revisar
Utilice los dos términos dados para encontrar una regla de\(\ n^{t h}\) término para la secuencia.
- \(\ a_{7}=-17\)y\(\ a_{25}=-71\)
- \(\ a_{11}=23\)y\(\ a_{42}=85\)
- \(\ a_{3}=-6\)y\(\ a_{12}=-3\)
- \(\ a_{8}=24\)y\(\ a_{2}=9\)
- \(\ a_{6}=-27\)y\(\ a_{10}=-47\)
- \(\ a_{4}=37\)y\(\ a_{12}=85\)
- \(\ a_{13}=-20\)y\(\ a_{30}=-54\)
- \(\ a_{3}=23\)y\(\ a_{9}=65\)
- \(\ a_{30}=-31\)y\(\ a_{45}=-46\)
- \(\ a_{5}=25\)y\(\ a_{11}=73\)
- \(\ a_{10}=-2\)y\(\ a_{25}=-14\)
- \(\ a_{16}=14\)y\(\ a_{28}=23\)
- \(\ a_{2}=4 n+3\)y\(\ a_{19}=4 n+65\)
- \(\ a_{10}=-3 n+7\)y\(\ a_{23}=-3 n-16\)
- ¿Qué método prefieres? ¿Por qué?
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.6.

