8.2.2: Tasas de Cambio Instantáneas

Tasas de cambio instantáneas

Quizás recordes la historia sobre Jim y su novia estrella de pista Becca de la lección sobre entender los límites. Los dos estaban discutiendo cómo podrían calcular su velocidad en el instante en que Jim le tomó una foto. El resultado final de la discusión fue Becca señalando que no es técnicamente posible calcular la velocidad exacta de algo en un instante específico.

A estas alturas, hemos explorado los conceptos relacionados de límites y líneas tangentes a una curva, por lo que sabemos que es posible calcular efectivamente la velocidad instantánea. ¿Qué proceso estaría involucrado para calcular realmente la velocidad de Becca en el instante en que se tomó la foto? ¿Cuáles son las dificultades técnicas para identificar la velocidad instantánea?

---

Tasas de cambio instantáneas

La función f′ (x) que definimos en lecciones anteriores es tan importante que tiene su propio nombre: la derivada.

La Derivada La función f' se define por la fórmula \(\ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) donde f' se llama la derivada de f con respecto a x. El dominio de f consiste en todos los valores de x para los que existe el límite.

Con base en la discusión que hemos tenido en la sección anterior, la derivada f′ representa la pendiente de la línea tangente en el punto x. Otra forma de interpretar sería que la función y = f (x) tiene una derivada f′ cuyo valor en x es la velocidad instantánea de cambio de y con respecto al punto x.

Uno de los dos conceptos primarios del cálculo consiste en calcular la tasa de cambio de una cantidad con respecto a otra. Por ejemplo, la velocidad se define como la tasa de desplazamiento con respecto al tiempo. Si una persona recorre 120 millas en 4 horas, su velocidad es de 120/4 = 30 mi/h. A esta velocidad se le llama la velocidad promedio o la tasa promedio de cambio de distancia con respecto al tiempo. Por supuesto la persona que recorre 120 millas a una tasa de 30 mi/hr por 4 hr probablemente no lo haga continuamente. Aunque probablemente bajó la velocidad o aceleró durante el periodo de 4 horas, generalmente es suficiente decir que viajó durante 4 horas a una tasa promedio de 30 millas por hora. No obstante, si el conductor golpea un árbol, no sería su velocidad promedio la que determina su supervivencia sino su velocidad al instante de la colisión. De igual manera, cuando una bala golpea un objetivo, no es la velocidad promedio la que es significativa sino su velocidad instantánea en el momento en que golpea. Entonces aquí tenemos distintos tipos de velocidades, velocidad media y velocidad instantánea.

La velocidad promedio de un objeto se define como el desplazamiento del objeto x dividido por el intervalo de tiempo ∆t durante el cual se produce el desplazamiento:

\(\ \text { Average speed }=v=\frac{\Delta x}{\Delta t}=\frac{x_{1}-x_{0}}{t_{1}-t_{0}}\)

Observe que los puntos (t ₀, x ₀) y (t ₁, x ₁) se encuentran en la curva posición versus tiempo, como muestra la siguiente figura.

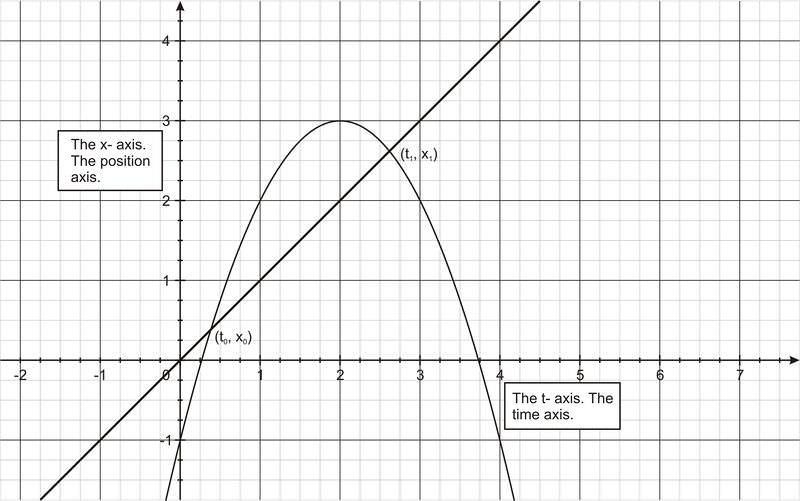
Esta expresión es también la expresión para la pendiente de una línea secante que conecta los dos puntos. Así concluimos que la velocidad promedio de un objeto entre el tiempo t ₀ y _t1 se representa geométricamente por la pendiente de la línea secante que conecta los dos puntos (t _o, x _o) y (t ₁, x ₁). Si elegimos t ₁ cerca de t _o, entonces la velocidad promedio se aproximará de cerca a la velocidad instantánea en el tiempo t _o.

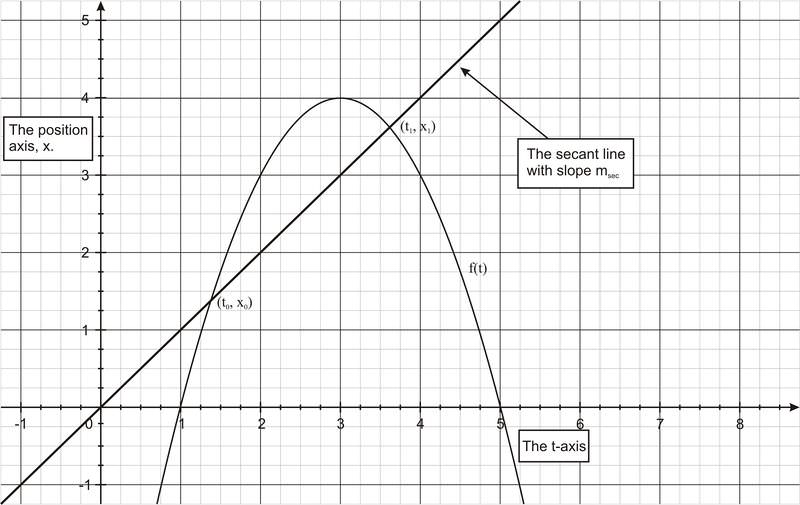
Geométricamente, la tasa promedio de cambio está representada por la pendiente de una línea secante (figura a, abajo) y la tasa instantánea de cambio se representa por la pendiente de la línea tangente (figura b, abajo).

Tasa promedio de cambio (como la velocidad promedio) La tasa promedio de cambio de y = f (x) durante el intervalo de tiempo [x 0, x 1] es la pendiente m seg de la línea secante a los puntos (x o, f (x 0)) y (x 1, f (x 0)) en la gráfica (figura a): \(\ m_{s e c}=\frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}}\)

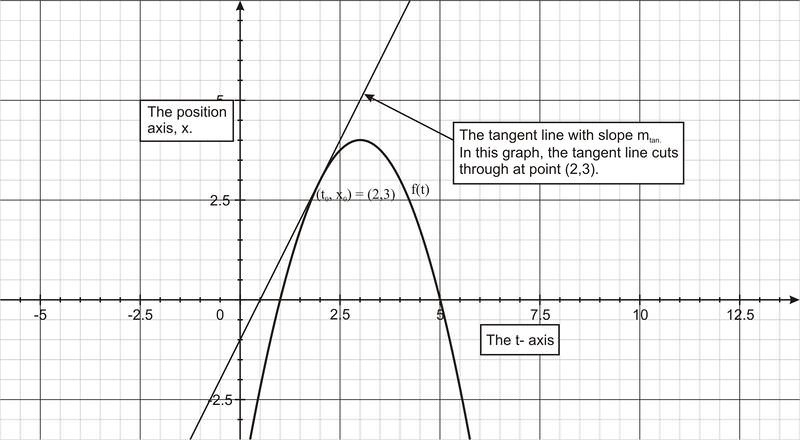
Tasa instantánea de cambio La tasa instantánea de cambio de y = f (x) en el punto x 0 es la pendiente m seg de la línea tangente al punto x 0 en la gráfica (figura b): \(\ m_{\text {tan }}=f^{\prime}\left(x_{0}\right)=\lim _{x_{1} \rightarrow x_{0}} \frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{t_{1}-t_{0}}\)

---

Ejemplos

Ejemplo 1

Anteriormente, se le hizo una pregunta sobre el proceso de calcular la velocidad de Becca en la carrera.

Solución

La velocidad es, por definición, una relación entre una distancia y el tiempo requerido para cruzar esa distancia (recuerda d=rt de tu clase de ciencias). Si el tiempo requerido es cero, entonces terminas dividiendo por cero, que es una función indefinida.

Sin embargo, usando cálculo, puede identificar cuál sería el comportamiento final de la función si se acercara infinitamente, y así calcular efectivamente la velocidad en un instante dado. De hecho, eso es exactamente lo que hiciste en los ejemplos anteriores.

Ejemplo 2

Calcular: (a) La pendiente de la línea tangente a\(\ y=x^{2}+5\) en el punto de la curva\(\ x=4\) y (b) la ecuación de esa línea.

En el concepto anterior "Tangentes a una Curva" mostramos cómo calcular la derivada (la pendiente de la tangente) de una función de la forma\(\ y=x^{2}-c\).

1. La pendiente de la tangente a la curva\(\ y=x^{2}+5\) en\(\ x=4\) es:
2. Dado\(\ m=8\) desde arriba, tenemos\(\ y=8 x+b\). Todo lo que necesitamos es resolver para que b tenga la ecuación completa.

Solución

1. \(\ 2(4)=8\)

   Recordemos del álgebra la “pendiente - forma de intercepción” de una línea recta:\(\ y=mx+b\), donde\(\ m\) está la pendiente de la línea.

2. Sustituto 4 (el punto del que estamos encontrando la pendiente) en para\(\ x\) en la ecuación de la curva

   \(\ y=x^{2}+5\)para identificar un\(\ y\)

   \(\ y=(4)^{2}+5\)

   \(\ y=21\)

   Sustituir los valores por\(\ x\)\(\ y\),, y\(\ m\) que ahora tenemos en nuestra\(\ y=mx+b\) forma de la ecuación de la línea tangente:

   \(\ 21=8(4)+b\)

   \(\ -11=b\)

   Utilice los valores calculados para\(\ m\) y\(\ b\) para completar la ecuación:

   \(\ y=8 x-11\)

Ejemplo 3

Supongamos que\(\ y=x^{2}-3\).

1. Encuentra la tasa promedio de cambio de y con respecto a x sobre el intervalo [0, 2] y
2. Encuentre la tasa instantánea de cambio de y con respecto a x en el punto x = −1.

Solución

1. Aplicando la fórmula anterior para secante con\(\ f(x)=x^{2}-3\) y\(\ x_{0}=0\) y\(\ x_{1}=2\), rendimientos

   \(\ m_{\sec }\)	\(\ =\frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{t_{1}-t_{0}}\)
   	\(\ =\frac{f(2)-f(0)}{2-0}\)
   	\(\ =\frac{1-(-3)}{2}\)
   	\(\ =2\)

   Esto significa que la tasa promedio de cambio de y es de 2 unidades por unidad de incremento en x sobre el intervalo [0, 2].

2. Recordemos, para funciones de la forma\(\ y=x^{2}+c\) que\(\ f^{\prime}(x)=2 x\left(f^{\prime}(x)\right.\) es “f primo de x”, que significa “la pendiente (m) de la línea tangente a x “)

   	m bronceado	= f′ (x 0)
   		= f′ (−1)
   		= 2 (−1)
   		= −2

   Esto significa que la tasa instantánea de cambio es negativa. Es decir, y está disminuyendo en el punto x = -1. Está disminuyendo a razón de 2 unidades por unidad de incremento en x.

Ejemplo 4

Encuentra la derivada de\(\ f(x)=\sqrt{x}\) y la ecuación de la línea tangente en x ₀ = 1.

Solución

Utilizando la definición de la derivada,

\(\ f^{\prime}(x)\)	\(\ =\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\)
	\(\ =\lim _{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h}\)
	\(\ =\lim _{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h}\left(\frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}}\right)\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{h} \frac{x+h-x}{\sqrt{x+h}+\sqrt{x}}\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{\sqrt{x+h}+\sqrt{x}}\)
	\(\ =\frac{1}{2 \sqrt{x}}\)

Así, la pendiente de la línea tangente en x ₀ = 1 es

\(\ f^{\prime}(1)\)	\(\ =\frac{1}{2 \sqrt{1}}=\frac{1}{2}\)

Para x ₀ = 1, podemos encontrar y ₀ simplemente sustituyendo en f (x):

\(\ f\left(x_{0}\right)\)	\(\ \equiv y_{0}\)
\(\ f(1)\)	\(\ =\sqrt{1}=1\)
\(\ y_{0}\)	\(\ =1\)

Así, la ecuación de la línea tangente es

\(\ y-y_{0}\)	\(\ =m\left(x-x_{0}\right)\)
\(\ y-1\)	\(\ =\frac{1}{2}(x-1)\)
\(\ y\)	\(\ =\frac{1}{2} x+\frac{1}{2}\)

Ejemplo 5

Encuentra la derivada de\(\ f(x)=\frac{x}{x+1}\).

Solución

Usando la fórmula derivada:

\(\ f^{\prime}(x)\)	\(\ =\lim _{h \rightarrow 0} \frac{\left[\frac{x+h}{x+h+1}-\frac{x}{x+1}\right]}{h}\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{x+h}{x+h+1}-\frac{x}{x+1}\right]\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{(x+h)(x+1)-x(x+h+1)}{(x+h+1)(x+1)}\right]\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{x^{2}+x+h x+h-x^{2}-x h-x}{(x+h+1)(x+1)}\right]\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{h}\left[\frac{h}{(x+h+1)(x+1)}\right]\)
	\(\ =\lim _{h \rightarrow 0} \frac{1}{(x+h+1)(x+1)}\)
	\(\ =\frac{1}{(x+1)^{2}}\)

Ejemplo 6

Un cohete es propulsado hacia arriba y alcanza una altura de\(\ h(t)=4.9 t^{2}\) en t segundos.

1. ¿Qué tan alto alcanza en 35 segundos?
2. ¿Cuál es la velocidad promedio del cohete durante los primeros 35 segundos?
3. ¿Cuál es la velocidad instantánea del cohete al final de los 35 segundos?

Solución

1. La altura del cohete a 35 segundos es\(\ 4.9(35)^{2}=6002.5 m\)
2. \(\ V_{a v g}=\frac{6002.5 m}{35 s}=171.5 \mathrm{~m} / \mathrm{s}\)
3. Para encontrar la velocidad instantánea, necesitamos encontrar la derivada de\(\ h(t)=4.9 t^{2}\)

   \(\ h^{\prime}(t)=9.8 t\)Usando la fórmula instantánea de tasa de cambio desde arriba

   \(\ 9.8 \cdot 35 s=343 \mathrm{~m} / \mathrm{sec}\)

Ejemplo 7

Una partícula se mueve en la dirección positiva a lo largo de una línea recta para que después de t nanosegundos, su distancia recorrida sea dada por\(\ \chi(t)=9.9 t^{3}\) nanómetros.

1. ¿Cuál es la velocidad promedio de la partícula durante los primeros 2 nanosegundos?
2. ¿Cuál es la velocidad instantánea de la partícula a t = 2 nanosegundos?

Solución

1. La partícula se mueve\(\ 9.9 t^{3} n m\) en\(\ t\) segundos

   \(\ \therefore 9.9\left(2^{3}\right)=\frac{79.2 n m}{2 s} \rightarrow \frac{39.6 n m}{1 s}\)

2. Usando la fórmula para encontrar el derivado, obtenemos\(\ \chi^{\prime}(t)=29.7 t^{2}\)

   \(\ \therefore \chi^{\prime}(2)=118.8 n m / s\)

   \(\ \therefore\)La velocidad instantánea a\(\ t=2\) es\(\ 118.8 \mathrm{nm} / \mathrm{sec}\)

---

Revisar

Encuentra la tasa promedio de cambio:

1. \(\ C=f(x)\)y\(\ f(x)=x^{2}-4 x+2\). Encuentra la tasa promedio de cambio de (C) con respecto a (x), cuando (x) se cambia de x = 15, a x = 59.
2. \(\ H=f(x)\)y\(\ f(x)=x^{2}-5 x+201\) Encuentra la tasa promedio de cambio de (H), con respecto a (x) cuando (x) se cambia de x = 10 a x = 11.
3. \(\ N=f(x)\)y\(\ f(x)=3 x^{2}-4 x-1\) Encontrar la tasa promedio de cambio de (N) con respecto a (x) cuando se cambia (x) se cambia de x = 20 a x = 64.
4. \(\ H=f(x)\)y f (x) =x^ {2} +10 x+201 Encuentra la tasa promedio de cambio de (H) con respecto a (x) cuando (x) se cambia de x + 25 a x = 74.
5. N=f (x) y\(\ f(x)=-5 x^{2}-3 x-4\) Encuentra la tasa promedio de cambio de (N) con respecto a (x) cuando (x) se cambia de x = 30 a x = 54.

Encuentra la tasa instantánea de cambio:

6. Si\(\ C=f(x)\) y\(\ f(x)=-4 x^{2}+2 x+5\) Encuentra la tasa instantánea de cambio de (C) con respecto a (x) cuando x = 25.
7. Si\(\ N=f(x)\) y\(\ f(x)=3 x^{2}-x-5\) Encuentra la tasa instantánea de cambio de (N) con respecto a x cuando x = 10.
8. \(\ H=f(x)\)y\(\ f(x)=4 x^{2}+195\) Encuentre la tasa instantánea de cambio de (H) con respecto a x cuando x = 10.
9. \(\ N=f(x)\)y\(\ f(x)=-x^{2}+x-3\) Encuentre la tasa instantánea de cambio de (N) con respecto a x cuando x = 150.
10. \(\ C=f(x)\)y\(\ f(x)=-3 x^{2}+4 x-4\) Encuentre la tasa instantánea de cambio de (N) con respecto a x cuando x = 20.

Usa la definición de la derivada para encontrar f (x) y luego encontrar la ecuación de la línea tangente en x = x ₀.

11. \(\ f(x)=6 x^{2} ; x_{0}=3\)
12. \(\ f(x)=\sqrt{x+2} ; x_{0}=8\)
13. \(\ f(x)=3 x^{3}-2 ; x_{0}=-1\)
14. \(\ f(x)=\frac{1}{x+2} ; x_{0}=-1\)
15. \(\ f(x)=a x^{2}-b\), (donde a y b son constantes); x ₀ = b
16. \(\ f(x)=x^{1 / 3} ; x_{0}=1\)
17. Supongamos que f tiene la propiedad de que f (x + y) = f (x) + f (y) + 3 xy y\(\ \lim _{h \rightarrow 0} \frac{f(h)}{h}=4\). Encontrar\(\ f(0)\) y\(\ f^{\prime}(x)\).
18. Encuentra\(\ d y / d x\)

Resolver los problemas de tasa de cambio.

19. Una empresa de empaque en el sur elabora “Mama's Spaghetti Sauce”. El costo de producir x tarros es de J = f (x) dólares. ¿Qué significa f' (100) = 9999 en este contexto?
20. Un pastel de cereza se toma de un horno cuando su temperatura es de 202°F y se coloca sobre una mesa en una habitación donde la temperatura es de 75°F La temperatura del pastel sobre x minutos viene dada por T = f (x). ¿Qué significa f' (100) = 102 en este contexto?
21. El número de virus, después de (x) horas, en un experimento de laboratorio controlado es V = f (x). ¿Cuáles son las unidades de f' (x)?
22. El número de personas en EU afectadas por el resfriado común en el mes de noviembre se define por N = f (x) donde x es el día del mes. ¿Cuál es el significado de f' (x) en este contexto?
23. El número de hogares en Florida afectados por la temporada de huracanes en el mes de julio se define por J = f (x) donde x es el día del mes. \(\ f(x)=2 x^{2}+x+1\)Encuentra la tasa promedio de cambio de J con respecto a x cuando los días se cambian de x = 5 a x = 34.
24. Se toma una torta de un horno cuando su temperatura es de 196°F y se coloca en una rejilla de enfriamiento en una habitación donde la temperatura es de 75°F. La temperatura de la torta durante (x) minutos viene dada por H = f (x). \(\ f(x)=4 x^{2}+15 x+196\)Encuentra la tasa instantánea de cambio de H con respecto a x cuando x = 15.
25. Se toma una sartén de pastel de carne de un horno cuando su temperatura es de 205°F y se coloca sobre una mesa en una habitación donde la temperatura es de 75°F. La temperatura del pastel de carne sobre x minutos viene dada por H = f (x). \(\ f(x)=2 x^{2}+5 x+205\). Encuentra la tasa promedio de cambio de H con respecto a x cuando los minutos se cambian de x = 5 a x = 54.

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.8.

---

vocabulario

Término	Definición
Tasa promedio de cambio	La tasa promedio de cambio de una función es el cambio en las coordenadas y de una función, dividido por el cambio en las coordenadas x.
Velocidad media	La velocidad promedio de un objeto es la distancia que recorre un objeto dividida por el tiempo de viaje
derivado	La derivada de una función es la pendiente de la línea tangente a la función en un punto dado de la gráfica. Las notaciones para derivados incluyen\(\ f^{\prime}(x), \frac{d y}{d x}, y^{\prime}, \frac{d f}{d x}\) y\(\ \frac{df(x)}{dx}\).
tasa instantánea de cambio	La tasa instantánea de cambio de una curva en un punto dado es la pendiente de la línea tangente a la curva en ese punto.
Velocidad instantánea	La velocidad instantánea de un objeto es la velocidad del objeto en un punto específico en el tiempo.
límite	Un límite es el valor que la salida de una función se acerca a medida que la entrada de la función se acerca a un valor dado.
línea secante	Una línea secante es una línea que une dos puntos en una curva.
Talud	La pendiente es una medida de la inclinación de una línea. Una línea puede tener pendiente positiva, negativa, cero (horizontal) o indefinida (vertical). La pendiente de una línea se puede encontrar calculando “subida sobre carrera” o “el cambio en la y sobre el cambio en la x”. El símbolo para la pendiente es m
Línea tangente	Una línea tangente es una línea que “solo toca” una curva en un solo punto y ningún otro.