8.2.1: Tangentes a una curva
- Page ID
- 108698
Tangentes a una curva
Kevin está aprendiendo sobre la base del cálculo y para qué se utiliza realmente el cálculo. Desafortunadamente, Kevin no entiende por qué el cálculo a veces es necesario para encontrar la ecuación de una línea. En Álgebra 1, aprendió que puedes encontrar la ecuación de una línea si te dan dos puntos. Encuentras la pendiente de la línea dividiendo la diferencia arriba/abajo en los puntos por la diferencia izquierda/derecha, luego usas uno de los puntos y la pendiente para encontrar la intercepción y.
El maestro de Kevin, el señor Banner, le ofreció crédito extra si podía encontrar la pendiente de una línea para los puntos (4,5) y (4,5) utilizando el método que aprendió en Álgebra 1. ¿Ves lo que hizo el señor Banner? ¿Qué va a encontrar Kevin mientras trabaja en esos problemas?
Tangentes a una curva
Recordemos del álgebra, si los puntos\(\ P\left(x_{0}, y_{0}\right)\) y\(\ Q\left(x_{1}, y_{1}\right)\) son dos puntos diferentes en la curva\(\ y=f(x)\), entonces la pendiente de la línea secante que conecta los dos puntos viene dada por
| \(\ m_{s e c}=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}} \tag{1}\) |
|---|
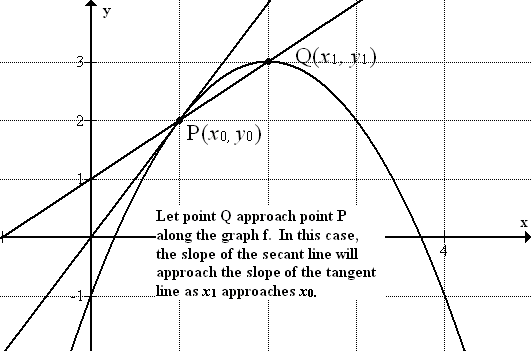
Por supuesto, si dejamos que el punto x 1 se acerque x o entonces Q se acercará a P a lo largo de la gráfica f y así la pendiente de la la línea secante se acercará gradualmente a la pendiente de la línea tangente a medida que x 1 se acerca a x 0. Por lo tanto, (1) se convierte
| \(\ m_{s e c}=\lim _{x_{1} \rightarrow x_{0}} \frac{f\left(x_{1}\right)-f\left(x_{0}\right)}{x_{1}-x_{0}} \tag{2}\) |
|---|
Para simplificar nuestra notación, si dejamos h = x 1 − x 0, entonces x 1 = x 0 + h y x 1 → x 0 se convierte en equivalente a h → 0. Esto significa que (2) se convierte
| \(\ m_{s e c}=\lim _{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}\) |
|---|
|
La pendiente de una línea tangente
siempre que exista el límite. |
|---|
Recordemos que la ecuación de la línea tangente a través del punto (x 0, y 0) con pendiente m es la forma punto-pendiente de una línea: y − y 0 = m bronceado (x − x 0).
Ejemplos
Antes, te dieron un problema sobre Kevin, quien está teniendo problemas para entender el cálculo.
Solución
El señor Banner pidió a Kevin que encontrara la ecuación de una línea dada los puntos (4, 5) y (4, 5). Los puntos (4, 5) y (4, 5) son los mismos, así que el\(\ \frac{\text { rise }}{\text { run }}\) sería\(\ \frac{0}{0}\) - ¡Kevin acaba de ser presentado a la necesidad del cálculo diferencial!
Encuentra la línea tangente a la curva\(\ f(x)=x^{3}\) que pasa por el punto P (2, 8).
Solución
Desde P (x 0, y 0) = (2, 8), usando la pendiente de la ecuación tangente tenemos
| mtan | \(\ m_{t a n}=\lim _{h \rightarrow 0} \frac{f\left(x_{0}+h\right)-f\left(x_{0}\right)}{h}\) | |
|---|---|---|
| y conseguimos | ||
| mtan | \(\ =\lim _{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}\) | |
| \(\ =\lim _{h \rightarrow 0} \frac{\left(h^{3}+6 h^{2}+12 h+8\right)-8}{h}\) | ||
| \(\ =\lim _{h \rightarrow 0} \frac{h^{3}+6 h^{2}+12 h}{h}\) | ||
| \(\ =\lim _{h \rightarrow 0}\left(h^{2}+6 h+12\right)\) | ||
| \(\ =12\) |
Así la pendiente de la línea tangente es\(\ 12\). Usando la fórmula punto-pendiente anterior, encontramos que la ecuación de la línea tangente es\(\ y-8=12(x-2)\) o\(\ y=12 x-16\).
Si\(\ f(x)=x^{2}-3\), busque\(\ f^{\prime}(x)\) y use el resultado para encontrar la pendiente de la línea tangente en\(\ x = 2\) y\(\ x = −1\).
Solución
Desde\(\ f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) entonces
| \(\ f^{\prime}(x)\) | \(\ =\lim _{h \rightarrow 0} \frac{\left[(x+h)^{2}-3\right]-\left[x^{2}-3\right]}{h}\) |
|---|---|
| \(\ =\lim _{h \rightarrow 0} \frac{x^{2}+2 x h+h^{2}-3-x^{2}+3}{h}\) | |
| \(\ =\lim _{h \rightarrow 0} \frac{2 x h+h^{2}}{h}\) | |
| \(\ =\lim _{h \rightarrow 0}(2 x+h)\) | |
| \(\ =2x\) |
Para encontrar la pendiente, simplemente sustituimos\(\ x = 2\) en el resultado\(\ f^{\prime}(x)\):
| f '(x) | = 2 x | |
|---|---|---|
| f' (2) | = 2 (2) | |
| = 4 | ||
| y | ||
| f' (x) | = 2x | |
| f' (-1) | = 2 (-1) | |
| = -2 |
Así, la pendiente de la línea tangente a x = 2 y x = −1 son 4 y −2 respectivamente.
Encuentra la pendiente de la línea tangente a la curva\(\ y=1 / x\) que pasa por el punto (1, 1).
Solución
Usando la pendiente de la fórmula tangente,
| \(\ f^{\prime}(x)\) | \(\ =\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\) | ||
|---|---|---|---|
| y sustituyendo\(\ y=\frac{1}{x}\) | |||
| \(\ f^{\prime}(x)\) | \(\ =\lim _{h \rightarrow 0} \frac{\left(\frac{1}{x+h}\right)-\frac{1}{x}}{h}\) | ||
| \(\ =\lim _{h \rightarrow 0} \frac{\frac{x-x-h}{x(x+h)}}{h}\) | |||
| \(\ =\lim _{h \rightarrow 0} \frac{x-x-h}{h x(x+h)}\) | |||
| \(\ =\lim _{h \rightarrow 0} \frac{-1}{x(x+h)}\) | |||
| \(\ =\lim _{h \rightarrow 0} \frac{-1}{x(x+h)}\) | |||
| \(\ =\frac{-1}{x^{2}}\) | |||
| Para\(\ x = 1\), la pendiente es | |||
| \(\ f^{\prime}(x)\) | \(\ =\frac{-1}{1}=-1\) | ||
| \(\ =−1\) |
Así la pendiente de la línea tangente en\(\ x = 1\) para la curva\(\ y=1 / x\) es\(\ m=-1\). Para encontrar la ecuación de la línea tangente, simplemente usamos la fórmula punto-pendiente,
| y - y 0 | = m (x - x 0) | ||
|---|---|---|---|
| Donde (x 0, y 0) = (1, 1). | |||
| y - 1 | = -1 (x - 1) | ||
| y | = - x + 1 + 1 | ||
| y | = - x + 2 |
Entonces la ecuación de la línea tangente es y = - x + 2.
Dada la función\(\ y=\frac{1}{2} x^{2}\) y los valores de\(\ x_{0}=3\) y\(\ x_{1}=4\), encontrar:
- La tasa promedio de cambio de y con respecto a x sobre el intervalo [x 0, x 1].
- La pendiente de la línea secante que conecta x 0 y x 1.
- La tasa instantánea de cambio de y con respecto a x a x 0.
- La pendiente de la línea tangente en x 1.
Solución
- Identificar los dos puntos sustituyendo 3 y 4\(\ x\) en la función\(\ f(x)=\frac{1}{2} x^{2}\)
Sustituir los dos puntos (3, 4.5) y (4, 8) en la fórmula de tasa de cambio promedio:\(\ m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\)
Tasa promedio de cambio\(\ =\frac{7}{2}\)
- La pendiente de la línea secante entre x0 y x1 es la pendiente entre (3, 4.5) y (4, 8), que es\(\ \frac{7}{2}\).
- La tasa instantánea de cambio es la pendiente a\(\ x = 3\).
Usa la fórmula:\(\ \frac{f(x+h)-f(x)}{h}\) dónde\(\ f(x)=\frac{1}{2} x^{2}\) y\(\ x=3\)
\(\ \frac{f(3+h)-f(3)}{h}\)... Sustituto\(\ 3\) de\(\ x\)
\(\ \frac{\frac{1}{2}(3+h)^{2}-\frac{1}{2}(3)^{2}}{h}\)... Reemplazar\(\ f(x) \rightarrow \frac{1}{2} x^{2}\)
\(\ \frac{\frac{1}{2}(9)+\frac{1}{2}(6 h)+\frac{1}{2} h^{2}-\frac{1}{2} 9}{h}\)... FOIL y Distribuir el 1/2
\(\ \frac{6 h+h^{2}}{2 h}\)... Simplificar
\(\ 3+\frac{h}{2}\)... Simplificar de nuevo
\(\ 3\)... Como\(\ h \rightarrow 0\)
* la pendiente instantánea en\(\ x = 3\) es\(\ 3\)
- La pendiente de la tangente a 4 es la misma que la velocidad instantánea de cambio en\(\ x=4\)
Esta es la misma serie de pasos que con\(\ x = 3\) arriba
* la pendiente en\(\ x = 4\) es\(\ 4\)
Dada la función\(\ f(x)=\frac{1}{x}\) y los valores\(\ x_{0}=2\) y\(\ x_{1}=3\), encontrar:
- La tasa promedio de cambio de y con respecto a x sobre el intervalo [x 0, x 1].
- La pendiente de la línea secante que conecta x 0 y x 1.
- La tasa instantánea de cambio de y con respecto a x a x 0.
- La pendiente de la línea tangente en x 1.
Solución
- Identificar los dos puntos sustituyendo 2 y 3 in por x en la función\(\ f(x)=\frac{1}{x}\) para obtener\(\ \left(2, \frac{1}{2}\right) \mid\left(3, \frac{1}{3}\right)\)
Sustituya los dos puntos\(\ \left(2, \frac{1}{2}\right) \mid\left(3, \frac{1}{3}\right)\) en la fórmula de tasa de cambio promedio:\(\ m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}\)
Tasa promedio de cambio\(\ =\frac{-1}{6}\)
- La pendiente de la línea secante entre\(\ x_{0}\) y\(\ x_{1}\) es la pendiente entre\(\ \left(2, \frac{1}{2}\right)\) y\(\ \left(3, \frac{1}{3}\right)\), que es\(\ \frac{-1}{6}\).
- Tasa instantánea de cambio en\(\ x_{0}\) es la pendiente en\(\ x= 2\).
Usa la fórmula:\(\ \frac{f(x+h)-f(x)}{h}\) dónde\(\ f(x)=\frac{1}{x}\) y\(\ x=2\)
\(\ \frac{f(2+h)-f(2)}{h}\)... Sustituto\(\ 2\) de\(\ x\)
\(\ \frac{\frac{1}{2+h}-\frac{1}{2}}{h}\)... Reemplazar\(\ f(x) \rightarrow \frac{1}{x}\)
\(\ \left(\frac{1}{2+h}-\frac{1}{2}\right) \cdot \frac{1}{h}\)... Tuvimos una fracción dividida por una fracción, invertir para multiplicar
\(\ \frac{(2)(1)}{2(2+h)}-\frac{(2+h)(1)}{2(2+h)} \cdot \frac{1}{h}\)... Establecer denominadores comunes
\(\ \frac{(2)-(2+h)}{(2+h)(2)(h)}\)... Simplificar
\(\ \frac{-h}{4 h+2 h^{2}}\)... Simplificar de nuevo
\(\ \frac{-1}{4+2 h}\)... una vez más (cancelando el\(\ h\))
\(\ \frac{-1}{4}\)... Como\(\ h \rightarrow 0\)
* la pendiente instantánea en\(\ x=2\) es\(\ \frac{-1}{4}\)
- La pendiente de la tangente a 3 es la misma que la velocidad instantánea de cambio en\(\ x=3\)
Esta es la misma serie de pasos que con\(\ x = 2\) arriba
* la pendiente en\(\ x = 3\) es\(\ \frac{-1}{9}\)
Revisar
- ¿Cómo se llama la línea que conecta dos puntos\(\ \left(x_{0}, y_{0}\right)\) y\(\ \left(x_{1}, y_{1}\right)\) en una curva?
- A medida que\(\ \left(x_{0}, y_{0}\right)\) se acerca inconmensurablemente\(\ \left(x_{1}, y_{1}\right)\) al término que describe la línea entre ellos se convierte en: “la línea ____________”
- La expresión\(\ f\left(x_{0}+h\right)-f\left(x_{0}\right)\) se utiliza para describir qué distancia en el proceso de encontrar la pendiente de una línea tangente?
- Al calcular la pendiente de una tangente, ¿qué valor se supone que va a 0 a medida que los dos puntos elegidos se acercan cada vez más?
- ¿Qué tiene que ver el concepto de límite, discutido en lecciones anteriores, con encontrar la pendiente de una línea tangente a una curva?
Encuentra la ecuación de la línea tangente:
- ¿Cuál es la ecuación de la línea tangente al\(\ x=−3\) asumir eso\(\ r(-3)=-5\) y\(\ r^{\prime}(-3)=1\)?
- ¿Cuál es la ecuación de la línea tangente al\(\ x=1\) asumir eso\(\ r(1)=3\) y\(\ r^{\prime}(1)=-5\)?
- ¿Cuál es la ecuación de la línea tangente al\(\ x=2\) asumir eso\(\ g(2)=1\) y\(\ g^{\prime}(2)=-3\)?
- ¿Cuál es la ecuación de la línea tangente al\(\ x=4\) asumir eso\(\ u(4)=4\) y\(\ u^{\prime}(4)=3\)?
- ¿Cuál es la ecuación de la línea tangente al\(\ x=-4\) asumir eso\(\ t(-4)=2\) y\(\ t^{\prime}(-4)=5\)?
Encuentra la ecuación de la línea tangente:
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ h(x)=-5 x^{3}-3 x^{2}+x+3\) at\(\ x=1\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ t(x)=-2 x\) at\(\ x=-2\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ m(x)=3 x^{3}+3 x^{2}+4 x+4\) at\(\ x=1\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ q(x)=-x^{3}-4 x^{2}+4 x+3\) at\(\ x=−2\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ t(x)=-4 x^{2}+2 x-4\) at\(\ x=−1\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ h(x)=-4 x^{3}+2 x^{2}-3 x+3\) at\(\ x=−1\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ m(x)=x\) at\(\ x=0\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ s(x)=-3 x^{2}-2 x+3\) at\(\ x=0\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ c(x)=-3\) at\(\ x=0\)
- Encuentra la ecuación de la línea tangente a la gráfica de\(\ b(x)=-5 x^{4}+3 x^{3}-x^{2}+5 x-3\) at\(\ x=−1\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.7.
El vocabulario
| Término | Definición |
|---|---|
| secante | Una línea que cruza un círculo en dos puntos. |
| tangente | Una línea que cruza un círculo exactamente en un punto. |
| Tasa promedio de cambio | La tasa promedio de cambio de una función es el cambio en las coordenadas y de una función, dividido por el cambio en las coordenadas x. |
| Cálculo diferencial | El cálculo diferencial es la rama del cálculo basada en encontrar la diferencia de ubicación entre dos puntos que se acercan hasta que la distancia entre ellos es infinitamente pequeña. |
| tasa instantánea de cambio | La tasa instantánea de cambio de una curva en un punto dado es la pendiente de la línea tangente a la curva en ese punto. |
| línea secante | Una línea secante es una línea que une dos puntos en una curva. |
| Talud | La pendiente es una medida de la inclinación de una línea. Una línea puede tener pendiente positiva, negativa, cero (horizontal) o indefinida (vertical). La pendiente de una línea se puede encontrar calculando “subida sobre carrera” o “el cambio en la y sobre el cambio en la x”. El símbolo de pendiente es m |
| Línea tangente | Una línea tangente es una línea que “solo toca” una curva en un solo punto y ningún otro. |

