8.5.1: Teorema Fundamental del Cálculo
- Page ID
- 108661
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Teorema Fundamental del Cálculo
La velocidad debida a la gravedad se puede calcular fácilmente mediante la fórmula: v = gt, donde g es la aceleración por gravedad (9.8m/s 2) y t es tiempo en segundos. De hecho, una aproximación decente se puede calcular en tu cabeza fácilmente redondeando 9.8 a 10 para que solo puedas agregar un decimal a la hora.
Usando esta función para la velocidad, ¿cómo podría encontrar una función que representara la posición del objeto después de un tiempo dado? ¿Qué pasa con una función que representaba la aceleración instantánea del objeto en un momento dado?
Teorema Fundamental del Cálculo
Antiderivados
Si crees que evaluar áreas bajo curvas es un proceso tedioso probablemente tengas razón. Afortunadamente, hay un método más fácil. En esta sección, daremos un método general de evaluación de integrales definidas (área bajo la curva) mediante el uso de antiderivados.
|
Definición: El Antiderivado Si F '(x) = f (x), entonces F' (x) se dice que es la antiderivada de f ( x). |
|---|
Existen reglas para encontrar las antiderivadas de funciones de potencia simples como f (x) = x 2. Al leer a través de ellos, trata de pensar por qué tienen sentido, teniendo en cuenta que la diferenciación invierte la integración.
Existen reglas para encontrar las antiderivadas de funciones de potencia simples como f (x) = x 2. Al leer a través de ellos, trata de pensar por qué tienen sentido, teniendo en cuenta que la diferenciación invierte la integración.
Reglas para encontrar los antiderivados de las funciones de poder
|
|---|
| donde k es una constante. (Observe que esta regla viene como resultado de la regla de poder anterior.) |
El teorema fundamental del cálculo
El Teorema Fundamental del Cálculo aclara la relación entre derivados e integrales. La integración realizada en una función puede ser revertida por diferenciación.
|
El teorema fundamental del cálculo Si se define una función f (x) sobre el intervalo [a, b] y si F (x) es el antidervativo de f en [a, b ], luego \ (\\ comenzar {alineado} |
|---|
Podemos utilizar la relación entre diferenciación e integración esbozada en el Teorema Fundamental del Cálculo para calcular integrales definidas más rápidamente.
Ejemplos
Evaluar\(\ \int_{1}^{2} x^{2} d x\).
Solución
Esta integral nos indica evaluar el área bajo la curva\(\ f(x)=x^{2}\), que es una parábola en el intervalo [1, 2], como se muestra en la siguiente figura.
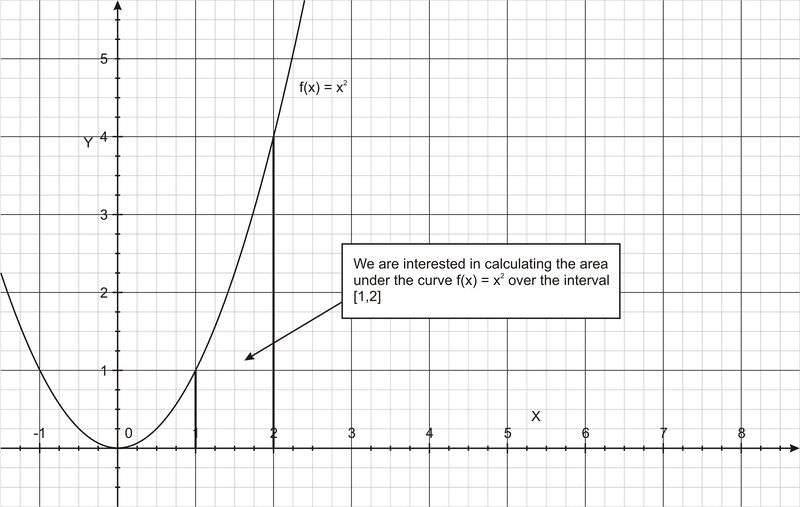
Para computar la integral según el Teorema Fundamental del Cálculo, necesitamos encontrar la antiderivada de\(\ f(x)=x^{2}\). Resulta ser\(\ F(x)=(1 / 3) x^{3}+C\), donde C es una constante de integración.
¿Cómo podemos conseguir esto? Piense en las funciones que tendrán derivadas de\(\ x^{2}\). Toma la derivada de\(\ F(x)\) para comprobar que hemos encontrado tal función. (Para reglas más específicas, vea el recuadro después de este ejemplo). Sustituyendo al Teorema Fundamental,
| \(\ \int_{a}^{b} f(x) d x\) | \(\ =\left.F(x)\right|_{a} ^{b}\) |
|---|---|
| \(\ \int_{1}^{2} x^{2} d x\) | \(\ =\left[\frac{1}{3} x^{3}+C\right]_{1}^{2}\) |
| \(\ =\left[\frac{1}{3}(2)^{3}+C\right]-\left[\frac{1}{3}(1)^{3}+C\right]\) | |
| \(\ =\left[\frac{8}{3}+C\right]-\left[\frac{1}{3}+C\right]\) | |
| \(\ =\frac{7}{3}+C-C\) | |
| \(\ =\frac{7}{3}\) |
Entonces el área bajo la curva es (7/3) unidades 2.
Evaluar\(\ \int x^{3} d x\)
Solución
Desde entonces\(\ \int x^{n} d x=\frac{1}{n+1} x^{n+1}+C\), tenemos
| \(\ \int x^{3} d x\) | \(\ =\frac{1}{3+1} x^{3+1}+C\) |
|---|---|
| \(\ =\frac{1}{4} x^{4}+C\) |
Para verificar nuestra respuesta podemos tomar la derivada de\(\ \frac{1}{4} x^{4}+C\) y verificar que es\(\ x^{3}\), la función original en nuestra integral.
Evaluar\(\ \int 5 x^{2} d x\)
Solución
Usando el múltiplo constante de una regla de potencia, el coeficiente 5 se puede eliminar fuera de la integral:
\(\ \int 5 x^{2} d x=5 \int x^{2} d x\)
Entonces podemos integrar:
| \(\ =5 \cdot \frac{1}{2+1} x^{2+1}+C\) |
|---|
| \(\ =\frac{5}{3} x^{3}+C\) |
Nuevamente, si quisiéramos revisar nuestro trabajo podríamos tomar la derivada de\(\ \frac{5}{3} x^{3}+C\) y verificar que obtenemos\(\ 5 x^{2}\).
Evaluar\(\ \int\left(3 x^{3}-4 x^{2}+2\right) d x\).
Solución
Usando la regla de suma y diferencia podemos separar nuestra integral en tres integrales:
\ (\\ begin {array} {l}
\ int\ izquierda (3 x^ {3} -4 x^ {2} +2\ derecha) d x=\\
3\ izquierda (\ int x^ {3} d x\ derecha) -4\ izquierda (\ int x^ {2} d x\ derecha) +\ izquierda (\ int 2 d x\ derecha)
\\ fila derecha 3\ cdot\ frac {1} {4} x^ {4} -4\ cdot\ frac {1} {3} x^ {3} +2 x+C\ fila derecha\ frac {3} {4} x^ {4} -\ frac {4} {3} x^ {3} +2 x+c
\ end {array}\)
Evaluar\(\ \int_{2}^{5} \sqrt{x} d x\).
Solución
La evaluación de esta integral representa calcular el área bajo la curva\(\ y=\sqrt{x}\) de\(\ x = -2\) a\(\ x = 3\), que se muestra en la siguiente figura.
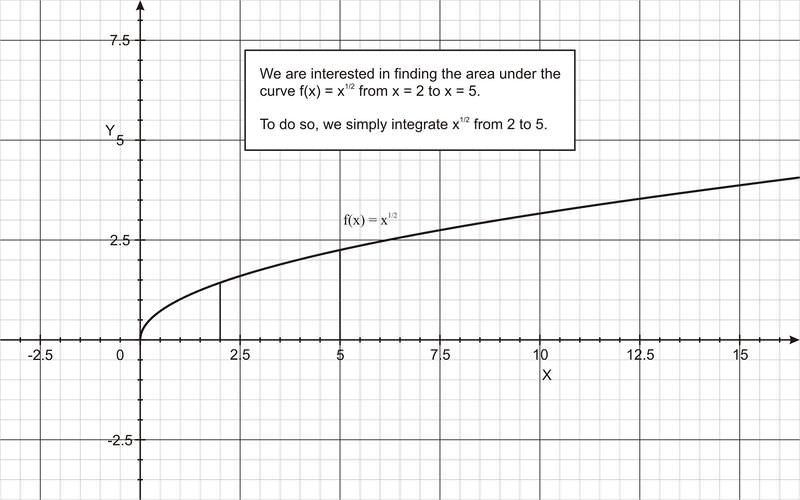
| \(\ \int_{2}^{5} \sqrt{x} d x\) | \(\ =\int_{2}^{5} x^{1 / 2} d x\) |
|---|---|
| \(\ =\left[\frac{1}{\frac{1}{2}+1} x^{1 / 2+1}\right]_{2}^{5}\) | |
| \(\ =\left[\frac{1}{3 / 2} x^{3 / 2}\right]_{2}^{5}\) | |
| \(\ =\frac{2}{3}\left[x^{3 / 2}\right]_{2}^{5}\) | |
| \(\ =\frac{2}{3}\left[5^{3 / 2}-2^{3 / 2}\right]\) | |
| \(\ =5.57\) |
Entonces el área bajo la curva es de 5.57.
Utilice el Teorema Fundamental del Cálculo para resolver:\(\ \int_{4}^{6} \frac{d x}{x}\).
Solución
Dado lo que sabemos, que si\(\ F(x)=\ln x\), entonces\(\ F^{\prime}(x)=\frac{1}{x}\)
Así, aplicamos el Teorema Fundamental del Cálculo:
\(\ \int-4^{6} \frac{d x}{x}=\ln x \mid-46\)
= F (6) - F (4) = [ln (6)] - [ln (4)] = 0.4055
Utilice el Teorema Fundamental del Cálculo para resolver:\(\ \int_{-2 p}^{2 p} 3 \cos (x) d x\).
Solución
Dado lo que sabemos, que si F (x) = 3sin (x), entonces F' (x) = 3cos (x)
Entonces aplicamos el Teorema Fundamental del Cálculo:
\(\ \int_{-2 p}^{2 p} 3 \cos d x=\left.3 \sin (x)\right|_{-2 p} ^{2 p}\)
= F (8) - F (0) = [3sin (2p)] - [3sin (-2p)] = 1 - 0 = 0
Revisar
Evaluar la integral:
- Evaluar la integral\(\ \int_{0}^{3} 5 x d x\)
- Evaluar la integral\(\ \int_{0}^{1} x^{4} d x\)
- Evaluar la integral\(\ \int_{1}^{4}(x-3) d x\)
Encuentra la integral:
- Encuentra la integral de (x + 1) (2 x - 3) de -1 a 2.
- Encuentra la integral\(\ \sqrt{x}\) de 0 a 9.
- Encuentra\(\ \int_{-1}^{0}-3 d x\)
- Encuentra\(\ \int_{-1}^{3} d x\)
- Encuentra\(\ \int_{-p}^{\frac{p}{2}}-4 \cos (x) d x\)
- Encuentra\(\ \int_{0}^{2}-d x\)
- Encuentra\(\ \int_{2}^{7} \frac{d x}{x}\)
- Encuentra\(\ \int_{-2}^{0} x+5 d x\)
- Encuentra\(\ \int_{-p}^{\frac{3 p}{2}} 6 \sin (x) d x\)
- Encuentra\(\ \int_{6}^{7} \frac{d x}{x}\)
Desafíate a ti mismo
- Croquis\(\ y=x^{3}\) y\(\ y=x\) en el mismo sistema de coordenadas y luego encontrar el área de la región encerrada entre ellos (a) en el primer cuadrante y (b) en el primer y tercer cuadrantes.
- Evaluar la integral\(\ \int_{-R}^{R}\left(\pi R^{2}-\pi x^{2}\right) d x\) donde R es una constante.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.13.
El vocabulario
| Término | Definición |
|---|---|
| antiderivado | Un antiderivado es una función que invierte una derivada. La función A es la antiderivada de la función B si la función B es la derivada de la función A. |
| derivado | La derivada de una función es la pendiente de la línea tangente a la función en un punto dado de la gráfica. Las notaciones para derivados incluyen\(\ f^{\prime}(x), \frac{d y}{d x}, y^{\prime}, \frac{d f}{d x}\) y\(\ \frac{df(x)}{dx}\). |
| teorema fundamental del cálculo | El teorema fundamental del cálculo demuestra que la integración realizada en una función puede ser revertida por diferenciación. |
| integral | Se utiliza una integral para calcular el área bajo una curva o el área entre dos curvas. |
| teorema | Un teorema es una afirmación que puede demostrarse verdadera usando postulados, definiciones y otros teoremas que ya han sido probados. |