3.3: Teorema del Valor Intermedio, Existencia de Solución
- Page ID
- 105984
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Si bien la idea de continuidad puede parecer algo básica, cuando una función es continua a lo largo de un intervalo cerrado como x∈ [1,4], en realidad se pueden sacar algunas conclusiones importantes. Las conclusiones pueden ser obvias cuando entiendes las afirmaciones y miras una gráfica, pero sin embargo son poderosas.
¿Qué se puede concluir usando el Teorema del Valor Intermedio y el Teorema del Valor Extremo sobre una función que es continua en el intervalo cerrado x∈ [1,4]?
Los Teoremas de Valor Intermedio y Extremo
El Teorema del Valor Intermedio establece que si una función es continua en un intervalo cerrado y u es un valor entre f (a) y f (b) entonces existe un c∈ [a, b] tal que f (c) =u.
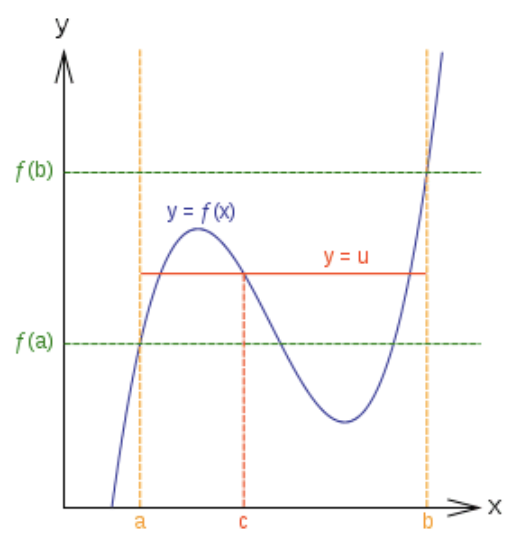
Fundación CK-12 - http://commons.wikimedia.org/wiki/File:Intermediatevaluetheorem.svg - CC BY-SA
En pocas palabras, si una función es continua entre un punto bajo y un punto alto, entonces debe valorarse en cada altura intermedia entre los puntos bajo y alto.
Lo contrario de una declaración if then es una nueva declaración con la hipótesis de la declaración original conmutada con la conclusión de la declaración original. En otras palabras, lo contrario es cuando se intercambian la parte if de la declaración y la parte entonces de la declaración. En general, no es cierto lo contrario de una afirmación.
Lo contrario del Teorema del Valor Intermedio es: Si existe un valor c∈ [a, b] tal que f (c) =u por cada u entre f (a) y f (b) entonces la función es continua.
Esta afirmación es falsa. Para mostrar que la sentencia es falsa, todo lo que necesitas es un contraejemplo donde se golpea cada valor intermedio y la función es discontinua.Un contraejemplo de una declaración if then es cuando la hipótesis (la parte if de la oración) es verdadera, pero la conclusión (la parte then de la declaración) no es cierto.
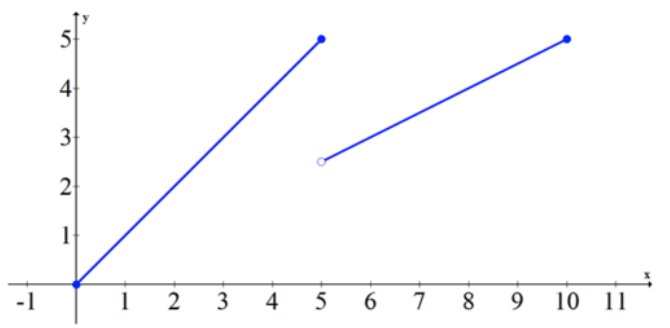
Fundación CK-12 - CC BY-SA
Esta función es discontinua en el intervalo [0,10] pero se golpea cada valor intermedio entre la primera altura en (0,0) y la altura del último punto (10,5).
El Teorema del Valor Extremo establece que en cada intervalo [a, b] donde una función es continua hay al menos un máximo y un mínimo. Es decir, debe tener al menos dos valores extremos.
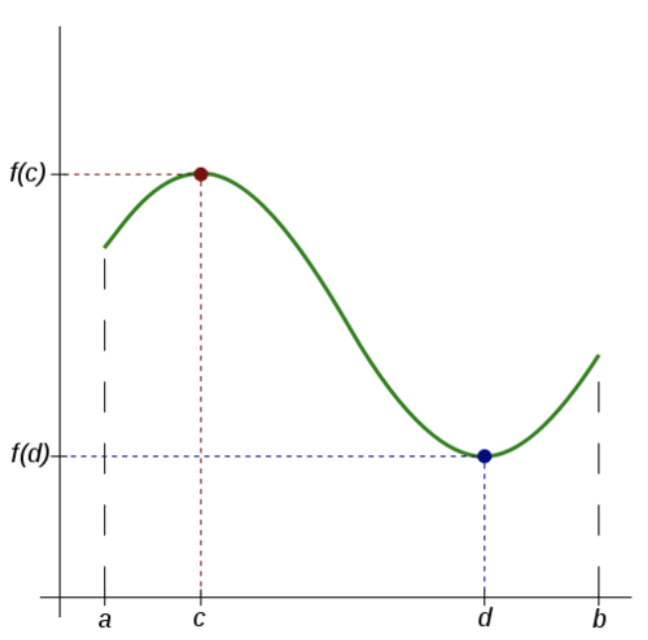
Fundación CK-12 - http://commons.wikimedia.org/wiki/File:Extreme_Value_Theorem.svg; https://commons.wikimedia.org/wiki/File:CentralParkFromAboveCropped.jpg - CC BY-SA
Lo contrario del Teorema del Valor Extremo es : Si hay al menos un máximo y un mínimo en el intervalo cerrado [a, b] entonces la función es continua en [a, b].
Esta afirmación es falsa. Para mostrar que la declaración es falsa, todo lo que necesitas es un contraejemplo. El objetivo es encontrar una función en un intervalo cerrado [a, b] que tenga al menos un máximo y un mínimo y también sea discontinua.
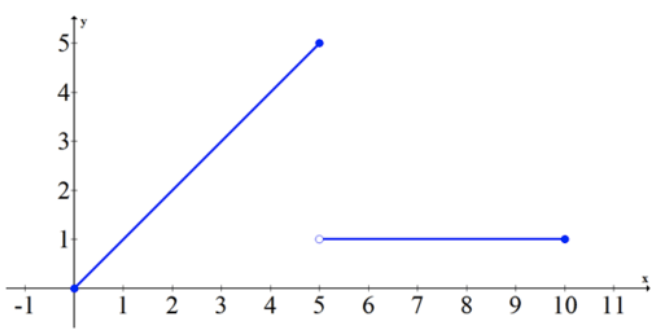
Fundación CK-12 - CC BY-SA
En el intervalo [0,10], la función alcanza un máximo en (5,5) y un mínimo en (0,0) pero sigue siendo discontinua.
Ejemplos
Ejemplo 1
Anteriormente, se le pidió aplicar los Teoremas de Valor Intermedio y Extremo a una función es continua en el intervalo x∈ [1,4]. Se puede concluir por el Teorema del Valor Intermedio que existe un c∈ [1,4] tal que f (c) =u por cada u entre f (1) y f (4). También se puede concluir que en este intervalo la función tiene tanto un valor máximo como un mínimo por el Teorema del Valor Extremo.
Ejemplo 2
Usa el Teorema del Valor Intermedio para mostrar que la función f (x) = (x+1) 3 −4 tiene un cero en el intervalo [0,3].
Primero tenga en cuenta que la función es cúbica y por lo tanto es continua en todas partes.
- f (0) = (0+1) 3 −4=1 3 −4=−3
- f (3) = (3+1) 3 −4=4 3 −4=60
Por el Teorema del Valor Intermedio, debe existir un c∈ [0,3] tal que f (c) =0 ya que 0 está entre -3 y 60.
Ejemplo 3
Utilice el Teorema del Valor Intermedio para mostrar que la siguiente ecuación tiene al menos una solución real.
x 8 =2 x
Primero reescribe la ecuación: x8−2x=0
Luego describirlo como una función continua: f (x) =x8−2x
Esta función es continua porque es la diferencia de dos funciones continuas.
- f (0) =0 8 −2 0 =0−1=−1
- f (2) =2 8 −2 2 =256−4=252
Por el Teorema del Valor Intermedio, debe existir una c tal que f (c) =0 porque −1<0<252. El número c es una solución a la ecuación inicial.
Ejemplo 4
Demostrar que hay al menos una solución a la siguiente ecuación.
sinx=x+2
Escribe la ecuación como una función continua: f (x) =sinx−x−2
La función es continua porque es la suma y diferencia de funciones continuas.
- f (0) =sin0−0−2=−2
- f (−π) =sin (−π) +π−2=0+π−2>0
Por el Teorema del Valor Intermedio, debe existir una c tal que f (c) =0 porque −2<0<π−2. El número c es una solución a la ecuación inicial.
Ejemplo 5
¿Cuándo no se le permite utilizar el Teorema del Valor Intermedio?
El Teorema del Valor Intermedio no debe aplicarse cuando la función no es continua en el intervalo.
Revisar
Utilice el Teorema del Valor Intermedio para mostrar que cada ecuación tiene al menos una solución real.
1. cosx=−x
2. ln (x) =e −x +1
3. 2x 3 −5x 2 =10x−5
4. x 3 +1=x
5. x 2 =cosx
6. x 5 =2x 3 +2
7. 3x 2 +4x−11=0
8. 5x 4 =6x 2 +1
9. 7x 3 −18x 2 −4x+1=0
10. Mostrar que f (x) = 2x−3/2x−5 tiene una raíz real en el intervalo [1,2].
11. Mostrar que f (x) = 3x+1/2x+4 tiene una raíz real en el intervalo [−1,0].
12. Verdadero o falso: Una función tiene un máximo y un mínimo en el intervalo cerrado [a, b]; por lo tanto, la función es continua.
13. Verdadero o falso: Una función es continua a lo largo del intervalo [a, b]; por lo tanto, la función tiene un máximo y un mínimo en el intervalo cerrado.
14. Verdadero o falso: Si una función es continua a lo largo del intervalo [a, b], entonces es posible que la función tenga más de un máximo relativo en el intervalo [a, b].
15. ¿Qué tienen que ver con la continuidad los teoremas de Valor Intermedio y Valor Extremo?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 14.7.
vocabulario
| Término | Definición |
|---|---|
| continuidad | La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido. |
| Continuo | La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido. |
| converse | Si una declaración condicional es p→q (si p, entonces q), entonces lo contrario es q→p (si q, entonces p. Tenga en cuenta que lo contrario de una declaración no es cierto solo porque la declaración original es verdadera. |
| contraejemplo | Un contraejemplo es un ejemplo que desmiente una conjetura. |
| Teorema del valor extremo | El teorema del valor extremo establece que en cada intervalo [a, b] donde una función es continua hay al menos un máximo y un mínimo. Es decir, debe tener al menos dos valores extremos. |
| Teorema del valor intermedio | El teorema del valor intermedio establece que si f (x) es continuo en algún intervalo [a, b] y n está entre f (a) y f (b), entonces hay algo de c∈ [a, b] tal que f (c) =n. |
Recursos adicionales
PLIX: Juega, aprende, interactúa, explora - Exploración de funciones
Video: Regla de Señales de Descartes - Ejemplo 1
Práctica: Teorema del Valor Intermedio, Existencia de Soluciones
Mundo Real: Altas y Bajadas