7.1: Derivadas con Teorema del Valor Medio y Teorema de Rolle
- Page ID
- 105824
Jim le estaba contando a su amigo mayor de matemáticas sobre una multa por exceso de velocidad que había recibido recientemente por superar las 80 mph un fin de semana por la mañana cuando había poco tráfico en la carretera. Al parecer, dos policías en diferentes lugares a lo largo de la carretera lo habían registrado yendo a 60 y 65 mph respectivamente mientras pasaba por cada una de sus posiciones de trampa de velocidad. Jim dijo que sabía dónde estaban ubicadas las trampas de velocidad y siempre se aseguró de que estuviera dentro del límite de velocidad que pasaba, así que no podía entender cómo podían decir que iba a exceso de velocidad. El amigo mayor de matemáticas de Jim preguntó si el oficial que emitió el boleto había dicho algo. Jim recordó que el oficial había mencionado que las trampas de velocidad estaban exactamente a 3 millas de distancia, y que sabían que el auto de Jim había cubierto la distancia en 2 minutos. El amigo mayor de matemáticas de Jim sonrió y dijo: “Oh, así lo hicieron: El teorema del valor medio”. Jim se veía muy perplejo.
¿Puedes averiguar cómo el policía podría haber emitido un boleto sin presenciar realmente el auto de Jim sobrepasando las 80 mph?
El teorema del valor medio
En un concepto anterior, la derivada de una función se introdujo como la pendiente de la línea tangente en un punto. Observamos cómo cambió la pendiente de una línea secante a medida que uno de los dos puntos se acercaba al otro. La línea secante se convirtió en la línea tangente en el límite como se ilustra a continuación.
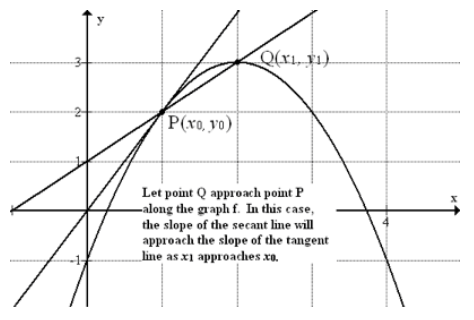
CC BY-NC-SA
Ahora miramos los valores de pendiente de las líneas tangentes en un intervalo definido por la línea secante entre dos puntos. El siguiente teorema da una relación importante.
Teorema de Rolle: Si f es continuo en un intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b), y si f (a) =f (b) entonces f tiene al menos un valor c en el intervalo abierto (a, b) tal que f′ (c) =0.
Veamos si puedes hacer uso del teorema de Rolle
Para la función\( f(x)=x^2−3x−10 \nonumber\), mostrar que satisface las condiciones del teorema de Rolle en el intervalo [-2, 5] y encontrar todos los números c en (-2, 5) que satisfagan f′ (c) =0
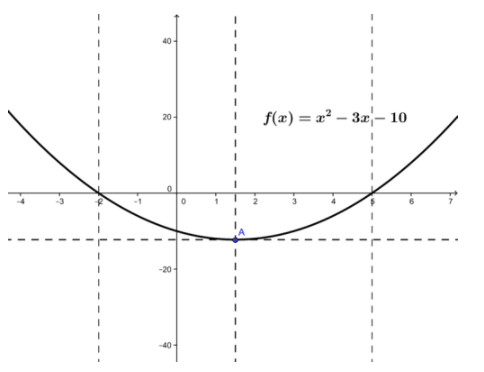
CC BY-NC-SA
Evaluando f (x) a x=−2 y x=5 rinde:
\[ f(−2)=(−2)^2−3(−2)−10 \nonumber\]
\[ =0 \nonumber\]
\[ f(5)=(5)^2−3(5)−10 \nonumber\]
\[ =0 \nonumber\]
Por lo tanto f (−2) =f (5), que satisface las condiciones para que el teorema de Rolle se mantenga.
Ahora para encontrar valores de c que satisfagan f′ (c) =0.
\[ \frac{dy}{dx} =2x−3 \nonumber\]
\[ f′(c)=0 \nonumber\]
\[ =2(c)−3 \nonumber\]
\[ ∴c= \frac{3}{2} \nonumber\]
Así\( f′( \frac{3}{2})=0 \nonumber\) satisface el teorema de Rolle.
Considera la función\( f(x)=x^{ \frac{2}{3}} \nonumber\). En el intervalo [-4, 4], f (−4) =f (4). No obstante, ¿hay algún punto en el que la derivada de\( f(x)=x^{ \frac{2}{3}} \nonumber\) sea igual a cero? ¿Es esto una contradicción del teorema de Rolle?
La curva de función para\( f(x)=x^{ \frac{2}{3}} \nonumber\) se muestra a continuación.
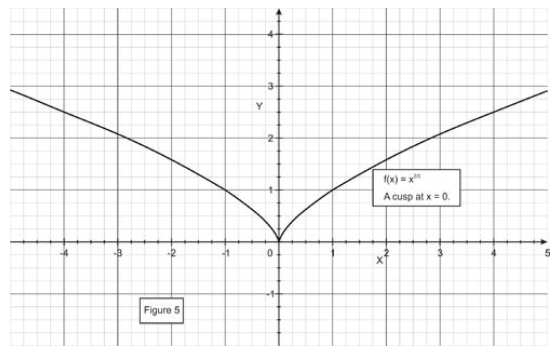
CC BY-NC-SA
Es derivado is\( f′(x)= \frac{2}{3x^{ \frac{1}{3}}} \nonumber\), que está indefinido en x=0, y no hay ningún punto en el que la derivada sea 0. Pero, debido a que la función no es diferenciable a lo largo del intervalo, el teorema de Rolle no se aplica. No hay contradicción.
El teorema de Rolle requiere que f (a) =f (b). Pero el teorema de Rolle es la base para probar el importante teorema general llamado Teorema del Valor Medio que no requiere f (a) =f (b).
Teorema del Valor Medio: Si f es una función continua en un intervalo cerrado [a, b] y si f′ contiene el intervalo abierto (a, b) en su dominio, entonces existe un número c en el intervalo (a, b) tal que
\[ f′(c)= \frac{f(b)−f(a)}{b−a} \nonumber\]
Una forma equivalente es:\( f(b)−f(a)=(b−a)f′(c) \nonumber\).
En la siguiente figura se muestra una ilustración del significado del Teorema del Valor Medio, donde se puede encontrar que la pendiente de la línea secante que conecta f (a) y f (b) es la misma que la pendiente de la línea tangente en f (c).
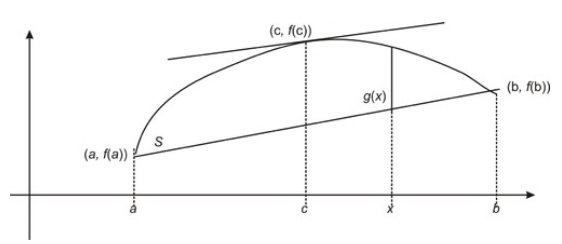
CC BY-NC-SA
Verificar que el Teorema del Valor Medio aplique para la función\( f(x)=x^3+3x^2−24x \nonumber\) en el intervalo [1, 4].
Necesitamos encontrar c en el intervalo (1, 4) tal que\( f′(c)= \frac{f(4)−f(1)}{(4−1)} \nonumber\)
\[ f′(c)= \frac{f(4)−f(1)}{(4−1)} \nonumber\]
\[ =16+203 \nonumber\]
\[ =12 \nonumber\]
Tenga en cuenta que
\[ f′(x)=3x^2+6x−24 \nonumber\]
De ahí que debemos resolver la siguiente ecuación:
\[ 3c^2+6c−24=12 \nonumber\]
\[ 3c^2+6c−32=0 \nonumber\]
\[ c^2+2c−12=0 \nonumber\]
\[ c=−1± \sqrt{13} \nonumber\]
Como necesitamos tener c en el intervalo (1, 4), la raíz positiva es la solución:
c≈2.61.
Ejemplos
Ejemplo 1
Anteriormente, te preguntaron sobre cómo Jim podría obtener una multa por exceso de velocidad por ir al menos a 80 mph cuando la velocidad de su automóvil se registró en 60 mph y 65 mph.
La información clave fue que el policía determinó que Jim había viajado 3 millas en 2 minutos, por lo que la velocidad promedio de Jim era de 90 mph. El gran amigo de Jim en matemáticas sabía que según el Teorema del Valor Medio tenía que haber habido al menos una vez en que la velocidad real de Jim era de 90 mph, definitivamente superando las 80 mph.
Ejemplo 2
Verifique que el Teorema del Valor Medio aplique para la función\( f(x)=2sinx+3cosx \nonumber\) en el intervalo\( (0,2π) \nonumber\).
Necesitamos encontrar c en el intervalo (0,2π) de tal manera que\( f′(c)= \frac{f(2π)−f(0)}{(2π−0)} \nonumber\):
\[ f′(c)= \frac{f(2π)−f(0)}{(2π−0)} \nonumber\]
\[ = \frac{2−2}{2π} \nonumber\]
\[ =0 \nonumber\]
Tenga en cuenta que
\[ f′(x)=2cosx−3sinx \nonumber\]
De ahí que debemos resolver la siguiente ecuación:
\[ 2cosc−3sinc=0 \nonumber\]
\[ tanc= \frac{2}{3} \nonumber\]
\[ c=tan^{−1} ( \frac{2}{3}) \nonumber\]
\( c=0.588 \nonumber\)radianes... y también\( (0.588+π) \nonumber\) radianes en el intervalo\( (0,2π) \nonumber\).
El Teorema del Valor Medio se aplica en dos lugares del intervalo\( (0,2π) \nonumber\).
Revisar
Para #1 -5, si es posible, verificar el Teorema de Rolle para las siguientes funciones encontrando valores de x para los cuales f (x) =0 y f′ (x) =0. Si no es posible, exponer por qué.
- \( f(x)=3x^3−12x \nonumber\)
- \( f(x)=x^2−2x−1 \nonumber\)
- \( f(x)=−2x^2−12x+5 \nonumber\)
- \( f(x)=|2x−3| \nonumber\)
- \( f(x)=2sinx+3cosx \nonumber\)
- \( f(x)=x^4−2x^2 \nonumber\)
- Demostrar que si la ecuación\( x^3+a_1x^2+a_2x=0 \nonumber\) tiene una raíz positiva en x=r y que la ecuación\( 3x^2+2a_1x+a_2=0 \nonumber\) tiene una raíz positiva menor que r.
Para #8 -15, verifique que el Teorema del Valor Medio funcione para cada función en el intervalo especificado, o indique por qué no.
- \( f(x)=(x+2)x, [1, 2] \nonumber\)
- \( f(x)=2x, [-1,1] \nonumber\)
- \( f(x)=x^2−5x+1, [0, 3] \nonumber\)
- \( f(x)=5−4x, [1, 4] \nonumber\)
- \( f(x)=x^3−8x−5, [1, 4] \nonumber\)
- \( f(x)=sinx, [0, \frac{π}{2}] \nonumber\)
- \( f(x)=cosx, [0, \frac{π}{2}] \nonumber\)
- \( f(x)=2x, [0, 3] \nonumber\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.3.
El vocabulario
| Término | Definición |
|---|---|
| Teorema del valor medio | El teorema del valor medio para integrales definidas establece que si f es continuo en el intervalo cerrado [a, b] entonces en algún punto c en el intervalo abierto (a, b):\( \int\limits_{a}^{b} f(x)dx=f(c)(b−a) \nonumber\) |
| Teorema de Rolle | El teorema de Rolle dice que una función que tiene el mismo valor en dos puntos tiene una derivada de 0 al menos un punto en el intervalo |
Recursos adicionales
PLIX: Jugar, Aprender, Interactuar, Explorar - Máximas y Mínimas, Teorema del Valor Medio, Teorema de Rolle
Video: Teorema del Valor Medio
Práctica: Derivadas con Teorema del Valor Medio y Teorema de Rolle
Mundo real: Dignando

