7.2: Absoluto versus Extrema Local
- Page ID
- 105836
Ser capaz de identificar los valores más pequeños y mayores de una función (extrema), y donde ocurren en algún intervalo en el dominio o en todo el dominio, es útil para graficar una ecuación de función así como para resolver problemas de “optimización”. La ubicación de estos extremos está ligada al comportamiento de la derivada. Aprendiste en trabajos previos con funciones cuadráticas (parábolas,\( y=ax^2+bx+c \nonumber\)), que el menor o mayor valor de la parábola se podía encontrar en el vértice de la parábola (en el eje de simetría\( x=− \frac{b}{2a} \nonumber\)). ¿Cómo se\( x=− \frac{b}{2a} \nonumber\) relacionan la derivada de la función cuadrática y el vértice?
Extrema
Comencemos nuestra discusión con algunas definiciones formales de trabajo de los valores máximos y mínimos de una función.
- Una función f tiene un máximo en x=a si\( f(a)≥f(x) \nonumber\) para todos x en el dominio de f.
- Una función f tiene un mínimo en x=a si\( f(a)≤f(x) \nonumber\) para todos x en el dominio de f.
Los valores de la función para estos valores x se denominan valores extremos o extremos.
Aquí hay un ejemplo de una función que tiene un máximo en x=a y un mínimo en x=d:
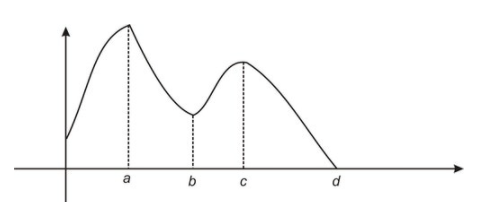
CC BY-NC-SA
Observe la gráfica en x=b. Si bien no tenemos un mínimo en x=b, observamos que f (b) ≤f (x) para todos x cerca de b. Decimos que la función tiene un mínimo local en x=b.
De igual manera, decimos que la función tiene un máximo local en x=c ya que f (c) ≥f (x) para algunos x contenidos en intervalos abiertos de c.
Recuerda usar los términos máximo y mínimo (sin incluir el término local) solo cuando estés hablando de los valores extremos absolutos o globales de la función; los extremos locales o extremos relativos deben llamarse máximo local o mínimo local.
¿Todas las funciones tienen un máximo y mínimo? Sí, todas las funciones continuas lo hacen. Esto lo afirma el Teorema del Valor Extremo que discutimos en el concepto de Continuidad.
Teorema de Valor Extremo: Si una función f (x) es continua en un intervalo cerrado I, entonces f (x) tiene tanto un valor máximo como un valor mínimo en I.
Esto tiene sentido conceptualmente. Intente dibujar una función (en un intervalo cerrado, incluidos los puntos finales) para que ningún punto esté en la parte más alta de la gráfica. No importa cómo se esboce la función, habrá al menos un punto que sea el más alto.
¿Cómo se relacionan los valores extremos, máximos y mínimos, con los derivados? El matemático francés Fermat muestra cómo en el Teorema de Fermat: Si f (c) es un valor extremo de f para algún intervalo abierto que contiene c, entonces f′ (c) =0, o f′ (c) no existe.
Esta relación entre la ubicación de los extremos y la derivada en la ubicación es tan importante que le damos a la ubicación el nombre punto crítico.
Llamaremos a x=c un punto crítico en el intervalo cerrado [a, b] si f (c) existe, y ya sea f′ (c) =0 o f′ (c) no existe.
Resumen hasta ahora: Si una función es continua en un intervalo cerrado, tiene tanto un mínimo como un máximo en alguna ubicación (es), y la derivada en estas ubicaciones es 0 o no existe. Las ubicaciones se denominan puntos críticos.
El siguiente diagrama identifica explícitamente cómo identificar los puntos críticos. Los puntos finales del intervalo cerrado se incluyen como puntos críticos si consideramos la función solo definida en el intervalo cerrado y no fuera del intervalo. En este caso, no se definiría la derivada en cada punto final.
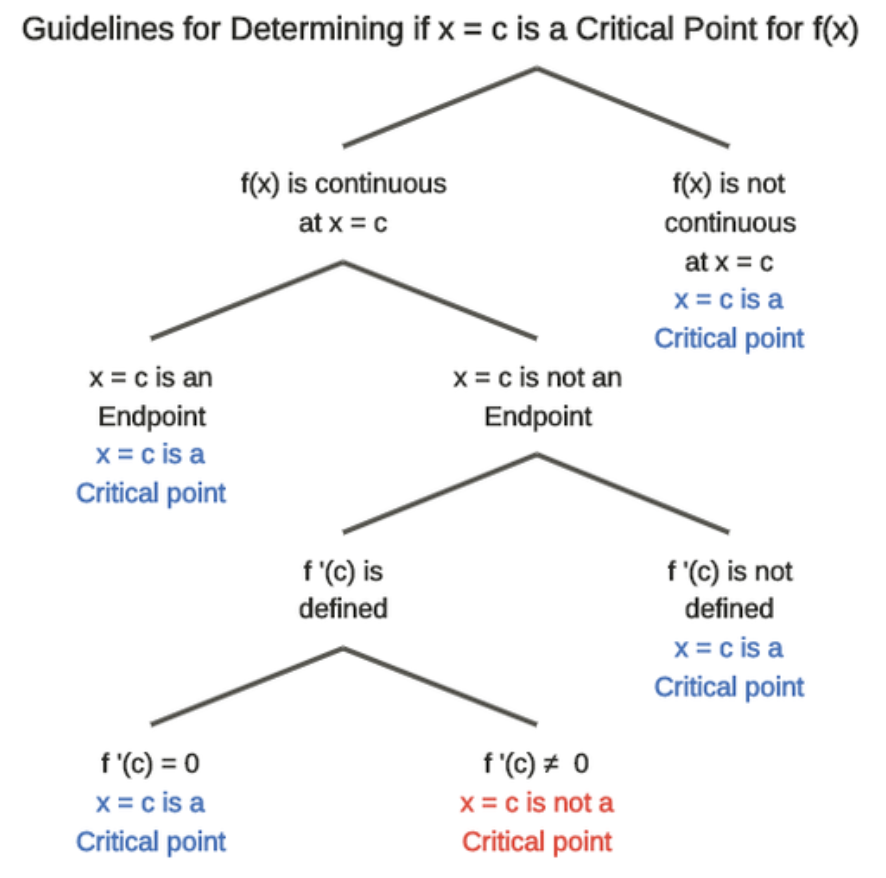
Un diagrama de árbol para ayudar a identificar puntos críticos. Fundación CK-12
Consideremos las dos funciones que se muestran a continuación y digamos algo sobre ellas en el intervalo cerrado [-2, 2]. Observe que g (x) (la segunda función) tiene una cúspide en x=0.
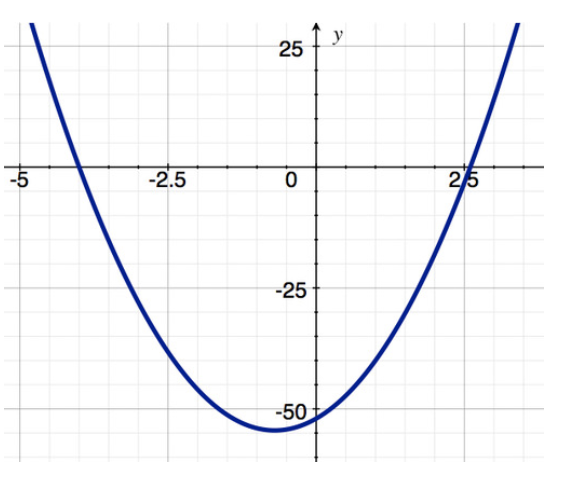
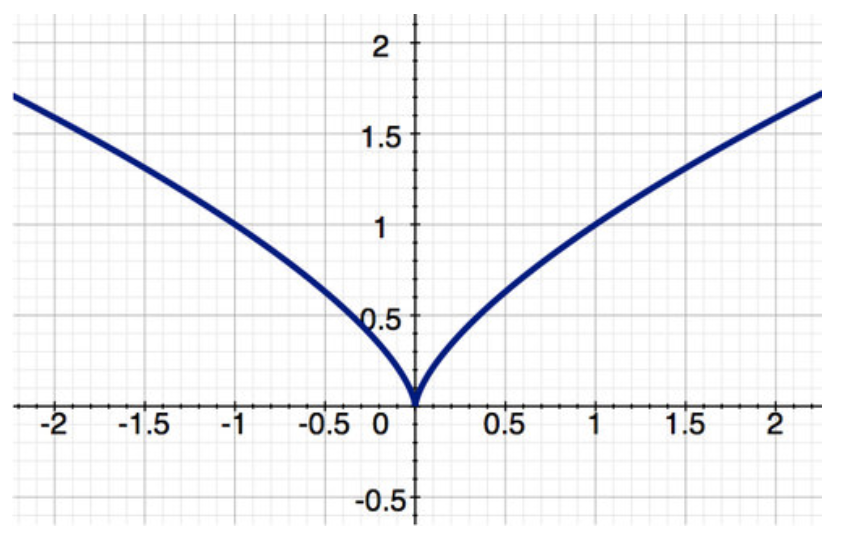
Dos funciones
Ambas funciones son continuas en [-2, 2]. Por el Teorema del Valor Extremo ambos tienen un mínimo y un máximo. Como muestra la tabla, f (x) tiene un valor extremo donde f′ (x) =0, y g (x) tiene un valor extremo donde g′ (x) no está definido. Estos son puntos críticos.
| Propiedad Function | \( f(x)=5x^2+7x−52 \nonumber\) | \( g(x)=x^{\frac{2}{3}} \nonumber\) |
| Valor en el punto final x=−2 | -46 | 1.59 |
| Valor en el punto final x=2 | -18 | 1.59 |
| Ubicación y valor donde f′ (x) =0 | (-0.7, -54.45) | — |
| Ubicación donde no existe f′ (x) | Puntos finales | Puntos finales, x=0 |
| Punto (s) crítico (s) | x=−0.7 Puntos finales | x=0, Puntos finales |
| Valor mínimo y ubicación (es) | (-0.7, -54.45) | (0, 0) |
| Ubicación (es) de Valor máximo | (2, -18) | (-2, 1.59) (2, 1.59) |
Cabe señalar que lo contrario del Teorema del Valor Extremo no es necesariamente cierto, es decir, solo porque f′ (x) =0 en alguna ubicación x=a, el valor de la función f (a) no tiene que ser un mínimo o máximo local.
Considerar\( f(x)=x^3 \nonumber\) y su gráfica. Vemos que mientras f′ (0) =0 en x=0, x=0 no es un punto extremo de la función.
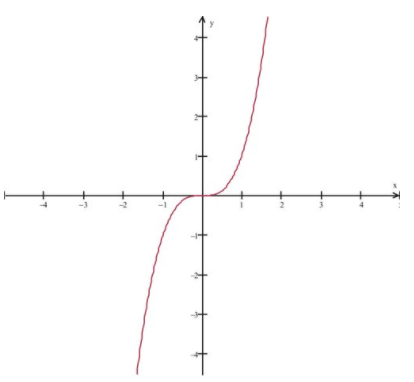
CC BY-NC-SA
Ejemplos
Ejemplo 1
Anteriormente, se le pidió que determinara cómo se relacionan la derivada de la función cuadrática\( (y=ax^2+bx+c) \nonumber\) y la fórmula\( x=− \frac{b}{2a} \nonumber\) del vértice.
Si te diste cuenta de que el vértice de la función cuadrática es también la ubicación donde la pendiente de la línea tangente, y por lo tanto la derivada, es igual a 0 hiciste una gran observación. \( \frac{dy}{dx}=2ax+b=0 \nonumber\)significa eso\( x=− \frac{b}{2a} \nonumber\). Este es el valor x del vértice, y un valor crítico o punto de la función.
Ejemplo 2
La función\( f(x)= \sqrt{25−x^2} \nonumber\) es la parte superior de un círculo centrado en (0, 0) con radio 5. Encuentra los puntos críticos de la función, y los máximos y mínimos.
Calcula la derivada:\( f′(x) = \frac{1}{2 \sqrt{25−x^2}}(−2x) = − \frac{x}{ \sqrt{25−x^2}} \nonumber\)
f′ (x) =0 significa x=0 es un punto crítico, y f (0) =5.
Observe que f′ (x) no está definido en las dos ubicaciones x=±5, lo que significa que estos son puntos críticos. Ambos valores están asociados con valores de función f (±5) =0.
Los mínimos de la función están en (-5, 0) y (5, 0); el máximo de la función está en (0, 5).
Revisar
Para #1 -3, identifica los valores mínimos y máximos absolutos y locales de la función (si existen); encuentra los extremos. (Unidades en los ejes indican1 unidad).
- Continuo en [0, 9]
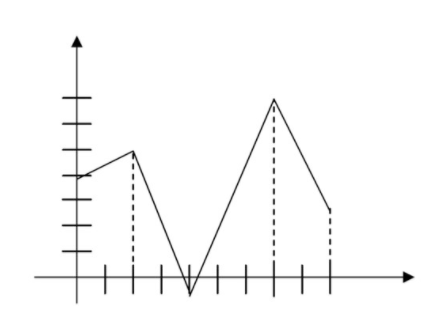
CC BY-NC-SA
- Continuo en [0, 9]
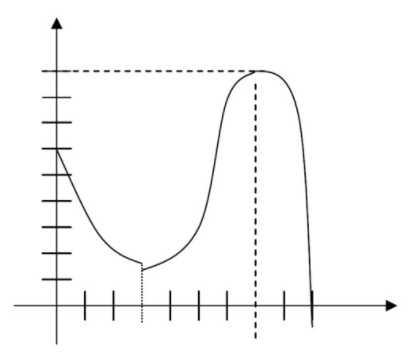
CC BY-NC-SA
- Continuo en [0,4] [4,9]
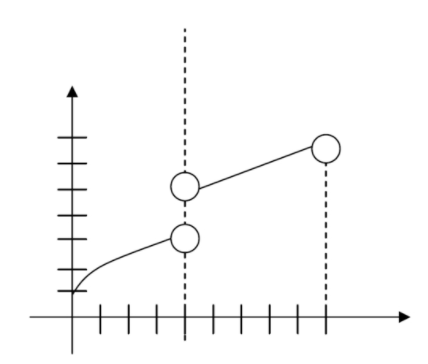
CC BY-NC-SA
Para #4 —6, encuentra los extremos y dibuja la gráfica.
- \( f(x)=−x^2−6x+4, [-4, 1] \nonumber\)
- \( f(x)=x^3−x^4, [0, 2] \nonumber\)
- \( f(x)=−x^2+4x^2, [-2, 0] \nonumber\)
- ¿Cuál es el máximo absoluto de la función sinusoidal en el intervalo\( [0,π] \nonumber\)?
- ¿Cuáles son los mínimos locales de la función coseno a lo largo del intervalo\( [0,2π] \nonumber\)?
- ¿Cuál es el máximo absoluto y el mínimo absoluto de la función\( x^2 \nonumber\) a lo largo del intervalo [6, 7]?
- ¿En qué momento la función\( f(x)=(x^2−7x−8)^4 \nonumber\) alcanza su mínimo absoluto a lo largo del intervalo [5, 10]?
- Sea [a, b] un intervalo cerrado y finito, y deje que f (x) sea una línea recta. Si f (x) alcanza su valor máximo sobre [a, b] en puntos distintos a a y b, ¿qué debe ser cierto acerca de f (x)?
- Encuentra todos los números críticos de\( f(x)=3x^4− \frac{8}{3}x^3−6x^2+8x+1 \nonumber\).
- Encuentra todos los números críticos de\( f(x)=\frac{1}{2x^2−5x−3} \nonumber\).
- Encuentra todos los números críticos de\( f(x)=ln(x−4) \nonumber\).
- Encuentra todos los números críticos de\( f(x)=\sqrt{x} ×(1−x) \nonumber\).
- Encuentra todos los números críticos de\( f(x)= \frac{x^2+x+1}{x−2} \nonumber\).
- ¿El polinomio\( f(x)=x^6+x^4+x^2+1 \nonumber\) alcanza un valor mínimo a lo largo del intervalo\( [−π,π] \nonumber\)?
- ¿La función\( f(x)=7^{sin(x)} \nonumber\) alcanza un valor máximo a lo largo del intervalo\( (0,π) ] \nonumber\)?
- ¿La función\( f(x)= \frac{10}{x} \nonumber\) alcanza un valor máximo en el intervalo [-1, 1]?
- ¿La función\( f(x)=sin( \frac{x}{2}) \nonumber\) alcanza un valor mínimo a lo largo del intervalo\( (0,π) \nonumber\)?
- Sea a y b dos números positivos tal que a<b. ¿La función f (x) =ln (x) alcanza un valor máximo en el intervalo [a, b]?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.2.
El vocabulario
| Término | Definición |
|---|---|
| punto crítico | Un valor crítico (o punto) es un valor en un intervalo cerrado del dominio de la función donde o bien la derivada de función en el punto es 0, o la derivada no existe. |
| derivado | La derivada de una función es la pendiente de la línea tangente a la función en un punto dado de la gráfica. Las notaciones para derivados incluyen f′ (x)\( \frac{dy}{dx} \nonumber\),, y′\( \frac{df}{dx} \nonumber\) y\ frac {df (x)} {dx}. |
| Extrema | Extrema es un término colectivo que abarca tanto los valores mínimos como los máximos, refiriéndose a los valores “extremos” de la función. |
| extrema global | Los extremos globales de una función son los puntos con los valores y que son los más altos o los más bajos de toda la función. |
| Máximo Global | El máximo global de una función es el valor más grande de toda la función. Simbólicamente, es el punto más alto de toda la gráfica. |
| Mínimo Global | El mínimo global de una función es el valor más pequeño de toda la función. Simbólicamente, es el punto más bajo de toda la gráfica. |
| extrema local | Los extremos locales de una función son los puntos de la función con valores y que son los más altos o más bajos de un vecindario local de la función. |
| Máximo Local | Un máximo local es el punto más alto relativo a los puntos que lo rodean. Una función puede tener más de un máximo local. |
| Mínimo Local | Un mínimo local es el punto más bajo relativo a los puntos que lo rodean. Una función puede tener más de un mínimo local. |
| Máximo | El máximo es el punto más alto de una gráfica. El máximo arrojará el mayor valor del rango. |
| Mínimo | El mínimo es el punto más bajo de una gráfica. El mínimo arrojará el valor más pequeño del rango. |
Recursos adicionales
PLIX: Jugar, Aprender, Interactuar, Explorar - Absoluto versus Extrema Local
Video: L ocal y Máximo y Mínimo Absoluto
Práctica: Absoluto versus Extrema Local

