7.3: Prueba de Primera Derivada
- Page ID
- 105814
Si observa alguna curva de función, puede determinar visualmente si la función está aumentando, disminuyendo o permaneciendo constante durante un intervalo. También se puede ver aproximadamente donde la función alcanza puntos altos y puntos bajos. Hay una manera de determinar matemáticamente, utilizando la derivada, lo que proporcionan tus observaciones visuales. ¿Cómo te ayuda conocer la pendiente de una línea tangente a calcular con precisión lo que tus observaciones visuales solo pueden estimar?
La Primera Prueba Derivada
Considera las gráficas de las dos funciones a continuación.
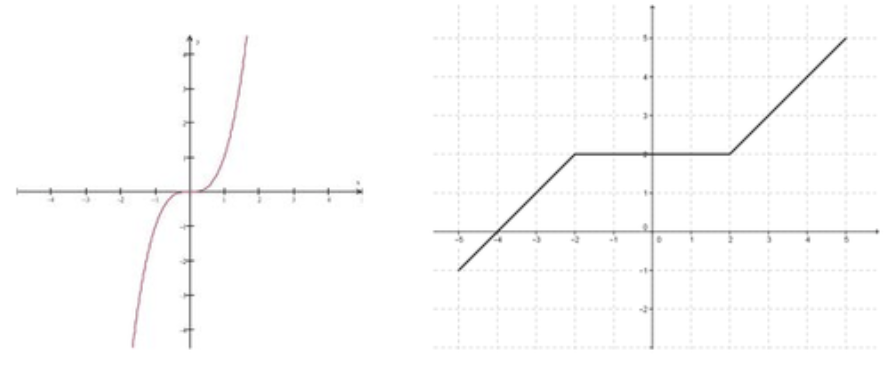
CC BY-NC-SA
Ambas funciones son continuas a lo largo de los intervalos mostrados. En la primera,\( f(x)=x^3 \nonumber\), los valores de la función siempre van aumentando a medida que x aumenta. En el segundo, los valores de la función por partes aumentan a lo largo del intervalo [-5, -2], permanecen iguales durante el intervalo [-2, 2], luego vuelven a aumentar para [2, 5].
La diferencia entre estos dos casos de aumento de los valores de función motiva la necesidad de las siguientes distinciones:
- Se dice que una función f está aumentando en [a, b] contenida en el dominio de f si\( f(x_1)≤f(x_2) \nonumber\) siempre\( x_1≤x_2 \nonumber\) para todos\( x_1,x_2∈[a,b] \nonumber\).
- Si\( f(x_1)<f(x_2) \nonumber\) siempre\( x_1<x_2 \nonumber\) para todos\( x_1,x_2∈[a,b] \nonumber\), entonces decimos que f está aumentando estrictamente en [a, b].
De manera similar:
- Se dice que una función f está disminuyendo en [a, b] contenida en el dominio de f si\( f(x_1)≤f(x_2) \nonumber\) siempre\( x_1≥x_2 \nonumber\) para todos\( x_1,x_2∈[a,b] \nonumber\).
- Si\( f(x_1)>f(x_2) \nonumber\) siempre\( x_1>x_2 \nonumber\) para todos\( x_1,x_2∈[a,b] \nonumber\). Entonces decimos que f es estrictamente decreciente en [a, b].
Tenga en cuenta que los símbolos\( ϵ \nonumber\) y\( ∈ \nonumber\) son equivalentes y denotan que un elemento en particular está contenido dentro de un conjunto particular.
Usando la terminología anterior, decimos que la función\( f(x)=x^3 \nonumber\) está aumentando estrictamente a lo largo del intervalo dado, y la función por partes está aumentando a lo largo del intervalo.
Ahora mira las derivadas de las dos funciones graficadas arriba.
Ahora podemos afirmar un teorema que relaciona la derivada de una función con las propiedades de aumento/disminución de la función.
Si f es continuo en el intervalo [a, b], y diferenciable en (a, b) entonces:
- Si f′ (x) >0 para cada\( x∈(a,b) \nonumber\), entonces f está aumentando en [a, b].
- Si f′ (x) <0 para cada\( x∈(a,b) \nonumber\), entonces f está disminuyendo en [a, b].
Toma la función\( f(x)=x^3−3x^2−6x+8 \nonumber\). Para encontrar los intervalos en los que f está aumentando y los intervalos en los que f está disminuyendo, primero tenga en cuenta que la función f (x) es continua en todas partes. La derivada de la función es\( f′(x)=3x^2−6x−6=3(x^2−2x−2) \nonumber\), que es una parábola con dos intercepciones x (números críticos de f) at\( x=1±\sqrt{3} \nonumber\). La evaluación de f′ (x) en los tres intervalos que son definidos por las dos raíces proporciona la siguiente información:
\[ f'(x) = \begin{cases} >0, & x<1- \sqrt{3} & f(x) \mbox{ is increasing} \\ =0, & x = 1 - \sqrt{3} \\ <0 & (1- \sqrt{3})<x<(1+ \sqrt{3}) & f(x) \mbox{ is decreasing} \\ =0, & x = 1 + \sqrt{3} \\ >0, & x>1+ \sqrt{3} & f(x) \mbox{ is increasing} \end{cases} \nonumber\]
Los cambios en la derivada de una función de positivo a negativo, o de negativo a positivo pueden indicar la presencia de un extremo local.
La Prueba de Primera Derivada describe dónde están estos extremos y qué tipo son. La Prueba de Primera Derivada es la siguiente:
Supongamos que f es una función continua y que x=c es un valor crítico de f, entonces:
- Si f′ cambia de positivo a negativo en x=c, entonces f tiene un máximo local en x=c.
- Si f′ cambia de negativo a positivo en x=c, entonces f tiene un mínimo local en x=c.
- Si f′ no cambia de signo en x=c, entonces f no tiene ni un máximo local ni mínimo en x=c.
Podemos observar las consecuencias de este teorema observando las líneas tangentes de la siguiente gráfica en cada uno de los intervalos (0, a), (a, b), (b, +∞).
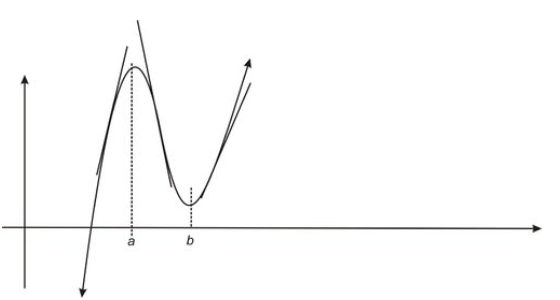
CC BY-NC-SA
Observe primero que tenemos un máximo relativo en x=a y un mínimo relativo en x=b Las pendientes de las líneas tangentes cambian de positivo para x∈ (0, a) a negativo para x∈ (a, b) y luego de vuelta a positivo para x∈ (b, +∞).
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó cómo se relaciona la pendiente de la línea tangente con si una función está aumentando o disminuyendo o no. Pendiente positiva significa una función creciente; pendiente negativa significa una función decreciente. A menudo, la transición de pendiente de positivo (negativo) a negativo (positivo) indica la ubicación de un extremo.
Ejemplo 2
Considera la gráfica de funciones a continuación. Determinar si la función donde la función es estrictamente creciente o decreciente.
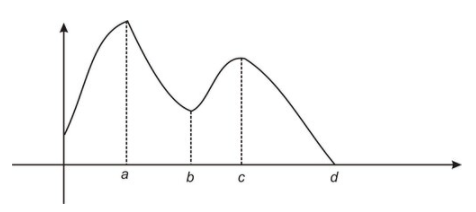
CC BY-NC-SA
La función aquí indicada es estrictamente creciente en (0, a) y (b, c), y estrictamente decreciente en (a, b) y (c, d).
Ejemplo 3
Consideremos la función\( f(x)=x^2+6x−9 \nonumber\) y observemos la gráfica alrededor de x=−3. ¿Qué sucede con la primera derivada cercana a este valor?
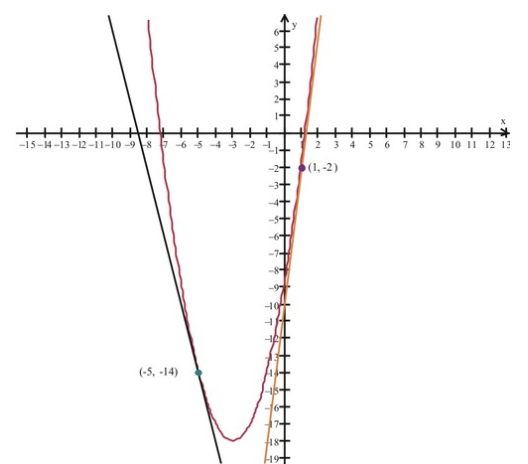
CC BY-NC-SA
Con\( f(x)=x^2+6x−9 \nonumber\), la derivada es\( f′(x)=2x+6 \nonumber\). Observe que la siguiente condición se aplica a las pendientes de las líneas tangentes:
\[ f'(x) \begin{cases} <0, & x < -3 \\ =0, & x = 0 \\ >0, & x > -3 \end{cases} \nonumber\]
Observamos que las pendientes de las líneas tangentes a la gráfica cambian de negativo a positivo en x=−3. La primera prueba derivada establece que f (x) tiene un mínimo local en x=−3. El gráfico de funciones lo verifica.
Revisar
Para #1 -2, identifique los intervalos donde la función está aumentando, disminuyendo o es constante. (Las unidades en los ejes indican unidades individuales).
1. 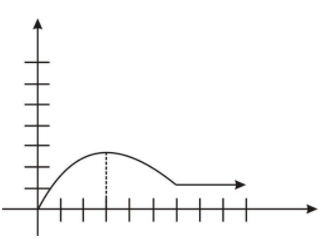
figura5
2. 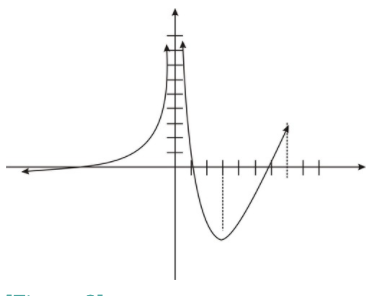
figura6
3. Dar la señal de las siguientes cantidades para la gráfica en el problema 2.
- f′ (−3)
- f′ (1)
- f′ (3)
- f′ (4)
Para #4 -6, determine los intervalos en los que la función está aumentando y aquellos en los que está disminuyendo, luego dibuje la gráfica de cada función.
- \( f(x)=x^2−\frac{1}{x} \nonumber\)
- \( f(x)= (x^2−1)^5 \nonumber\)
- \( f(x)=(x^2−1)^4 \nonumber\)
Para #7 -10:
- Utilice la Prueba de Primera Derivada para encontrar los intervalos en los que la función aumenta y/o disminuye
- Identificar todos los valores máximo, mínimo o relativo máximo y mínimo
- Esbozar la gráfica
- \( f(x)=−x^2−4x−1 \nonumber\)
- \( f(x)=x^3+3x^2−9x+1 \nonumber\)
- \( f(x)=x^{ \frac{2}{3}}(x−5) \nonumber\)
- \( f(x)=2x \sqrt{x2+1} \nonumber\)
- Utilice la prueba de la primera derivada para clasificar los números críticos\( x=0 \nonumber\) y\( x= \frac{3π}{2} \nonumber\) de\( f(x)=cos^2(x) \nonumber\) como máximos o mínimos locales.
- Encuentre los números críticos de\( f(x)=x^5−20x−2 \nonumber\) y clasifíquelos como máximos locales, mínimos o ninguno.
- Encuentra los extremos locales de\( f(x)=x+sin(x) \nonumber\) en el intervalo\( (−2π,2π) \nonumber\).
- Encuentra los extremos globales y locales de\( f(x)=\frac{3}{4}x^4+4x^3−6x^2−48x−50 \nonumber\).
- Encuentra los extremos globales y locales de\( f(x)= \frac{x^2−x−6}{x^2+x−6} \nonumber\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.4.
El vocabulario
| Término | Definición |
|---|---|
| función decreciente | Una función decreciente es aquella con una gráfica que baja de izquierda a derecha. |
| prueba de primera derivada | La primera prueba derivada dice que si f es una función continua y que x=c es un valor crítico de f, entonces si f′ cambia de positivo a negativo en x=c entonces f tiene un máximo local en x=c, si f′ cambia de negativo a positivo en x=c entonces f tiene un mínimo local en x=c, y si f′ no cambia signo en x=c entonces f no tiene ni un máximo local ni mínimo a x=c. |
| aumentar la función | Una función creciente es aquella con una gráfica que sube de izquierda a derecha. |
| estrictamente | Estrictamente es un adjetivo que altera aumentando y disminuyendo para excluir cualquier planitud o periodos donde los valores y se mantengan constantes. |

