7.5: Concavidad e Inflexión

Cuando se definen en un punto, la primera derivada y la segunda derivada proporcionan cada una uno de tres resultados: + (valor > 0), - (valor < 0) o 0. ¿Cuáles son todas las posibilidades de resultado para f′ y f′′, y que dan información definitiva sobre los extremos de f?

---

Aplicación de las Pruebas Derivadas

Ahora aplicaremos todo lo que hemos aprendido de las Pruebas Derivadas Primera y Segunda para bosquejar gráficas de funciones. La siguiente tabla proporciona un resumen de las pruebas y puede ser una guía útil en el bosquejo de gráficos.

Signos de ^1ª y ^2ª Derivadas	Conclusión	Forma de las gráficas
f′ (x) >0 + f′′ (x) >0 +	f está aumentando f es cóncavo hacia arriba	CC BY-NC-SA
f′ (x) >0 + f′′ (x) <0 −	f está aumentando f es cóncavo hacia abajo	CC BY-NC-SA
f′ (x) <0 − f′′ (x) >0 +	f está disminuyendo f es cóncavo hacia arriba	CC BY-NC-SA
f′ (x) <0 − f′′ (x) <0 −	f está disminuyendo f es cóncavo hacia abajo	CC BY-NC-SA

Echa un vistazo a un ejemplo donde podemos usar tanto las Pruebas de Primera como la Segunda Derivada para conocer información que nos permita esbozar la gráfica.

Examinemos la función\( f(x)=x^5−5x+2 \nonumber\).

1. Encuentra los valores críticos para los cuales f′ (c) =0.

\( f′(x)=5x^4−5=0 \nonumber\), que significa\( x^4−1=0 \nonumber\) en x=±1.

2. Aplicar las Pruebas de Primera y Segunda Derivada para determinar los extremos y puntos de inflexión.

Observamos los signos de f′ y f′′ en los intervalos particionados por x=±1,0.

Intervalos clave	f′ (x)	f′′ (x)	Forma de la gráfica
x<−1	+	−	Creciente, cóncava hacia abajo
−1<x<0	−	−	Disminución, cóncava abajo
0<x<1	−	+	Disminución, cóncava arriba
x>1	+	+	Aumento, cóncavo hacia arriba

En los puntos críticos:

1. f′′ (−1) =−20<0. Por la Prueba de Segunda Derivada tenemos un máximo relativo en x=−1, o el punto (-1, 6).
2. f′′ (0) =0. Por la Prueba de Segunda Derivada debemos tener un punto de inflexión debido a la transición de cóncavo hacia abajo a cóncavo hacia arriba entre los intervalos clave.
3. f′′ (1) =20>0. Por la Prueba de Segunda Derivada tenemos un mínimo relativo en x=1, o el punto (1, -2).

Ahora podemos bosquejar la gráfica.

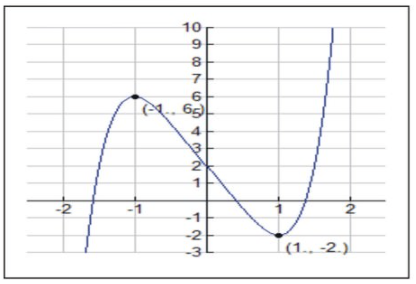
CC BY-NC-SA

Ahora, miren una simple función racional.

Considera la función f (x) =x+2x−3.

1. Encuentra los valores críticos para los cuales f′ (c) =0.

\( f′(x)= \frac{1}{x−3}+(x+2) \frac{−1}{(x−3)^2}= \frac{−5}{(x−3)^2} \nonumber\)lo que significa que no hay valores c que hagan f′ (c) =0.

Dado que f′ (x) no se define en x=3, este es el punto crítico.

2. Observamos los signos de f′ y f′′ en los intervalos particionados por x=3.

Intervalos clave	f′ (x)	f′′ (x)	Forma de la gráfica
x<3	−	−	Disminución, cóncava abajo
x>3	−	+	Disminución, cóncava arriba

En el punto crítico, hay una asíntota vertical y la función y las derivadas son indefinidas; no hay mínimos ni máximos.

Ahora podemos bosquejar la gráfica.

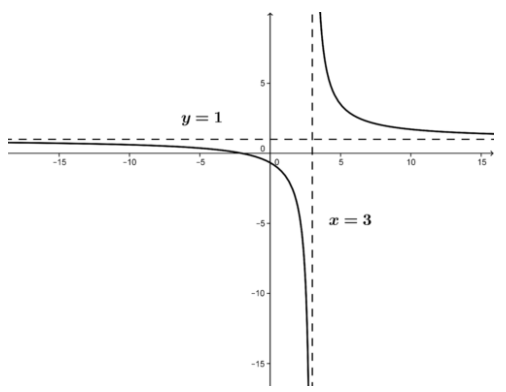
CC BY-NC-SA

---

Ejemplos

Ejemplo 1

Anteriormente, se le pidió que trazara todas las posibilidades de signo/ cero para f′ y f′′, e identificar cuáles dan información definitiva sobre los extremos de f.

Hay nueve posibilidades de la siguiente manera:

f′	f′′	¿Información definitiva de Extrema?
+	+	No
+	−	No
+	0	No
−	+	No
−	−	No
−	0	No
0	+	Sí
0	−	Sí
0	0	No

Sólo cuando hay un punto crítico con f′=0 podemos usar la información de f′′ para decir si tenemos un mínimo o un máximo de f.

Ejemplo 2

Para la función\( f(x)= \frac{x^2−4x+4}{x^2+1} \nonumber\), busque todos los valores críticos, los valores y correspondientes para cada valor crítico, y clasifique cada punto como un máximo relativo o un mínimo relativo

El derivado es:\( f′(x)= \frac{2(2x^2−3x−2)}{(x^2+1)^2} \nonumber\)

Lo que da valores críticos: x=−12 y x=2

Esto significa que:\( f(−\frac{1}{2})=5 \nonumber\) y\( f(2)=0 \nonumber\)

La segunda derivada es:\( f′′(x)=− \frac{2(4x^3+9x^2+4x+5)}{(x^2+1)^3} \nonumber\)

La evaluación en los puntos críticos determina eso\( f′′(−\frac{1}{2})<0 \nonumber\), lo que significa cóncavo hacia abajo (un máximo), y f′′ (2) >0 significa cóncavo hacia arriba (un mínimo).

El gráfico de funciones se representa a continuación:

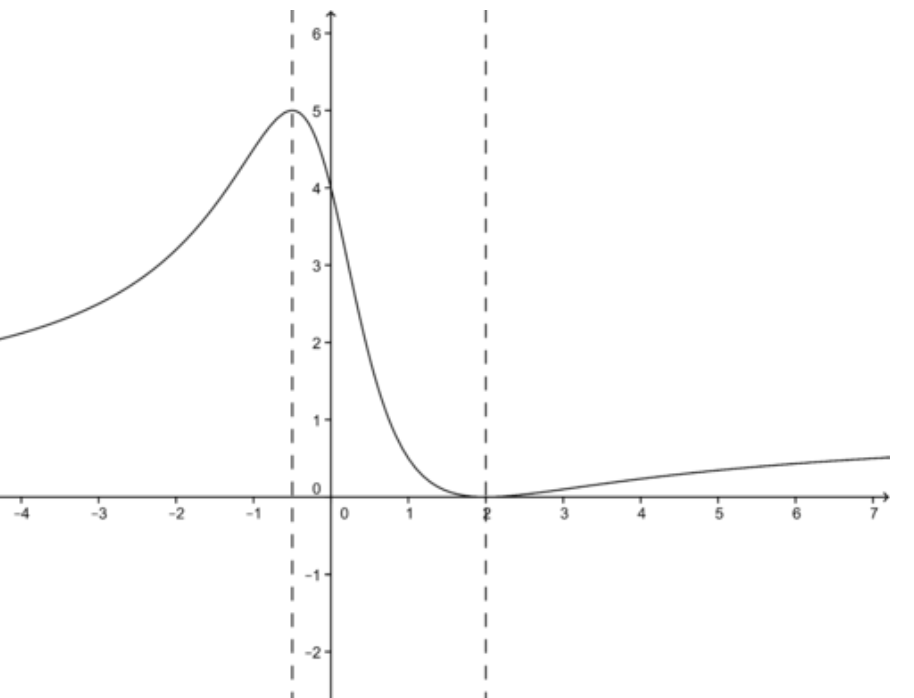
CC BY-NC-SA

Ejemplo 3

Para la función\( f(x)=2x^4−3x^2+2 \nonumber\), encuentre todos los valores críticos, clasifique cada punto como máximo relativo o mínimo relativo e identifique cualquier punto de inflexión

El derivado es:\( f′(x)=8x^3−6x \nonumber\)

Lo que da valores críticos: x=0 y\( x=± \frac{ \sqrt{3}}{2} \nonumber\)

La segunda derivada es:\( f′′(x)=24x^2−6 \nonumber\)

La evaluación en los puntos críticos determina que f′′ (0) <0, lo que significa cóncavo hacia abajo (un máximo), y\( f′′(± \frac{\sqrt{3}}{2})>0 \nonumber\) significa cóncavo hacia arriba (dos mínimos).

La segunda derivada es 0 cuando\( 24x^2−6=6(2x−1)(2x+1)=0 \nonumber\).

x=0 y x=±12 son puntos de inflexión.

 

---

Revisar

Para el #1 -8, encuentra los puntos críticos, determina si cada uno es un mínimo o máximo local, y determina cualquier punto de inflexión.

1. \( f(x)=x^3−3x^2+1 \nonumber\)
2. \( f(x)=x^4−2x^3−x+2 \nonumber\)
3. \( f(x)=sin2x \nonumber\)en el intervalo\( [0,\frac{π}{2}] \nonumber\).
4. \( f(x)=\frac{1}{x^2−x+2} \nonumber\)
5. \( f(x)=2x^3−3x^2+6x \nonumber\)
6. \( f(x)=x^3−12x+5 \nonumber\)en el intervalo [-5, 3]
7. \( f(x)=x^5+20x+5 \nonumber\)
8. \( f(x)=x2−5x+6, (-1, 3] \nonumber\)
9. Encuentra el máximo absoluto y el mínimo absoluto de\( f(x)=x^3−3x^2+2 \nonumber\) en el intervalo [0, 4].

Para #10 -15, encuentra los puntos críticos y los mínimos y máximos locales.

10. \( f(x)=x^2e^{−x} \nonumber\)
11. \( f(x)=\frac{x^2}{x−1} \nonumber\)
12. \( f(x)=5e^{−x}+x^3 \nonumber\)
13. \( f(x)=e^{−2x}+e^x \nonumber\)
14. \( f(x)=3^xe^{−x} \nonumber\)
15. \(  f(x)=xtanx \nonumber\)en el intervalo\(  [−π,π] \nonumber\).

---

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.6.

---

El vocabulario

Término	Definición
concavidad	La concavidad describe el comportamiento de la pendiente de la línea tangente de una función de tal manera que la concavidad es positiva si la pendiente está aumentando, negativa si la pendiente es decreciente, y cero si la pendiente es constante.
función decreciente	Una función decreciente es aquella con una gráfica que baja de izquierda a derecha.
prueba de primera derivada	La primera prueba derivada dice que si f es una función continua y que x=c es un valor crítico de f, entonces si f′ cambia de positivo a negativo en x=c entonces f tiene un máximo local en x=c, si f′ cambia de negativo a positivo en x=c entonces f tiene un mínimo local en x=c, y si f′ no cambia signo en x=c entonces f no tiene ni un máximo local ni mínimo a x=c.
aumentar la función	Una función creciente es aquella con una gráfica que sube de izquierda a derecha.
punto de inflexión	Un punto de inflexión es un punto en el dominio donde la concavidad cambia de positiva a negativa o negativa a positiva.
prueba de segunda derivada	La segunda prueba derivada dice que si f es una función continua cerca de c y c es un valor crítico de f, entonces si f′′ (c) = 0 <0 then f has a relative maximum at x=c, if f′′ (c) > entonces f tiene un mínimo relativo a x=c, y si f′′ (c) =0 entonces la prueba no es concluyente y x=c puede ser un punto de inflexión.

---

Recursos adicionales

Video: Concavidad e Inflexión Resuelta

Práctica: Concavidad e Inflexión