9.5: Aproximaciones Trapezoidales y de Punto Medio
- Page ID
- 105901
Recordemos que hemos utilizado diferentes formas para aproximar el valor de las integrales. Estos incluyeron Sumas de Riemann usando extremos izquierdo y derecho, así como puntos medios para encontrar la longitud de cada baldosa rectangular. En esta lección las baldosas rectangulares son reemplazadas por baldosas trapezoidales para aproximarse a la integral. ¿Crees que el uso de trapecios daría un resultado más preciso que el uso de rectángulos? ¿Por qué? ¿Se te ocurre alguna razón por la que la concavidad de la curva de función importaría en la precisión de la estimación del área usando trapecios?
Recordemos que empleamos diferentes formas de aproximar el valor de las integrales. Estos incluyeron Sumas de Riemann usando extremos izquierdo y derecho, así como puntos medios para encontrar la longitud de cada baldosa rectangular. En esta lección aprenderemos otros dos métodos para aproximar integrales. El primero de ellos, la Regla Trapezoidal, utiliza áreas de tejas trapezoidales para aproximarse a la integral. El segundo método, la Regla de Simpson, utiliza parábola para hacer la aproximación.
Recordemos cómo usaríamos la regla de punto medio con n=4 rectángulos para aproximar el área bajo la gráfica\( f(x)=x^2+1 \nonumber\) de x=0 a x=1.
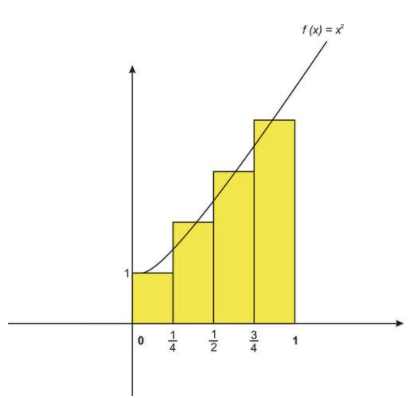
CC BY-NC-SA
Si en lugar de usar el valor de punto medio dentro de cada subintervalo para encontrar la longitud del rectángulo correspondiente, podríamos haber formado trapecios uniendo los valores máximo y mínimo de la función dentro de cada subintervalo:
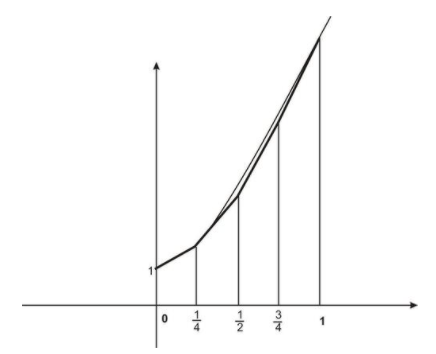
CC BY-NC-SA
El área de un trapecio es\( A= \frac{h(b_1+b_2)}{2} \nonumber\), donde b1 y b2 son las longitudes de los lados paralelos y h es la altura. En nuestros trapezoides la altura es ∆x y b1 y b2 son los valores de la función. Por lo tanto, al encontrar las áreas de los trapecios, en realidad promediamos los extremos izquierdo y derecho de cada subintervalo.
Por lo tanto, un trapecio típico tendría el área
\[ A = \frac{△x}{2} (f(x_{i−1})+f(x_i)) \nonumber\].
Para aproximar\ (\ int\ limits_a^b f (x) dx con n de estos trapezoides, tenemos
\[ \int\limits_a^b f(x)dx ≈ \frac{1}{2} [|\sum_{i=1}^n f(x_{i−1})△x+ \sum_{i=1}^n f(x_i)△x] \nonumber\]
\[ = \frac{△x}{2} [f(x_0)+f(x_1)+f(x_1)+f(x_2)+f(x_2)+⋯+f(x_{n−1})+f(x_n)] \nonumber\]
\[ = \frac{△x}{2} [f(x_0)+2f(x_1)+2f(x_2)+⋯+2f(x_{n−1})+f(x_n)],△x= \frac{b−a}{n} \nonumber\].
Aplica la fórmula de arriba y usa la Regla Trapezoidal para aproximarse\( \int\limits_0^3 x^2dx \nonumber\) con n=6.
Cada subintervalo es\( △x= \frac{b−a}{n}= \frac{3−0}{6}= \frac{1}{2} \nonumber\).
La aproximación integral es:
\[ \int\limits_0^3 x^2 dx ≈ \frac{1}{4} [f(0)+2f( \frac{1}{2})+ 2 f (1)+ 2 f ( \frac{3}{2})+2f(2)+2f( \frac{5}{2})+f(3)] \nonumber\]
\[ = \frac{1}{4} [0+(2⋅ \frac{1}{4})+(2⋅1)+(2⋅ \frac{9}{4})+(2⋅4)+(2⋅ \frac{25}{4} )+9] \nonumber\]
\[ = \frac{1}{4} [ \frac{73}{2}]= \frac{73}{8} = 9.125. \nonumber\]
Se puede determinar una solución exacta usando el antiderivado con el Teorema Fundamental.
\[ \int\limits_0^3 x^2 dx = \frac{x^3}{3} |_0^3 = 9 . \nonumber\]
El error es de aproximadamente 1.4%.
Para algunas integrales es imposible encontrar una antiderivada y un método numérico es la única opción.
Cuando este es el caso, la precisión de la aproximación es un problema. En particular, ¿qué tan grande debe ser n para que la estimación trapezoidal sea precisa dentro de un valor dado, digamos 0.001?
La magnitud del error al usar la técnica trapezoidal para un valor dado de n puede mostrarse como:
\[ |Error_{Trapezoidal} | ≤ \frac{k(b−a)^3}{12 n^2}, \mbox{ where } |f′′(x)|≤k \mbox{ for } a≤x≤b \nonumber\]
Esto significa que la elección\( n ≥ \sqrt{ \frac{k(b−a)^3}{12} ⋅ |Error_{Trapezoidal}| } \nonumber\) cumplirá o superará un error especificadoErrorTrapezoidal.
Encuentra n para que la Estimación Trapezoidal para\( \int_0^3 x^2 dx \nonumber\) sea precisa de 0.001.
Tenemos que encontrar n tal que\( |Error_{Trapezoidal}| ≤ 0.001 \nonumber\).
Primero tenga en cuenta que\( |f′′(x)|=2 \mbox{ for } 0≤x≤3 \nonumber\). De ahí que podamos tomar k=2 para encontrar nuestro límite de error.
\[ |Error_{Trapezoidal}| ≤ \frac{2 (3−0)^3}{12 n^2} = \frac{54}{12 n^2} \nonumber\]
Tenemos que resolver la siguiente desigualdad para n:
\[ \frac{54}{12n^2} < 0.001, \nonumber\]
\[ n^2 > \frac {54}{12(0.001)}, \nonumber\]
\[ n > \sqrt{ \frac{54}{12(0.001)}} ≈ 67.08 \nonumber\]
De ahí que debemos tomar n=68 para lograr la precisión deseada.
Ejemplos
Ejemplo 1
Anteriormente, se le preguntó si cree que usar trapecios para aproximar el área bajo una curva daría un resultado más preciso que usar rectángulos. ¿Se te ocurre alguna razón por la que la concavidad de la curva de función importaría en la precisión de la estimación del área usando trapecios?
Si piensas que el uso de trapecios daría un resultado más preciso (con número de subintervalos igual) estás en lo cierto. Con algunos ejemplos, se puede ver visualmente que los trapezoides cubren mejor el área bajo la curva. Observe, sin embargo, que si la curva de función es cóncava hacia arriba, los trapezoides sobreestimarán el área; si la concavidad está abajo, los trapezoides subestimarán el área.
Ejemplo 2
Utilice la Regla Trapezoidal para aproximarse a 02x3dx para n=4. Redondea la respuesta a cuatro decimales y compara este valor con el valor exacto de la integral. ¿Cuál es el error esperado para n=4?
Encontramos cada subintervalo como ∆x=b−an=2−04=12.
La aproximación integral se evalúa de la siguiente manera:
\[ \int\limits_0^2 x^3 dx ≈ \frac{1}{4} [f(0) + 2 f(0.5) + 2 f(1) + 2 f(1.5) + f(2) ] \nonumber\]
\[ ≈ \frac{1}{4} [0+2⋅0.125+2⋅1+2⋅3.375+8] \nonumber\]
\[ \int\limits_0^2 x^3 dx ≈ 4.25 \nonumber\]
La estimación de la integral es de 4.25.
El valor exacto de la integral:\( \int\limits_0^2 x^3 dx = \frac{x^4}{4}|_0^2 = 4 \nonumber\).
El error entre estos es 0.25.
El error esperado usando n=4:
Para f′′ (x) =6x, f′′ (x) ≤62=12 en el intervalo [0,2].
Por lo tanto,\( |Error_{Trapezoidal}| ≤ \frac{k(b−a)^3}{12 n^2} = \frac{12(2)^3}{12⋅4^2}=0.5 \nonumber\).
El error real es menor que\( |Error_{Trapezoidal}| \nonumber\).
Ejemplo 3
Utilice la Regla Trapezoidal para aproximarse\( \int\lim_1^2 \frac{1}{(x+1)^2} dx \nonumber\) para n=4. Redondea la respuesta a cuatro decimales y compara este valor con el valor exacto de la integral. ¿Cuál es el error esperado para n=4?
Encontramos cada subintervalo como\( △x = \frac{b−a}{n} = \frac{2−1}{4} = \frac{1}{4} \nonumber\).
La aproximación integral se evalúa de la siguiente manera:
\[ \int\limits_1^2 \frac{1}{(x+1)^2} dx ≈ \frac{1}{8} [f(2)+2f(2.25)+2f(2.5)+2f(2.75)+f(3)] \nonumber\]
\[ ≈ \frac{1}{8} [\frac{1}{4} + 2 \frac{1}{2.25^2} + 2 \frac{1}{2.5^2} + 2 \frac{1}{2.75^2} + \frac{1}{3^2} ] \nonumber\]
\[ ≈ \frac{1}{8} [0.25+0.39506+0.32+0.26446+0.11111] \nonumber\]
\[ \int\limits_1^2 \frac{1}{(x+1)^2} dx ≈ 0.16758 ≈ 0.1676 \nonumber\]
La estimación de la integral es 0.1676.
El valor exacto de la integral:\[ ∫121(x+1)2dx=−1x+1∣∣∣21=16=0.16⎯⎯⎯ \nonumber\].
El error entre estos es 0.0009.
El error esperado usando n=4:
Para\( f′′(x) = \frac{6}{(x+1)^4}, f′′(x) ≤ \frac{6}{(1+1)^4} = \frac{3}{8} = 0.375 \nonumber\) en el intervalo [1, 2].
Por lo tanto,\(|Error_{Tropezoidal}| ≤ \frac{k(b−a)^3}{12n^2} = \frac{0.375(1)^3}{12⋅4^2} = 0.001953 \nonumber\).
El error real es menor que\( |Error_{Trapeziodal}| \nonumber\).
Revisar
Utilice la Regla Trapezoidal para aproximar las integrales definidas usando el número dado de subintervalos n.
- \( \int_1^7 (x+7)dx \mbox{ with } n=6 \nonumber\).
- \( \int_{−2}^2 (x+4)dx \mbox{ with } n=4 \nonumber\).
- \( \int_{−4}{1} (−x^2−2x+8) dx \mbox{ with } n=5 \nonumber\).
- \( \int_2^7 \frac{2}{x} dx \mbox{ with } n=5 \nonumber\).
- \( \int_0^2 x^4 dx \mbox{ with } n=4 \nonumber\).
- \( \int_0^1 sin \frac{x}{2} dx \mbox{ with } n=4 \nonumber\).
- \( \int_2^4 \sqrt{x} dx \mbox{ with } n=5 \nonumber\).
- \( \int_0^1 x^2e−xdx \mbox{ with } n=8 \nonumber\).
- \( \int_1^4 ln\sqrt{x} dx \mbox{ with } n=6 \nonumber\).
- \( \int_0^1 \sqrt{1+x^4}dx \mbox{ with } n=4 \nonumber\).
- \( \int_1^3 \frac{1}{x} dx \mbox{ with } n=8 \nonumber\).
- \( \int_0^2 x^3 dx \mbox{ for } n=8 \nonumber\).
- Encuentre un valor de n que garantice un error de no más de 10−5 en la aproximación Trapezoidal de\( \int_2^4 \sqrt{x} dx \nonumber\). ¿Qué tan grande debe ser n para que la Estimación Trapezoidal para\( \int_1^3 \frac{1}{x} dx \nonumber\) sea precisa dentro de:
- ¿0.001?
- 0.00001?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.10.
El vocabulario
| Término | Definición |
|---|---|
| regla trapezoidal | La regla trapezoidal es un método para calcular una integral definida mediante el cálculo de los segmentos trapezoidales de área en el intervalo de integración y sumarlos. |
Recursos adicionales
PLIX: Juega, aprende, interactúa, explora - Área de una falda
Video: Aproximación trapezoidal del área bajo la curva por Khan Academy

