1.6: Puntos que particionan segmentos de línea
- Page ID
- 107609
La fórmula de sección busca las coordenadas de un punto que divide un segmento de línea en una proporción dada.
Recordemos que una mediana de un triángulo es un segmento de línea que conecta un vértice del triángulo con el punto medio del lado opuesto al vértice. Todos los triángulos tienen tres medianas y estas tres medianas se cruzan en un punto llamado centroide, que se muestra a continuación. El centroide divide cada mediana en una proporción 2:1.
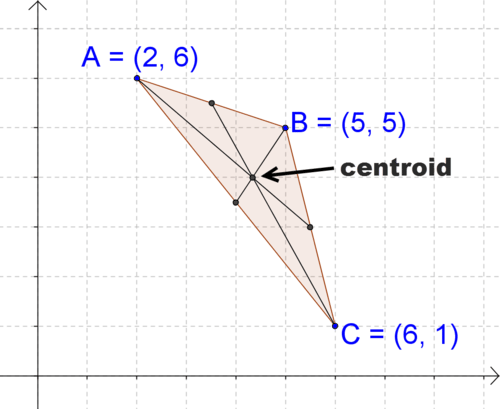 Figura\(\PageIndex{1}\)
Figura\(\PageIndex{1}\)Encuentra las coordenadas del centroide, dadas las coordenadas de los vértices del triángulo como se muestra.
Particiones
Supongamos que tiene un segmento de línea\(\overline{AB}\). Un punto\(P\) divide este segmento de línea en dos partes tales que\(AP=mk\) y\(PB=nk\). Se puede decir que\(P\) las particiones de punto segmentan\(AB\) en una\(m:n\) proporción. (Tenga en cuenta que\(\dfrac{mk}{nk}=mn\), una proporción de\(m:n\).)
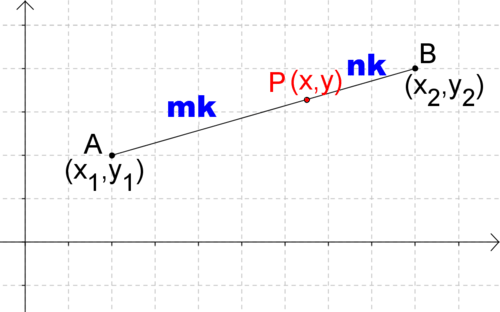 Figura\(\PageIndex{2}\)
Figura\(\PageIndex{2}\)Una pregunta natural es, ¿cuáles son las coordenadas de punto\(P\)? Resulta que con la ayuda de triángulos y álgebra similares, se puede llegar a una fórmula que le dará las coordenadas de punto en\(P\) función de las coordenadas de\(A\), las coordenadas de\(B\), y la relación\(m:n\). Esta fórmula a veces se denomina fórmula de sección.
Fórmula de sección: Dado\(\overline{AB}\) con\(A=(x_1, y_1)\) y\(B=(x_2, y_2)\), si\(P\) las particiones de punto\(\overline{AB}\) en una\(m:n\) relación, entonces las coordenadas del punto P son:
\(P=\left (\dfrac{mx_{2}+nx_{1}}{m+n}, \dfrac{my_{2}+ny_{1}}{m+n}\right )\)
Demostrando similitud de triángulo
Para el segmento\(\overline{AB}\) inferior, dibuje dos triángulos rectos, uno con hipotenusa\(\overline{AP}\) y otro con hipotenusa\(\overline{PB}\). Demostrar que estos triángulos son similares.
 Figura\(\PageIndex{3}\)
Figura\(\PageIndex{3}\)Comienza dibujando los triángulos rectos. Abajo, la base y la altura de cada triángulo han sido etiquetadas en verde.
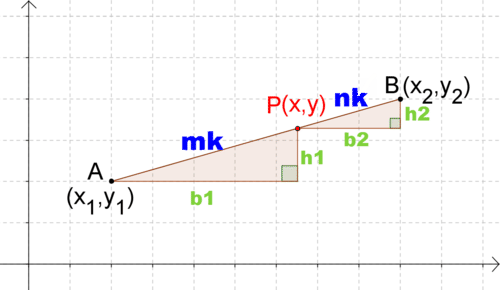 Figura\(\PageIndex{4}\)
Figura\(\PageIndex{4}\)Claramente estos triángulos tienen un par de ángulos congruentes (los ángulos rectos). ¿Qué otra información tienes sobre los triángulos? Sabes que para cada triángulo, la relación\(\dfrac{height}{base}\) es la pendiente de\(\overline{AB}\). Debido a que estos dos triángulos están unidos al mismo segmento de línea con la misma pendiente, significa que\(\dfrac{h_1}{b_1} = {h_2}{b_2}\). Esto equivale a\(\dfrac{b_2}{b_1}=\dfrac{h_2}{h_1}\). Dos pares de lados están en la misma proporción.
No sólo hay un par de ángulos congruentes, sino que también hay dos pares de lados correspondientes con la misma proporción. Los triángulos son similares por\(SAS\) ∼.
Encontrar longitud y altura
Encuentra las longitudes de las bases y alturas de cada triángulo. Usa el hecho de que los triángulos son similares a configurar y resolver proporciones para\(x\) y luego para para para\(y\) encontrar las coordenadas de punto\(P\).
 Figura\(\PageIndex{5}\)
Figura\(\PageIndex{5}\)Las bases y alturas se pueden encontrar en términos de\(x_1\),\(y_1\),\(x\),\(y\),\(x_2\),\(y_2\).
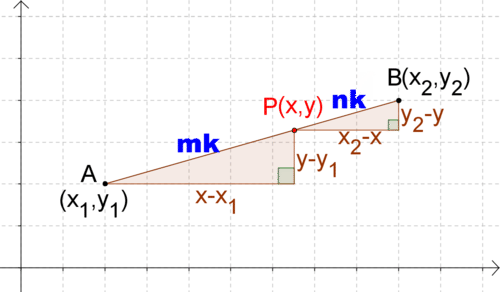 Figura\(\PageIndex{6}\)
Figura\(\PageIndex{6}\)Debido a que los triángulos son similares, las relaciones entre pares de lados correspondientes son iguales. En particular, ya sabes:
- \(\dfrac{mk}{nk}=\dfrac{x−x_1}{x_2−x}\)
- \(\dfrac{mk}{nk}=\dfrac{y−y_1}{y_2−y}\)
Puede usar álgebra para resolver la primera ecuación para\(x\) y la segunda ecuación para\(y\).
- \(\dfrac{mk}{nk}=\dfrac{x−x_1}{x_2−x}\)\(\rightarrow \dfrac{m}{n}=\dfrac{x−x_1}{x_2−x} \)
\(\rightarrow mx_2−mx=nx−nx_1\)
\(\rightarrow mx_2+mx_1=mx+nx \)
\(\rightarrow mx_2−nx_1=x(m+n)\)
\(\rightarrow \dfrac{mx_2−nx_1}{m+n}=\dfrac{x(m+n)}{m+n}\)
\(\rightarrow x=\dfrac{mx_2+nx_1}{m+n}\)
- \(\dfrac{mk}{nk}=\dfrac{y−y_1}{y_2−y}\)\(\rightarrow\dfrac{m}{n}=\dfrac{y−y_1}{y_2−y} \)
\(\rightarrow my_2−my=ny−ny_1\)
\(\rightarrow my_2+my_1=my+ny\)
\(\rightarrow my_2−ny_1=y(m+n)\)
\(\rightarrow \dfrac{my_2−ny_1}{m+n}=\dfrac{y(m+n)}{m+n}\)
\(\rightarrow x=\dfrac{my_2+ny_1}{m+n}\)
\(P\)El punto está en:
\(P=\left(\dfrac{mx_2+nx_1}{m+n} ,\dfrac{my_2+ny_1}{m+n}\right)\)
Encontrar las coordenadas de un punto
Considere\(\overline{AB}\) con\(A=(10, 2)\) y\(B=(4, 1)\). \(P\)particiones\(\overline{AB}\) en una proporción de\(2:3\). Encuentra las coordenadas de punto\(P\).
Puede usar la fórmula de sección con\((x_1,y_1)=(10, 2)\),\((x_2, y_2)=(4, 1)\),\(m=2\),\(n=3\).
\(P=\left(\dfrac{mx_2+nx_1}{m+n} ,\dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{2 \cdot 4+3 \cdot10}{2+3}, \dfrac{2 \cdot 1+3\cdot 2}{2+3}\right)=\left(7.6,1.6\right)\)
Se pueden trazar puntos\(A\)\(B\),, y\(P\) para ver si esta respuesta es realista.
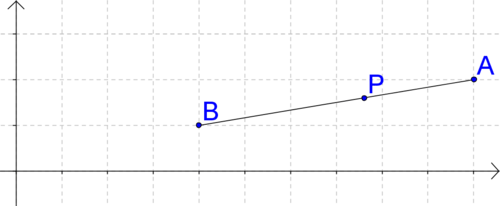 Figura\(\ PageIndex {7}\)
Figura\(\ PageIndex {7}\)Esto sí se ve como\(P\) partitions the segment from \(A\) to \(B\) in a ratio of \(2:3\). Note that the answer would be different if you were looking for the point that partitioned the segment from \(B\) to \(A\). The order of the letters and “direction” of the segment matters.
Example \(\PageIndex{1}\)
Earlier, you were asked to find the coordinates of the centroid, given the coordinates of the vertices of the triangle as shown.
 Figure \(\PageIndex{8}\)
Figure \(\PageIndex{8}\)Solution
One way to find the coordinates of the centroid is to use the section formula. You can focus on any of the three medians. Here, look at the median from point A. First, you will need to find the coordinates of the midpoint of \(\overline{BC}\) (the midpoint formula, a special case of the section formula, is derived in Guided Practice #1 and #2):
\(\left(\dfrac{x_2+x_1}{2}, \dfrac{y_2+y_1}{2}\right)=\left (\dfrac{5+6}{2}, \dfrac{5+1}{2}\right)=\left(5.5,3\right )\)
\(\left(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{2 \cdot 5.5+1 \cdot 2}{2+1}, \dfrac{2 \cdot 3+1 \cdot 6}{2+1}\right)=\left(\dfrac{13}{3}, 4\right)\)
Looking at the picture, these coordinates for the centroid are realistic.
Example \(\PageIndex{2}\)
The midpoint of a line segment is the point exactly in the middle of the line segment. In what ratio does a midpoint partition a segment?
Solution
1:1, because the segments connecting the midpoint to each endpoint will be the same length.
Example \(\PageIndex{3}\)
The midpoint formula is a special case of the section formula where m=n=1. Derive a formula that calculates the midpoint of the segment connecting \((x_1,y_1)\) with \((x_2, y_2)\).
Solution
For a midpoint, \(m=n=1\). The section formula becomes:
\(\left(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{x_2+x_1}{2}, \dfrac{y_2+y_1}{2}\right)
This is the midpoint formula.
Example \(\PageIndex{4}\)
Consider \(\overline{BA}\) with \(B=(4, 1)\) and \(A=(10, 2)\). \(P\) partitions the segment in a ratio of \(2:3\). Find the coordinates of point \(P\). How and why is this answer different from the answer to Example \(C\)?
Solution
\((x_1, y_1)=(4,1)\) and \((x_2, y_2)=(10,2)\). \(m=2\) and \(n=3\).
\(P=\left(\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right)=\left(\dfrac{2 \cdot 10+3 \cdot 4}{2+3}, \dfrac{2 \cdot 2+3 \cdot 1}{2+3}\right)=\left(6.4,1.4\right)\)
This answer is different from the answer to Example C because in this case point P is partitioning the segment in a \(2:3\) ratio starting from point \(B\). In Example \(C\), you were starting from point \(A\).
Review
Find the midpoint of each of the following segments defined by the given endpoints.
1. \((2, 6)\) and \((−4, 8)\)
2. \((1, 9)\) and \((−2, 5)\)
3. \((11, 24)\) and \((8, 12)\)
4. \((1, 3)\) is the midpoint of \(\overline{AB}\) with \(A=(−2, 1)\). Find the coordinates of \(B\).
5. \((2, 4)\) is the midpoint of \(\overline{CD}\) with \(C=(−5, 9)\). Find the coordinates of \(D\).
6. \((4, 23)\) is the midpoint of \(\overline{EF}\) with \(E=(7, 11)\). Find the coordinates of \(F\).
Consider \(A=(−9, 4)\) and \(B=(11, 17)\).
7. Point \(P_1\) partitions the segment from \(A\) to \(B\) in a \(3:5\) ratio. Find the coordinates of point \(P_1\).
8. Point \(P_2\) partitions the segment from \(B\) to \(A\) in a \(3:5\) ratio. Find the coordinates of point \(P_2\).
9. Why are the answers to 7 and 8 different?
10. Find the length of \(AP_1\) and \(P_2B\). Why should these lengths be the same?
Consider \(C=(−6, −1)\) and \(D=(4, 8)\).
11. Point \(P_3\) partitions the segment from \(A\) to \(B\) in a \(1:2\) ratio. Find the coordinates of point \(P_3\).
12. Point \(P_4\) partitions the segment from \(B\) to \(A\) in a \(4:5\) ratio. Find the coordinates of point \(P_4\).
13. Point \(P=(1, 2)\) partitions the segment from \(E=(9, 6)\) to \(F\) in a \(2:5\) ratio. Find the coordinates of point F.
14. Point \(P=(−6, −4)\) partitions the segment from \(G=(−4, 6)\) to \(H\) in a \(5:3\) ratio. Find the coordinates of point \(H\).
15. Point \(P=(6,8)\) partitions the segment from \(I=(−2,1)\) to \(J\) in a \(6:7\) ratio. Find the coordinates of point \(J\).
16. A triangle is defined by the points \((5, 6)\), \((9, 17)\), and \((−2, 1)\). Find the coordinates of the centroid of the triangle.
Review (Answers)
To see the Review answers, open this PDF file and look for section 10.6.
Vocabulary
| Term | Definition |
|---|---|
| centroid | The centroid is the point of intersection of the medians in a triangle. |
| Median | The median of a triangle is the line segment that connects a vertex to the opposite side's midpoint. |
| midpoint | The midpoint of a line segment is the point on the line segment that splits the segment into two congruent parts. |
| Midpoint Formula | The midpoint formula says that for endpoints \((x_{1},y_{1})\) and \((x_{2},y_{2})\), the midpoint is \(\left (\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)\). |
| Partitions | To partition is to divide into parts. |
| Section Formula | The section formula states how to find the coordinates of a point that partitions a line segment in a given ratio. |
Additional Resource
Interactive Element
Practice: Points that Partition Line Segments

