1.11: Ángulos congruentes y bisectores angulares
- Page ID
- 107597
Ángulos de la misma medida, y líneas o porciones de líneas que dividen los ángulos en dos mitades iguales.
Cuando dos figuras geométricas tienen la misma forma y tamaño (o la misma medida de ángulo en el caso de los ángulos) se dice que son congruentes.
| Etiquetarlo | Dilo |
|---|---|
| \(\angle ABC \cong \angle DEF\) | \(ABC\)El ángulo es congruente con el ángulo\(DEF\). |
Si dos ángulos son congruentes, entonces también son iguales. Para etiquetar ángulos iguales utilizamos marcas de ángulo, como se muestra a continuación:
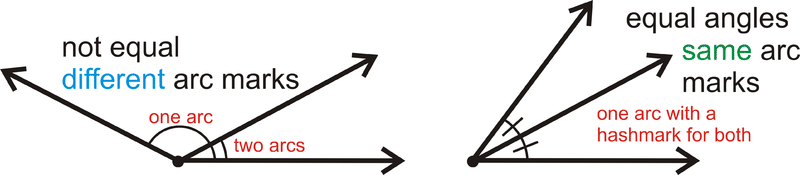Figura\(\PageIndex{1}\)Una bisectriz angular es una línea, o una porción de una línea, que divide un ángulo en dos ángulos congruentes, teniendo cada uno una medida exactamente la mitad del ángulo original. Cada ángulo tiene exactamente un ángulo bisectriz.
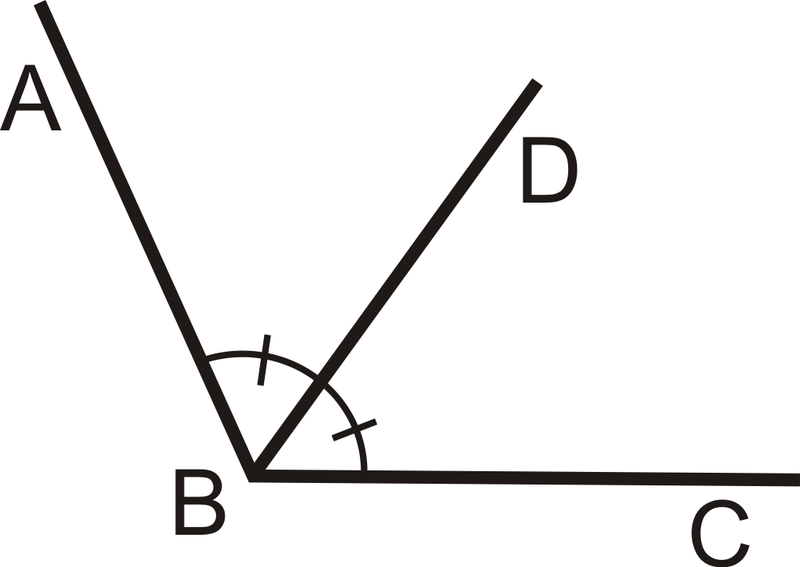Figura\(\PageIndex{2}\)En la imagen de arriba,\(\overline{BD}\) se encuentra el ángulo bisectriz de\(\angle ABC\), así\(\angle ABC \cong \angle DBC\) y\(m \angle ABD \cong \dfrac{1}{2} m \angle ABC\).
¿Y si te dijeran que un segmento de línea divide un ángulo por la mitad? ¿Cómo encontrarías las medidas de los dos nuevos ángulos formados por ese segmento?
Para los Ejemplos 1 y 2, copie la siguiente figura y etiquétala con la siguiente información:
Figura\(\PageIndex{3}\)Ejemplo\(\PageIndex{1}\)
\(\angle A \cong \angle C\)
Solución
Debe tener las marcas correspondientes en\(\angle A\) y\(\angle C\).
Ejemplo\(\PageIndex{2}\)
\(\angle B \cong \angle D\)
Solución
Debes tener las marcas correspondientes en\(\angle B\) y\(\angle D\) (que se vean diferentes de las marcas que hiciste en el Ejemplo 1).
Ejemplo\(\PageIndex{3}\)
Escribe todas las declaraciones de igual ángulo.
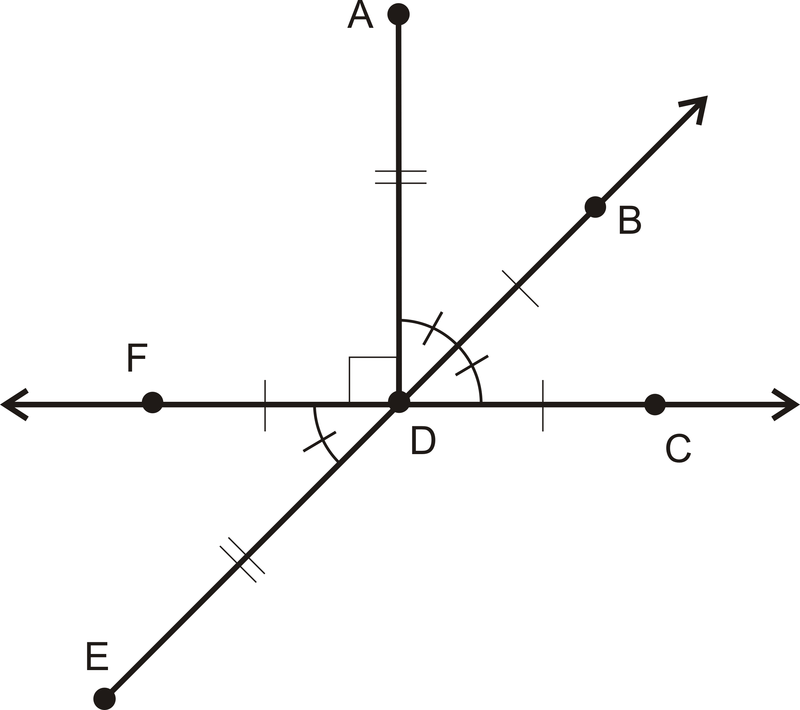Figura\(\PageIndex{4}\)Solución
\(m \angle ADB=m\angle BDC=m \angle FDE=45^{\circ}\)
\(m \angle ADF=m\angle ADC=90^{\circ}\)
Ejemplo\(\PageIndex{4}\)
¿Cuál es la medida de cada ángulo?
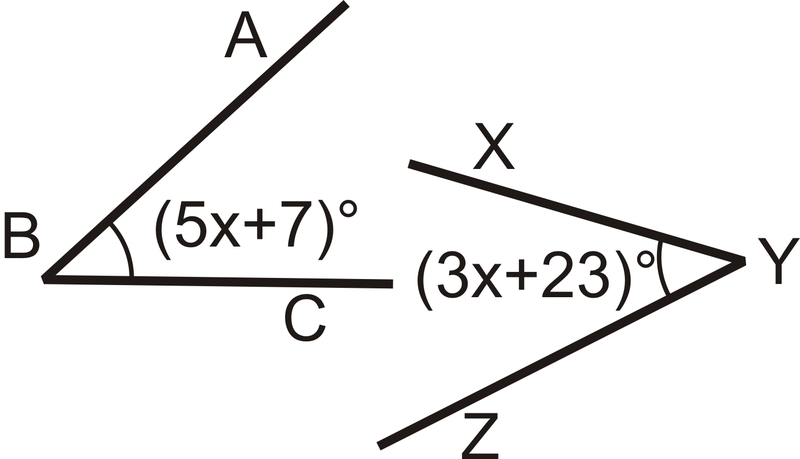Figura\(\PageIndex{5}\)Solución
De la imagen, vemos que los ángulos son iguales.
Establezca los ángulos iguales entre sí y resuelva.
\((5x+7)^{\circ} = (3x+23)^{\circ}\)
\((2x)^{\circ}= 16^{\circ}\)
\(x=8\)
Para encontrar la medida de\(\angle ABC\), conéctelo\(x=8\) a
\((5x+7)^{\circ} \rightarrow (5(8)+7)^{\circ} =(40+7)^{\circ}=47^{\circ}\).
Porque\(m \angle ABC=m \angle XYZ\),\(m \angle XYZ=47^{\circ}\) también.
Ejemplo\(\PageIndex{5}\)
¿Es\(\overline{OP}\) el ángulo bisectriz de\(\angle SOT\)?
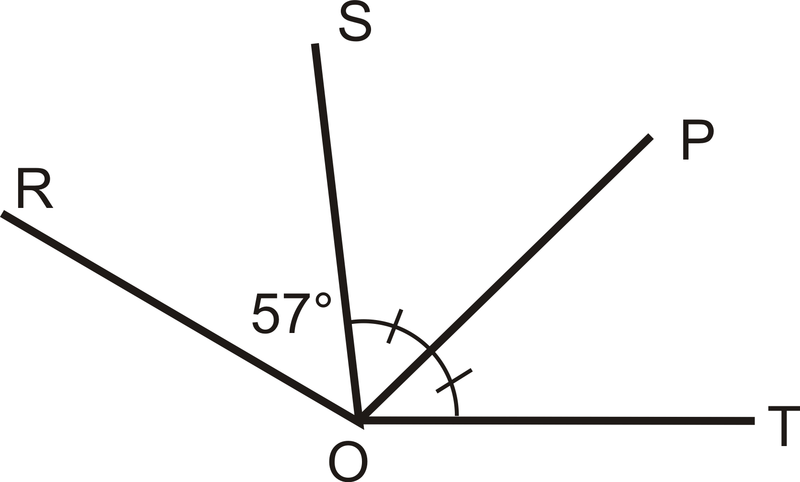Figura\(\PageIndex{6}\)Solución
Sí,\(\overline{OP}\) es el ángulo bisectriz\(\angle SOT\) de las marcas en la imagen.
Revisar
Para 1-4, use la siguiente imagen para responder a las preguntas.
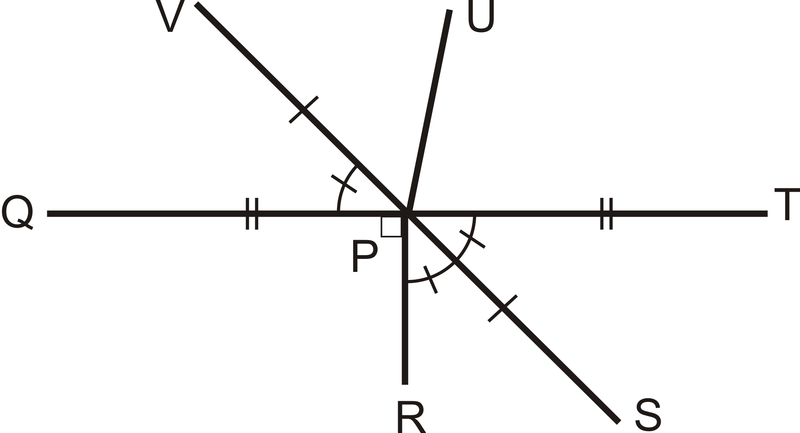Figura\(\PageIndex{7}\)- ¿De qué es la bisectriz angular\(\angle TPR\)?
- ¿Qué es\(m \angle QPR\)?
- ¿Qué es\(m \angle TPS\)?
- ¿Qué es\(m \angle QPV\)?
Para 5-6, use álgebra para determinar el valor de la variable en cada problema.
-
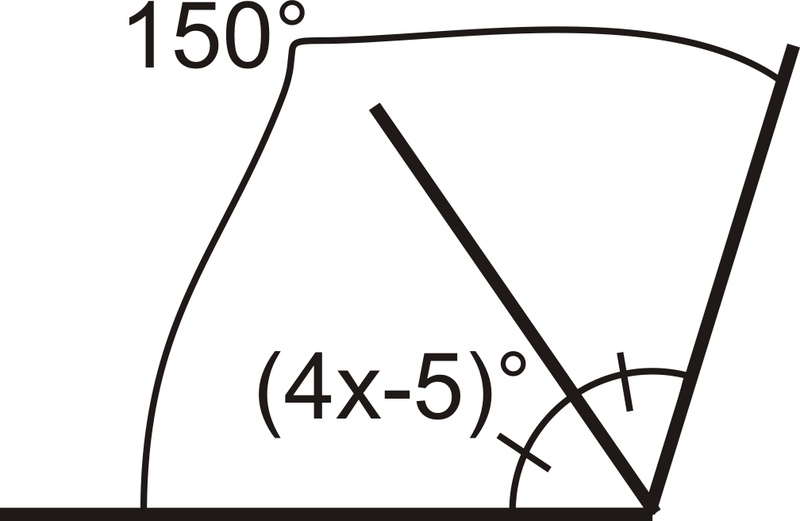Figura\(\PageIndex{8}\) -
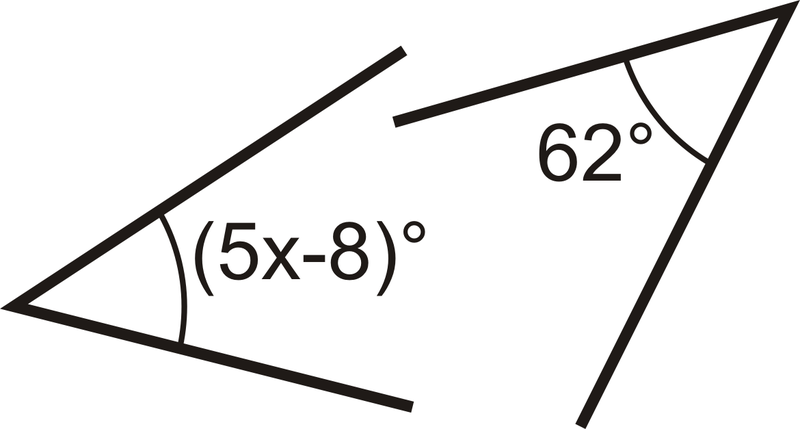Figura\(\PageIndex{9}\)
Para 7-10, decidir si la afirmación es verdadera o falsa.
- Cada ángulo tiene exactamente un ángulo bisectriz.
- Cualquier marca en un ángulo significa que el ángulo es\(90^{\circ}\).
- Un ángulo bisectriz divide un ángulo en tres ángulos congruentes.
- Los ángulos congruentes tienen la misma medida.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.3.
El vocabulario
| Término | Definición |
|---|---|
| bisectriz angular | Una bisectriz angular es un rayo que divide un ángulo en dos ángulos congruentes y más pequeños. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
Recurso Adicional
Elemento Interactivo
Video: Principios de ángulos congruentes y bisectores de ángulo - Básico
Actividades: Angulos congruentes y bisectores angulares Preguntas de Discusión
Ayudas de estudio: Guía de estudio de ángulos
Práctica: Ángulos congruentes y Bisectores de Ángulo
Mundo real: Noche estrellada