1.13: Propiedades del ángulo y teoremas
- Page ID
- 107646
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentre ángulos y segmentos de línea, y determine si las formas son congruentes y las líneas son paralelas. Comprender los ángulos complementarios como ángulos cuya suma es de 90 grados y los ángulos suplementarios como ángulos cuya suma es de 180 grados.
Medidas de pares de ángulos
Figura\(\PageIndex{1}\)Las líneas de falta de un diamante de béisbol se cruzan en el plato de casa para formar un ángulo recto. Un beisbol es impactado desde el plato de casa y forma un ángulo de\(36^{\circ}\) con la línea de falta de tercera base. ¿Cuál es la medida del ángulo entre la línea de falta de primera base y el baño del beisbol?
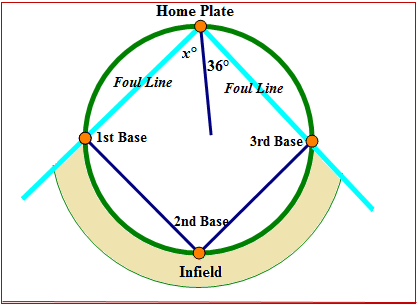Figura\(\PageIndex{2}\)¿Cómo puedes usar tus conocimientos de ángulos para averiguar la medida del ángulo?
En este concepto, aprenderás medida de pares de ángulos.
Pares de ángulos de medición
Existen diferentes tipos de pares de ángulos. Los ángulos verticales son un par de ángulos formado por líneas que se cruzan de tal manera que nunca son adyacentes. Tienen un vértice común y nunca comparten un lado común. Los ángulos verticales son iguales en medida. El siguiente diagrama muestra pares de ángulos verticales.
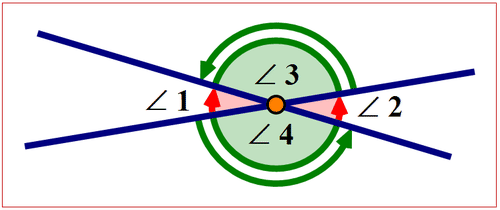Figura\(\PageIndex{3}\)\(\angle 1\)y\(\angle 2\) son ángulos verticales. \(m\angle 1=m\angle 2\)
\(\angle 3\)y\(\angle 4\) son ángulos verticales. \(m\angle 3=m\angle 4\)
Los ángulos adyacentes son un par de ángulos también formado por dos líneas que se cruzan. Los ángulos adyacentes están uno al lado del otro, tienen un vértice común y comparten un lado común. El siguiente diagrama muestra pares de ángulos adyacentes.
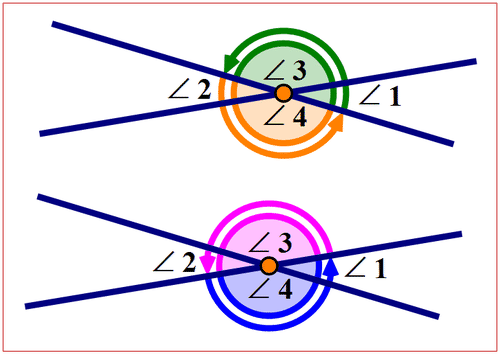Figura\(\PageIndex{4}\)Cada par de ángulos adyacentes forma un ángulo recto. Por lo tanto, la suma de dos ángulos adyacentes cualesquiera es igual\(180^{\circ}\).
\(m\angle 1+m \angle 3= 180^{\circ}\)
\(m\angle 2+m \angle 4= 180^{\circ}\)
\(m\angle 2+m \angle 3= 180^{\circ}\)
\(m\angle 1+m \angle 4= 180^{\circ}\)
Si la suma de dos ángulos es\(180^{\circ}\) entonces los ángulos se llaman ángulos suplementarios. El siguiente diagrama muestra dos ángulos suplementarios.
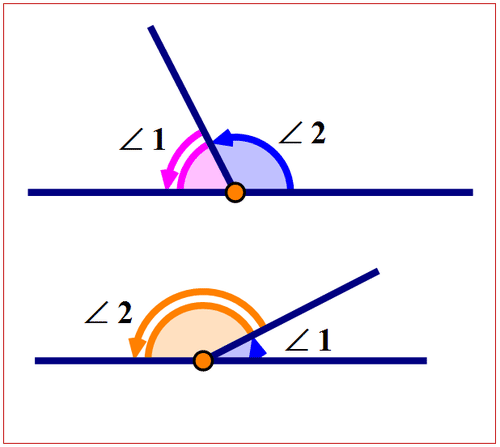Figura\(\PageIndex{5}\)En ambos diagramas,\(m\angle 1+m \angle 2= 180^{\circ}\).
Si la suma de dos ángulos es igual a 90° entonces los ángulos se denominan ángulos complementarios. El siguiente diagrama muestra dos ángulos complementarios.
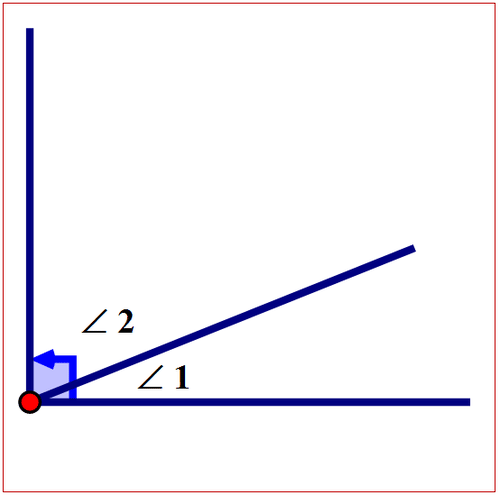Figura\(\PageIndex{6}\)\(m\angle 1+m \angle 2= 90^{\circ}\)
Apliquemos toda esta información sobre los ángulos y su medida para determinar la medida de\(\angle a\),\(\angle b\),\(\angle c\) en el siguiente diagrama.
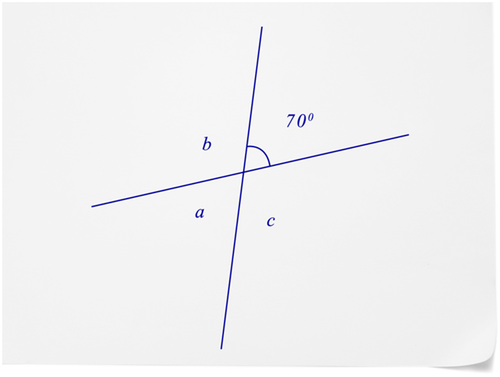Figura\(\PageIndex{7}\)Hay cuatro ángulos formados por líneas que se cruzan. La medida de uno de los ángulos es\(70^{\circ}\).
Primero, exponer la relación entre el ángulo de\(70^{\circ}\) y\(\angle b\).
El ángulo de\(70^{\circ}\). es adyacente\(\angle b\) y los dos ángulos forman un ángulo recto.
A continuación, expresar la relación usando símbolos.
\(\angle b+70^{\circ}=180^{\circ}\)
A continuación, restar 70° de ambos lados de la ecuación.
\(\angle b+70^{\circ}=180^{\circ}\)
\(\angle b+70^{\circ}- 70^{\circ}=180^{\circ}-70^{\circ}\)
Entonces, simplifique ambos lados de la ecuación.
\(\angle b+70^{\circ}- 70^{\circ}=180^{\circ}-70^{\circ}\)
\(\angle b = 110^{\circ}\)
La respuesta es\(110^{\circ}\).
\(m \angle b = 110^{\circ}\)
Primero, exponer la relación entre el ángulo de\(70^{\circ}\) y\(\angle a\).
El ángulo de\(70^{\circ}\) y\(\angle a\) son ángulos verticales y son iguales en medida.
A continuación, expresar la relación usando símbolos.
\(m\angle a=70^{\circ}\)
La respuesta es\(70^{\circ}\).
\(m\angle a=70^{\circ}\)
Primero exponer la relación entre el ángulo de\(70^{\circ}\) y\(\angle c\).
El ángulo de\(70^{\circ}\) es adyacente\(\angle c\) y los dos ángulos forman un ángulo recto.
A continuación, expresar la relación usando símbolos.
\(\angle c+70^{\circ}=180^{\circ}\)
A continuación, restar\(70^{\circ}\) de ambos lados de la ecuación.
\(\angle c+70^{\circ}=180^{\circ}\)
\(\angle c+70^{\circ}-70^{\circ}=180^{\circ} -70^{\circ}\)
Entonces, simplifique ambos lados de la ecuación.
\(\angle c+70^{\circ}-70^{\circ}=180^{\circ} -70^{\circ}\)
\(\angle c=110^{\circ}\)
La respuesta es\(110^{\circ}\).
\(m \angle c=110^{\circ}\)
Ejemplo\(\PageIndex{1}\)
Antes, se le dio un problema sobre el campo de béisbol y las líneas de falta.
El ángulo entre la trayectoria de la pelota y la línea de falta de primera base necesita ser resuelto. Esto se puede hacer usando ángulos complementarios.
Solución
Primero, dibuje un diagrama para modelar el problema.
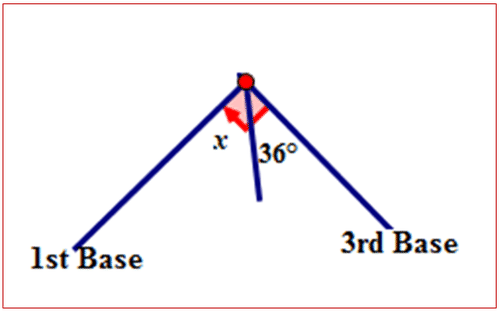Figura\(\PageIndex{8}\)A continuación, exponer la relación entre\(36^{\circ}\) y\(\angle x\).
\(36^{\circ}\)y\(\angle x\) son ángulos complementarios. La suma de los ángulos es\(90^{\circ}\).
A continuación, expresar la relación usando símbolos.
\(36^{\circ}+\angle x=90^{\circ}\)
A continuación, restar 36° de ambos lados de la ecuación.
\(36^{\circ}+\angle x=90^{\circ}\)
\(36^{\circ}-36^{\circ}+\angle x=90^{\circ}-36^{\circ}\)
Entonces, simplifique ambos lados de la ecuación.
\(36^{\circ}-36^{\circ}+\angle x=90^{\circ}-36^{\circ}\)
\(\angle x = 54^{\circ}\)
La respuesta es\(54^{\circ}\).
\(54^{\circ}\)Se hace un ángulo de entre la línea de falta de primera base y el camino del beisbol.
Ejemplo\(\PageIndex{2}\)
Si los siguientes ángulos son complementarios, encuentra la medida del ángulo faltante.
\(\angle A=37^{\circ}\)entonces\(\angle B=\)?
Solución
Primero, dibuje un diagrama para modelar el problema.
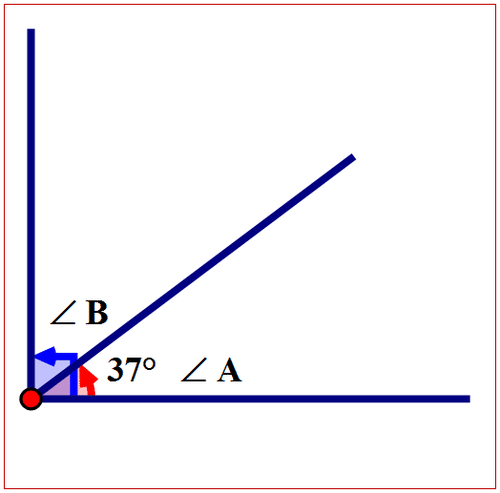Figura\(\PageIndex{9}\)A continuación, exponer la relación entre\(\angle A\) y\(\angle B\).
\(\angle A\)y\(\angle B\) son ángulos complementarios. La suma de los ángulos es\(90^{\circ}\).
A continuación, expresar la relación usando símbolos.
\(\angle A+ \angle B=90^{\circ}\)
A continuación, sustituya la medida de\(\angle A\) en la ecuación.
\(37^{\circ}+ \angle B=90^{\circ}\)
A continuación, restar\(37^{\circ}\) de ambos lados de la ecuación.
\(37^{\circ}+ \angle B=90^{\circ}\)
\(37^{\circ}- 37^{\circ}+ \angle B=90^{\circ}- 37^{\circ}\)
Entonces, simplifique ambos lados de la ecuación.
\(37^{\circ}- 37^{\circ}+ \angle B=90^{\circ}- 37^{\circ}\)
\(\angle B =53^{\circ}\)
La respuesta es\(53^{\circ}\).
\(m \angle B =53^{\circ}\)
Ejemplo\(\PageIndex{3}\)
Si los siguientes ángulos son complementarios, encuentre la medida del ángulo faltante.
\(\angle A=102^{\circ}\)entonces\(\angle B=\)?
Solución
Primero, dibuje un diagrama para modelar el problema.
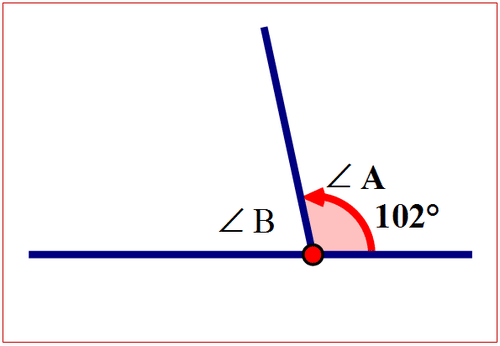Figura\(\PageIndex{10}\)A continuación, exponer la relación entre\(\angle A\) y\(\angle B\).
\(\angle A\)y\(\angle B\) son ángulos suplementarios. La suma de los ángulos es de 180°.
A continuación, expresar la relación usando símbolos.
\(\angle A+ \angle B=180^{\circ}\)
A continuación, sustituya la medida de\(\angle A\) en la ecuación.
\(102^{\circ}+\angle B=180^{\circ}\)
A continuación, restar\(102^{\circ}\) de ambos lados de la ecuación.
\(102^{\circ}+\angle B=180^{\circ}\)
\(102^{\circ}-102^{\circ}+\angle B=180^{\circ}-102^{\circ}\)
Entonces, simplifique ambos lados de la ecuación.
\(102^{\circ}-102^{\circ}+\angle B=180^{\circ}-102^{\circ}\)
\(\angle B=78^{\circ}\)
La respuesta es\(78^{\circ}\).
\(m \angle B=78^{\circ}\)
Ejemplo\(\PageIndex{4}\)
Usando el siguiente diagrama, determine las medidas de los ángulos faltantes.
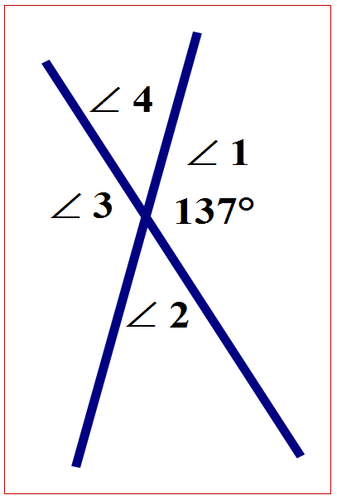Figura\(\PageIndex{11}\)Solución
Primero, exponer la relación entre el ángulo de\(\angle 1\) y\(\angle 3\).
\(\angle 1\)y\(\angle 3\) son ángulos verticales y son iguales en medida.
A continuación, expresar la relación usando símbolos.
\(m\angle 1=m \angle 3\)
A continuación, sustituya la medida de\(\angle 1\) en la ecuación.
\(m\angle 1=m \angle 3\)
\(137^{\circ}=m\angle 3\)
La respuesta es\(137^{\circ}\).
\(m\angle 3= 137^{\circ}\)
Primero, exponer la relación entre el ángulo de\(\angle 1\) y\(\angle 2\).
\(\angle 1\)es adyacente\(\angle 2\) y los dos ángulos forman un ángulo recto.
A continuación, expresar la relación usando símbolos.
\(\angle 1+\angle 2=180^{\circ}\)
A continuación, sustituya la medida de\(\angle 1\) en la ecuación.
\(137^{\circ}+\angle 2=180^{\circ}\)
A continuación, restar\(137^{\circ}\) de ambos lados de la ecuación.
\(137^{\circ}+\angle 2=180^{\circ}\)
\(137^{\circ}-137^{\circ}+\angle 2=180^{\circ}-137^{\circ}\)
Entonces, simplifique ambos lados de la ecuación.
\(137^{\circ}-137^{\circ}+\angle 2=180^{\circ}-137^{\circ}\)
\(\angle 2=43^{\circ}\)
La respuesta es\(43^{\circ}\).
\(m \angle 2=43^{\circ}\)
Primero, exponer la relación entre el ángulo de\(\angle 2\) y\(\angle 4\).
\(\angle 2\)y\(\angle 4\) son ángulos verticales y son iguales en medida.
A continuación, expresar la relación usando símbolos.
\(m \angle 2=m \angle 4\)
A continuación, sustituya la medida de\(\angle 2\) en la ecuación.
\(m \angle 2=m \angle 4\)
\(43^{\circ}=m \angle 4\)
La respuesta es\(43^{\circ}\).
\(m \angle 4=43^{\circ}\)
Revisar
Si los siguientes pares de ángulos son complementarios, entonces ¿cuál es la medida del ángulo faltante?
1. ¿Si\(\angle A=45^{\circ}\) entonces\(\angle B=\)?
2. ¿Si\(\angle C=83^{\circ}\) entonces\(\angle D=\)?
3. ¿Si\(\angle E=33^{\circ}\) entonces\(\angle F=\)?
4. ¿Si\(\angle G=53^{\circ}\) entonces\(\angle H=\)?
Si los siguientes pares de ángulos son complementarios, ¿cuál es la medida del ángulo faltante?
5. ¿Si\(\angle A=40^{\circ}\) entonces\(\angle B=\)?
6. ¿Si\(\angle A=75^{\circ}\) entonces\(\angle B=\)?
7. ¿Si\(\angle C=110^{\circ}\) entonces\(\angle F=\)?
8. ¿Si\(\angle D=125^{\circ}\) entonces\(\angle E=\)?
9. ¿Si\(\angle M=10^{\circ}\) entonces\(\angle N=\)?
10. ¿Si\(\angle O=157^{\circ}\) entonces\(\angle P=\)?
Defina los siguientes tipos de pares de ángulos.
11. Ángulos verticales
12. Ángulos adyacentes
13. Ángulos complementarios
14. Ángulos suplementarios
15. Ángulos interiores
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.4.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulos adyacentes | Dos ángulos son adyacentes si comparten un lado y un vértice. La palabra 'adyacente' significa 'al lado' o 'al lado de'. |
| Ángulo | Una figura geométrica formada por dos rayos que conectan en un solo punto o vértice. |
| Líneas de intersección | Las líneas que se cruzan son líneas que se cruzan o se encuentran en algún momento. |
| Paralelo | Dos o más líneas son paralelas cuando se encuentran en el mismo plano y nunca se cruzan. Estas líneas siempre tendrán la misma pendiente. |
| Líneas perpendiculares | Las líneas perpendiculares son líneas que se cruzan en\(90^{\circ}\) ángulo. |
| Ángulo recto | Un ángulo recto es una línea recta igual a\(180^{\circ}\). |
Recursos adicionales
Elemento Interactivo
Video: Ángulos complementarios, suplementarios y verticales
Practica:Propiedades de ángulo y teoremas