5.15: Área de Paralelogramos- Cuadrados, Rectángulos y Trapezoides
- Page ID
- 107534
Encuentra el área de rectángulos, paralelogramos, trapezoides.
Encuentra las dimensiones y el área de cuadriláteros
Montgomery Middle School va a ser sede de una Olimpiada en toda la escuela por primera vez. Ya comenzaron los preparativos iniciales y en seis semanas se llevará a cabo un fantástico evento olímpico de dos días. La clase de la señora Meery estará construyendo la plataforma para la ceremonia de entrega de premios. La plataforma es en forma de trapecio con bases de 35 pies y 41 pies y una altura de 7.5 pies. Si una cubeta de cemento cubre 25 pies cuadrados, ¿cuántos cubos necesitarán los estudiantes para construir la plataforma?
En este concepto, aprenderás a encontrar las dimensiones y áreas de diferentes cuadriláteros.
Cuadriláteros
Los cuadriláteros son polígonos de cuatro lados. Se clasifican por las características de sus lados y ángulos. Rectángulos, cuadrados, paralelogramos, rombos y trapecios son todos cuadriláteros. Las siguientes imágenes muestran algunos de los cuadriláteros y sus características.




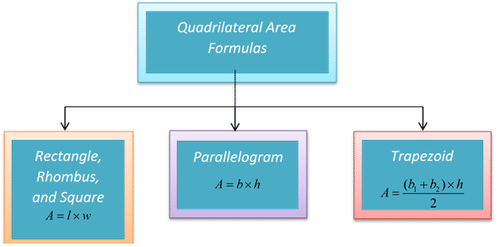
Cada uno de estos cuadriláteros tiene su propia fórmula de área.
Veamos un ejemplo.
¿Cuál es el área de un rectángulo con una longitud de 6 pulgadas y un ancho de 4 pulgadas?
Primero, rellena lo que sabes en la fórmula para el área de un rectángulo.
\(\begin{aligned} A&=l\times w \\ A&=6\times 4 \end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned}A&=6\times 4 \\ A&=24\end{aligned}\)
La respuesta es 24.
El área del rectángulo es\(24\text{ in }^2\), o 24 pulgadas cuadradas.
Veamos otro ejemplo.
¿Cuál es el área del paralelogramo a continuación?
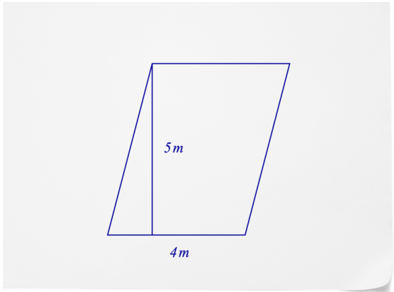
Primero, sustituya lo que sabes en la fórmula por el área de un paralelogramo.
\(\begin{aligned} A&=b\times h \\ A&=4\times 5\end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned}A&=4\times 5 \\ A&=20\end{aligned}\)
La respuesta es 20.
El área del paralelogramo es\(20\text{ m}^2\), o 20 metros cuadrados.
Veamos un ejemplo más.
Encuentra el área del trapecio a continuación.
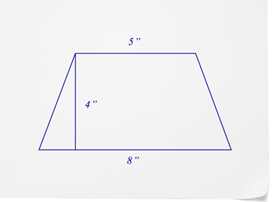
Primero, sustituya lo que sabes en la fórmula por el área de un trapecio.
\(\begin{aligned} A&=\dfrac{(b_1+b_2)\times h}{2} \\ A&=\dfrac{(5+8)\times 4}{2} \end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned} A&=\dfrac{(5+8)\times 4}{2} \\ A&=26 \end{aligned}\)
La respuesta es 26.
El área del trapecio es\(26\text{ in }^2\), o 26 pulgadas cuadradas.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre el podio de la escuela.
El podio es en forma de trapecio que tiene medidas de base de 35 pies y 41 pies y una altura de 7.5 pies. El podio está siendo hecho de cemento donde una cubeta de cemento cubre 25 pies cuadrados. Es necesario encontrar el área del podio y luego el número de cubetas de cemento para hacerlo.
Solución
Primero, sustituya lo que sabes en la fórmula por el área de un trapecio.
\(\begin{aligned} A&=\dfrac{(b_1+b_2)\times h}{2} \\ A&=\dfrac{(35+41)\times 7.5}{2} \end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned}A&=\dfrac{(35+41)\times 7.5}{2} \\ A&=285 \end{aligned}\)
Después, divida el área por 25 para determinar el número de cubetas de cemento a utilizar.
\(\text{ # of buckets}=\dfrac{285}{25}\)
\(\text{ # of buckets}=11.4\)
La respuesta es 11.4.
Los alumnos tendrán que comprar 12 cubetas de cemento para su proyecto.
Ejemplo\(\PageIndex{2}\)
Un paralelogramo tiene un área de\(105\: m^2\). La altura del paralelogramo es de 7 m. ¿Cuál es su base?
Solución
Primero, sustituya lo que sabes en la fórmula por el área de un paralelogramo.
\(\begin{aligned} A&=b\times h \\ 105&=b\times 7\end{aligned}\)
A continuación, divide ambos lados por 7 para resolver\(b\).
\(\begin{aligned} 105&=b\times 7 \\ \dfrac{105}{7}&=\dfrac{7b}{7} \\ b&=15\end{aligned}\)
La respuesta es 15.
La base del paralelogramo tiene una longitud de 15 m.
Ejemplo\(\PageIndex{3}\)
¿Cuál es el área de un cuadrado con una longitud lateral de 4.5 pulgadas?
Solución
Primero, sustituya lo que sabes en la fórmula por el área de un cuadrado.
\(\begin{aligned} A&=l\times w \\ A&=4.5\times 4.5\end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned} A&=4.5\times 4.5 \\ A&=20.25 \end{aligned}\)
La respuesta es 20.25. Por lo tanto, el área del cuadrado es\(20.25 \text{ in}^2\), o 20.25 pulgadas cuadradas.
Ejemplo\(\PageIndex{4}\)
¿Cuál es el área de un rectángulo con una longitud de 8 pies y un ancho de 6.25 pies?
Solución
Primero, sustituya lo que sabes en la fórmula por el área de un rectángulo.
\(\begin{aligned} A&=l\times w \\ A&=8\times 6.25 \end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned} A&=8\times 6.25 \\ A&=50 \end{aligned} \)
La respuesta es 50.
El área del rectángulo es 50 ft^2\), o 50 pies cuadrados.
Ejemplo\(\PageIndex{5}\)
¿Cuál es el área de un paralelogramo con una base de 10 metros y una altura de 7.5 metros?
Solución
Primero, sustituya lo que sabes en la fórmula por el área de un paralelogramo.
\(\begin{aligned} A&=b\times h \\ A&=10\times 7.5 \end{aligned}\)
A continuación, resolver para\(A\).
\(\begin{aligned} A&=10\times 7.5 \\ A&=75 \end{aligned}\)
La respuesta es 75.
El área del paralelogramo es de 75 m2, o 75 metros cuadrados.
Revisar
1. \(l=10\text{ in },\: w=7.5\text{ in }\)
2. \(l=12\text{ ft },\: w=9\text{ ft }\)
3. \(l=14\text{ ft },\: w=11\text{ ft }\)
4. \(l=21\text{ ft },\: w=19\text{ ft }\)
Encuentra el área de cada paralelogramo.
5. \(b=11\text{ ft },\: h=9\text{ ft }\)
6. \(b=13\text{ in },\: h=11\text{ in }\)
7. \(b=22\text{ ft },\: h=19\text{ ft }\)
8. \(b=31\text{ meters },\: h=27\text{ meters }\)
Encuentra el área de cada trapecio.
9. \(Bases=5\text{ in } \:and \:8 in,\: height=4 \text{ inches }\)
10. \(Bases=6 \:in \:and \:8\text{ in },\: height=5 \text{ inches }\)
11. \(Bases=10\text{ feet }\: and\: 12\text{ feet },\: height=9\text{ feet }\)
Encuentra el área de cada plaza.
12. longitud lateral de 8 pulgadas
13. longitud lateral de 15 pies
14. longitud lateral de 22.5 mm
15. largo lateral de 18.25 cm
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.2.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Perperpendicular | Las líneas perpendiculares son líneas que se cruzan en\(90^{\circ}\) ángulo. El producto de las pendientes de dos líneas perpendiculares es -1. |
| Polígono | Un polígono es una simple figura cerrada con al menos tres lados rectos. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
Recursos adicionales
Elemento interactivo
Video: Determinar el área de un rectángulo que involucra números enteros
Práctica: Área de Paralelogramos: Cuadrados, Rectángulos y Trapezoides

