6.12: Acordes y arcos de ángulo central
- Page ID
- 107261
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Arcos determinados por ángulos cuyo vértice es el centro de un círculo y acordes (segmentos que conectan dos puntos en un círculo).
Acordes en Círculos
Teoremas de Acorde
Existen varios teoremas importantes sobre acordes que te ayudarán a analizar mejor los círculos.
1. Teorema de Acorde #1: En el mismo círculo o círculos congruentes, los arcos menores son congruentes si y sólo si sus acordes correspondientes son congruentes.
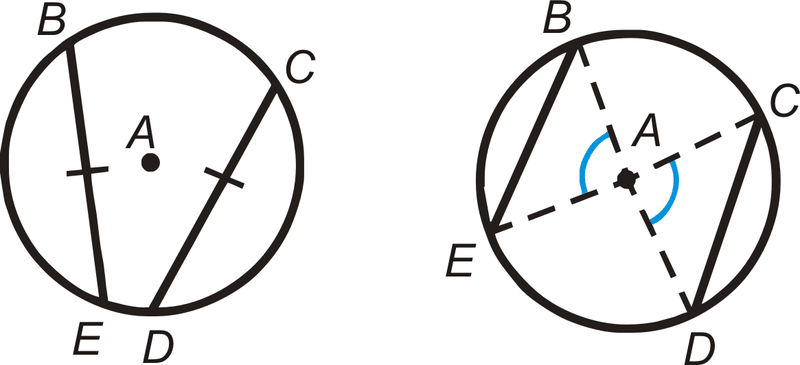
En ambas fotos,\(\overline{BE}\cong \overline{CD}\) y\(\widehat{BE}\cong \widehat{CD}\).
2. Teorema de Acorde #2: La bisectriz perpendicular de una cuerda también es un diámetro.
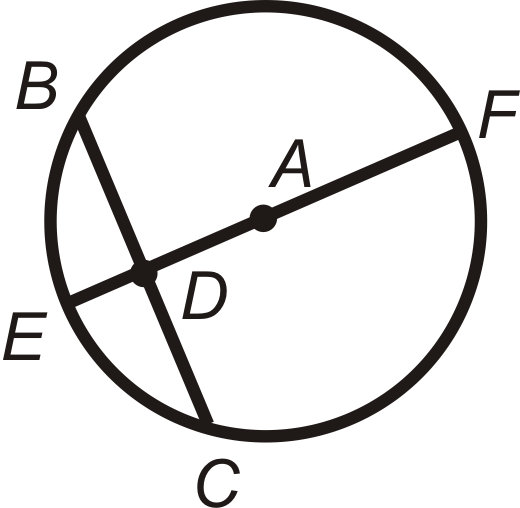
Si\(\overline{AD}\perp \overline{BC}\) y\(\overline{BD}\cong \overline{DC}\) entonces\(\overline{EF}\) es un diámetro.
3. Teorema de Acorde #3: Si un diámetro es perpendicular a una cuerda, entonces el diámetro biseca la cuerda y su arco correspondiente.
Si\(\overline{EF}\perp \overline{BC}\), entonces\(\overline{BD}\cong \overline{DC}\)
4. Teorema del acorde #4: En el mismo círculo o círculos congruentes, dos acordes son congruentes si y sólo si son equidistantes del centro.
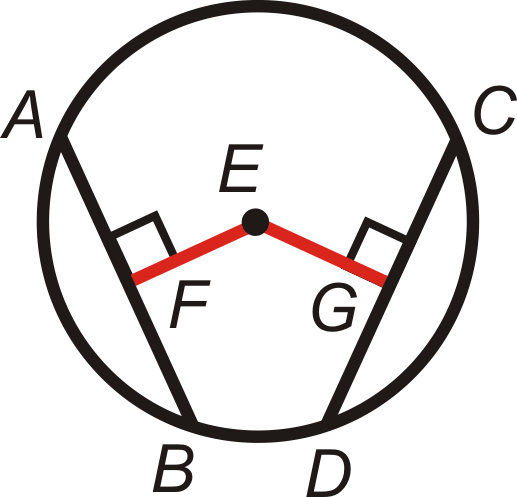
La distancia más corta de cualquier punto a una línea es la línea perpendicular entre ellos. Si\(FE=EG\) y\(\overline{EF}\perp \overline{EG}\), entonces\(\overline{AB}\) y\(\overline{CD}\) son equidistantes al centro y\(\overline{AB}\cong \overline{CD}\).
¿Y si te dieran un círculo con dos acordes dibujados a través de él? ¿Cómo podrías determinar si estos dos acordes eran congruentes?
Ejemplo\(\PageIndex{1}\)
Encuentra el valor de\(x\) y\(y\).
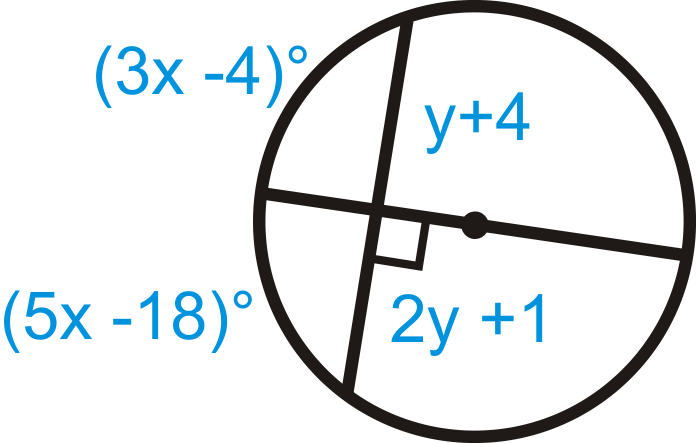
Solución
El diámetro es perpendicular a la cuerda, lo que significa que biseca la cuerda y el arco. Configure ecuaciones para\(x\) y\(y\).
\ (\ begin {array} {rlr}
(3 x-4) ^ {\ circ} & =( 5 x-18) ^ {\ circ} & y+4=2 y+1\\
14 & =2 x & 3=y\\
7 & =x
\ end {array}\)
Ejemplo\(\PageIndex{2}\)
\(BD=12\)y\(AC=3\) en\(\bigodot A\). Encuentra el radio.
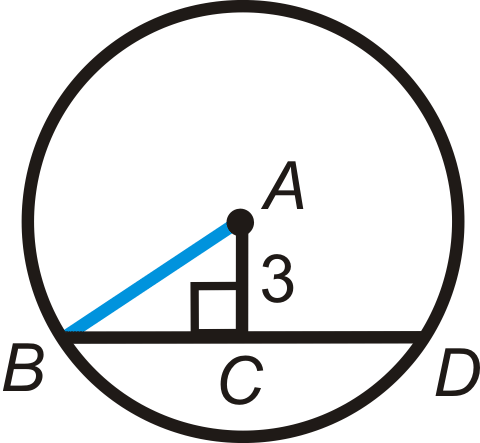
Solución
Primero encuentra el radio. \(\overline{AB}\)es un radio, así podemos usar el triángulo rectángulo\ Delta ABC\) con hipotenusa\(\overline{AB}\). Del Teorema del Acorde #3,\(BC=6\).
\(\begin{aligned} 3^2+6^2&=AB^2 \\ 9+36&=AB^2 \\ AB&=\sqrt{45}=3\sqrt{5}\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
\(\bigodot A\)Utilízala para responder lo siguiente.
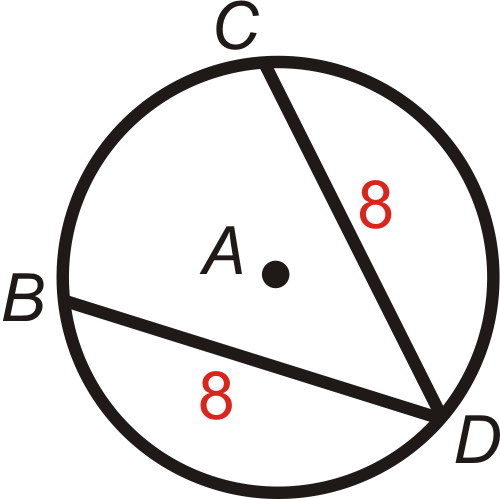
- Si\(m\widehat{BD}=125^{\circ}\), encuentra\(m\widehat{CD}\).
- Si\(m\widehat{BC}=80^{\circ}\), encuentra\(m\widehat{CD}\).
Solución
- \(BD=CD\), lo que significa que los arcos también son congruentes. \(m\widehat{CD}=125^{\circ}\).
- \(m\widehat{CD}\cong m\widehat{BD}\)porque\(BD=CD\).
\(\begin{aligned} m\widehat{BC}+m\widehat{CD}+m\widehat{BD}&=360^{\circ} \\ 80^{\circ}+2m\widehat{CD}&=360^{\circ} \\ 2m\widehat{CD}&=280^{\circ} \\ m\widehat{CD}=140^{\circ}\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Encuentra los valores de\(x\) y\(y\).
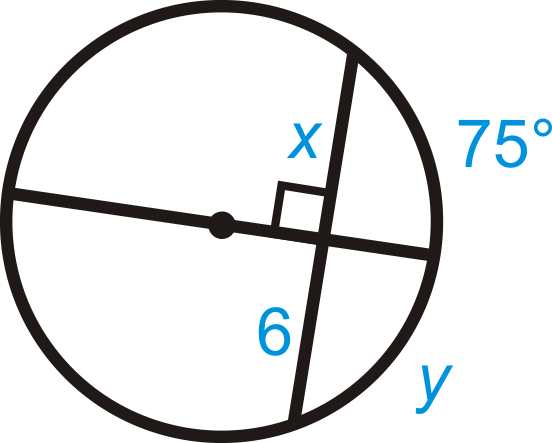
Solución
El diámetro es perpendicular a la cuerda. Del Teorema de Acorde #3,\(x=6\) y\(y=75^{\circ}\).
Ejemplo\(\PageIndex{5}\)
Encuentra el valor de\(x\).
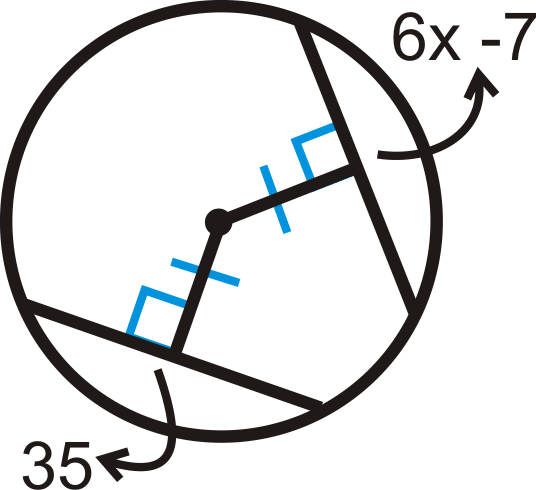
Solución
Debido a que la distancia desde el centro a los acordes es igual, los acordes son congruentes.
\(\begin{aligned} 6x−7&=35 \\ 6x&=42 \\ x&=7 \end{aligned}\)
Revisar
Rellene los espacios en blanco.
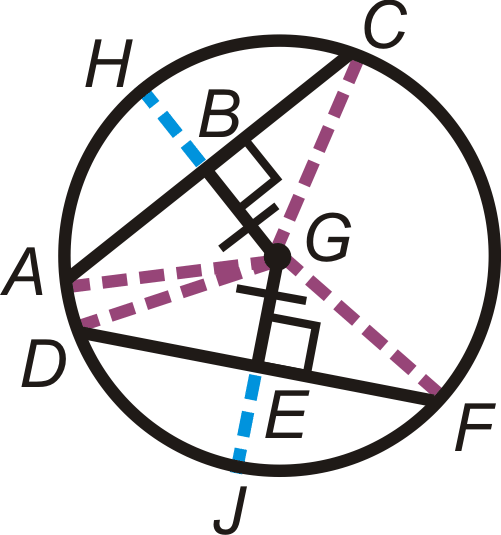
- \(\text{_____}\cong \overline{DF}\)
- \(\widehat{AC} \cong \text{_____}\)
- \(\widehat{DJ}\cong \text{_____}\)
- \(\text{_____}\cong \overline{EJ}\)
- \(\angle AGH\cong \text{_____}\)
- \(\angle DGF\cong \text{_____}\)
- Enumere todos los radios congruentes en\(\bigodot G\).
Encuentra el valor del arco indicado en\(\bigodot A\).
- \(m\widehat{BC}\)
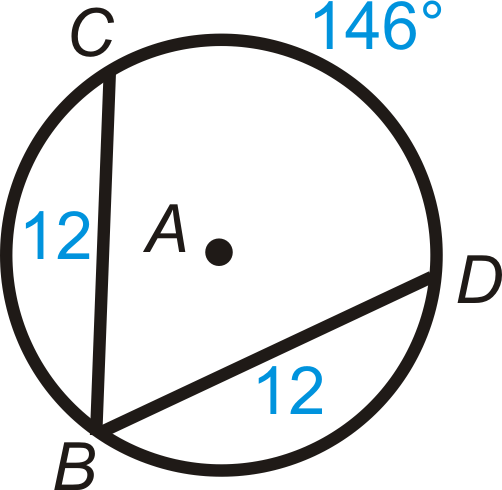
Figura\(\PageIndex{11}\) - \(m\widehat{BD}\)
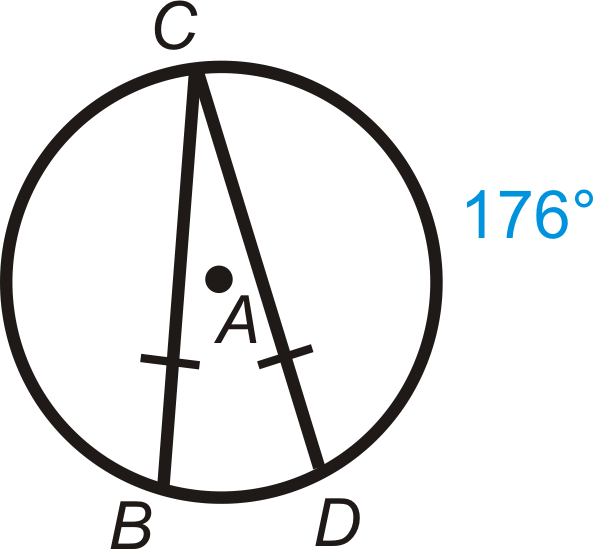
Figura\(\PageIndex{12}\) - \(m\widehat{BC}\)
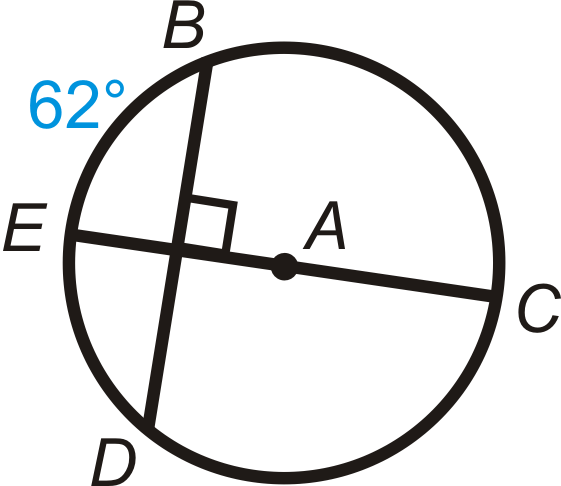
Figura\(\PageIndex{13}\) - \(m\widehat{BD}\)
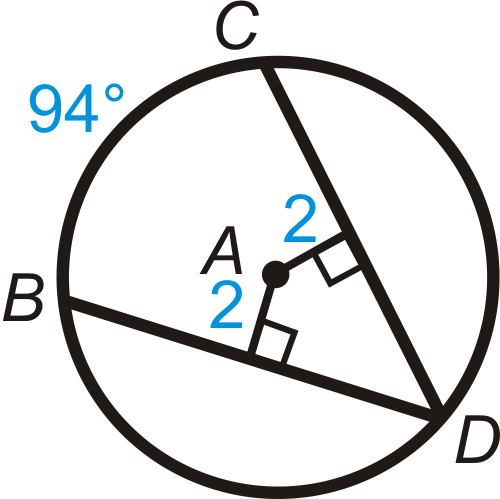
Figura\(\PageIndex{14}\) - \(m\widehat{BD} \)
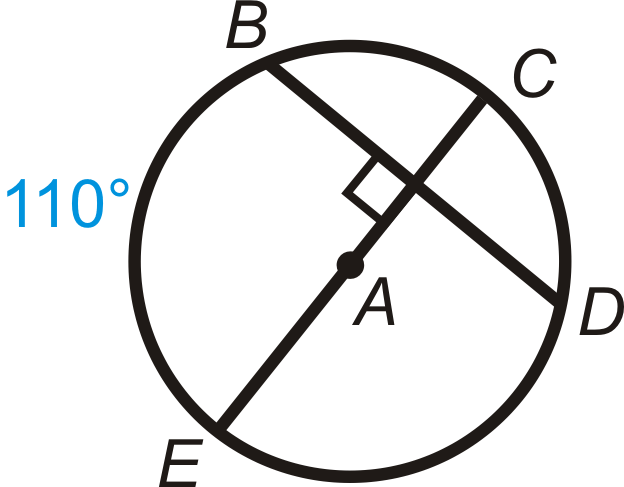
Figura\(\PageIndex{15}\) - \(m\widehat{BD}\)
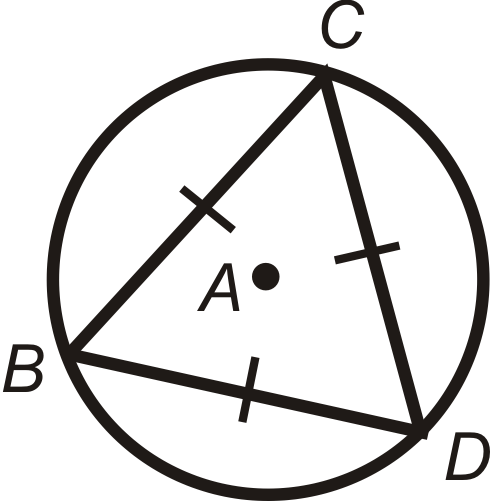
Figura\(\PageIndex{16}\)
Encuentra el valor de\(x\) y/o\(y\).
-
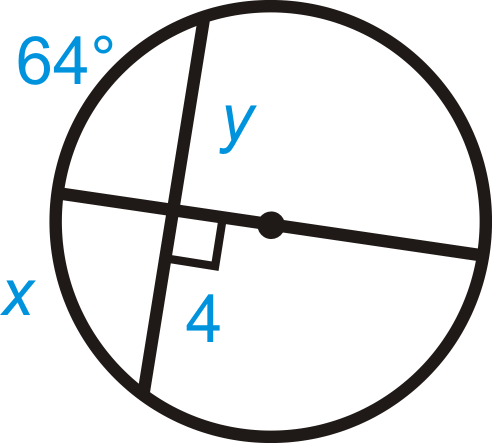
Figura\(\PageIndex{17}\) -
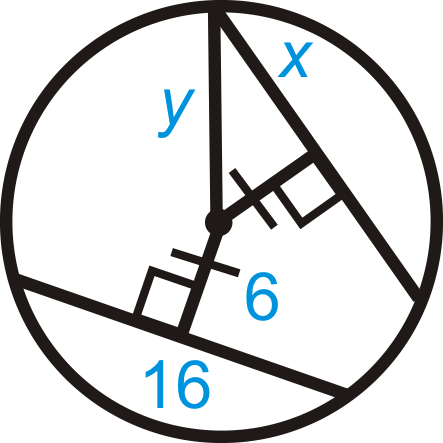
Figura\(\PageIndex{18}\) -
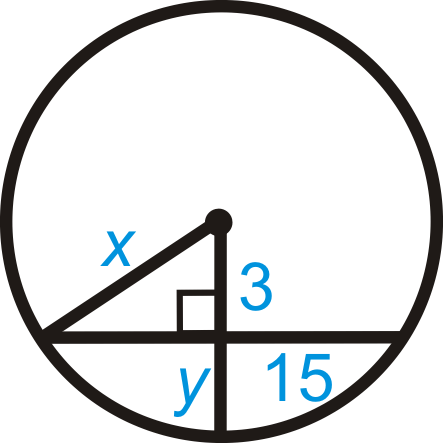
Figura\(\PageIndex{19}\) - \(AB=32\)
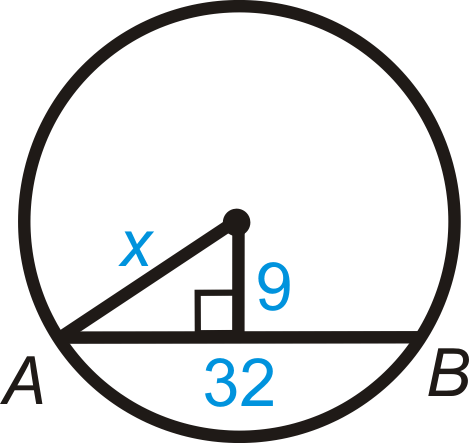
Figura\(\PageIndex{20}\) -
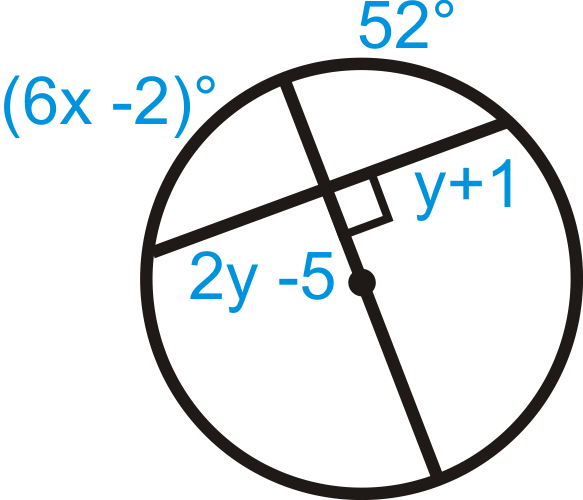
Figura\(\PageIndex{21}\) -
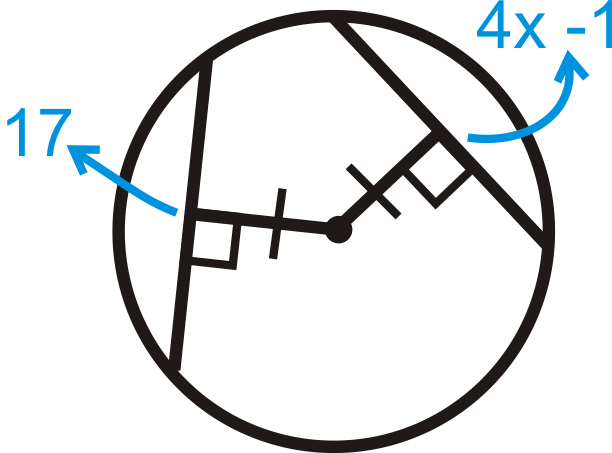
Figura\(\PageIndex{22}\) -
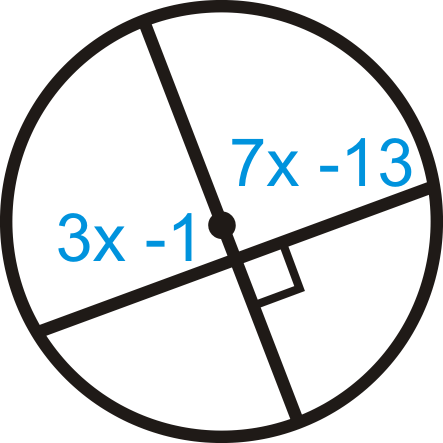
Figura\(\PageIndex{23}\) -
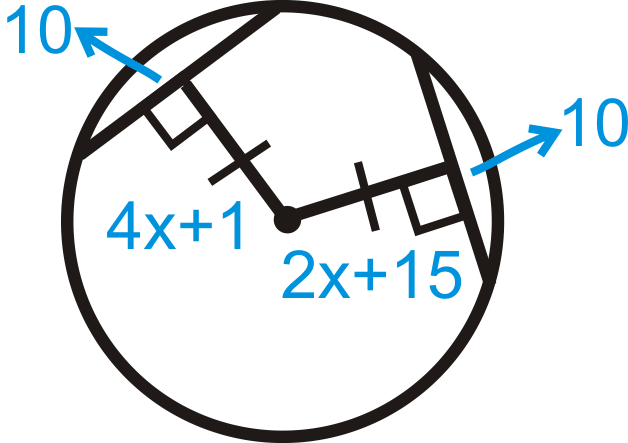
Figura\(\PageIndex{24}\) - \(AB=20\)
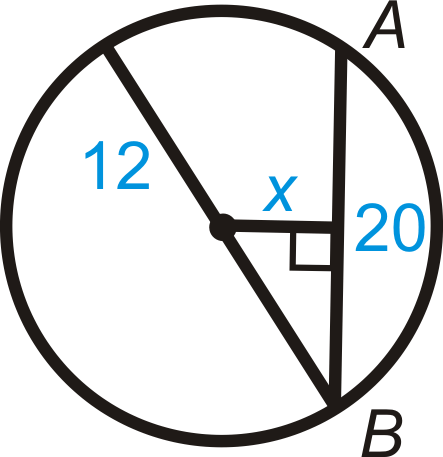
Figura\(\PageIndex{25}\) - Encuentra\(m\widehat{AB}\) en la Pregunta 17. Redondea tu respuesta al décimo de grado más cercano.
- Encuentra\(m\widehat{AB}\) en la Pregunta 22. Redondea tu respuesta al décimo de grado más cercano.
En los problemas 25-27, ¿qué se puede concluir sobre el panorama? Afirma un teorema que justifique tu respuesta. Se puede suponer que A es el centro del círculo.
-
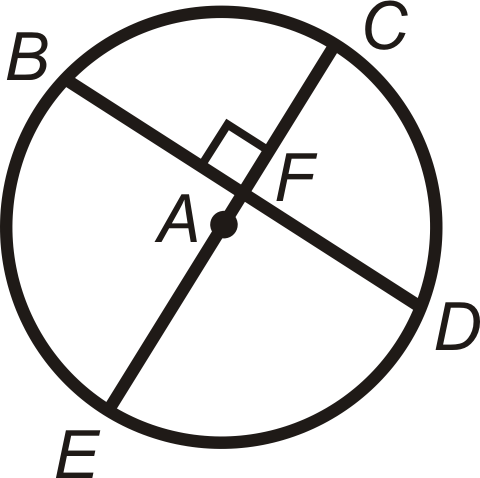
Figura\(\PageIndex{26}\) -
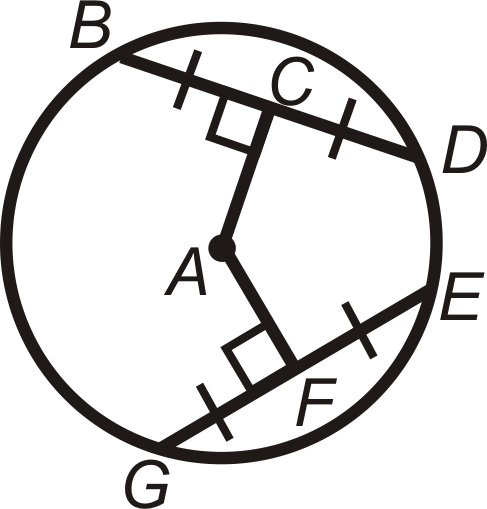
Figura\(\PageIndex{27}\) -
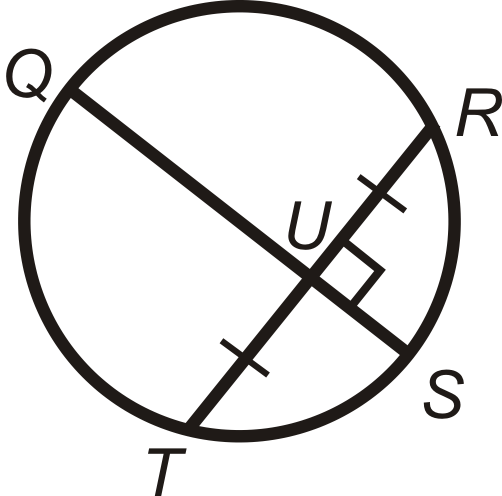
Figura\(\PageIndex{28}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.4.
El vocabulario
| Término | Definición |
|---|---|
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
Recursos adicionales
Elemento Interactivo
Video: Acordes en Círculos Principios - Básico
Actividades: Acordes en Círculos Preguntas de Discusión
Ayudas de estudio: Círculos: segmentos y longitudes Guía de estudio
Práctica: Acordes y arcos de ángulo central