8.1: Identificar tipos de transformación

Identificar transformaciones, traducciones, reflexiones y rotaciones.

Transformaciones en el Plano

La transformación es un proceso que cambia la forma, tamaño o posición de una figura para crear una nueva imagen. Es una función que toma puntos en el plano como entradas y da otros puntos como salidas. Puedes pensar en una transformación como una regla que te diga cómo crear nuevos puntos.

Supongamos que tiene una transformación\(F\) que aplica un factor de estiramiento horizontal de dos a cada punto. A continuación, esta transformación se aplica al triángulo\(S\) para crear triángulo\(S'\).

• \(S'\)se considera la imagen de\(S\) por\(F\).
• También es correcto decir que los\(F\) mapas\(S\) a\(S'\).
• Cada uno de los puntos de la imagen está etiquetado con un símbolo ′, que se lee como “primo”.

Esto ayuda a mostrar cómo los puntos en\(S\) corresponden a los puntos en\(S'\). Por ejemplo, se podría decir que “el punto A mapea al punto A-prime”.

Figura\(\PageIndex{1}\)

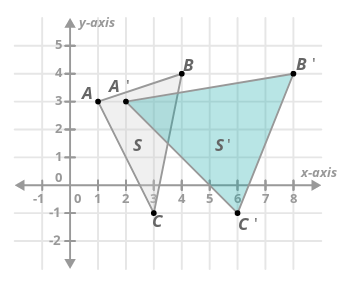
Algunas transformaciones conservan la longitud y los ángulos. Preservar la longitud significa que si un segmento de línea es de 3 unidades, su imagen también será de 3 unidades. De igual manera, preservar los ángulos significa que si un ángulo es\(60^{\circ}\), su imagen también lo será\(60^{\circ}\).

• Una transformación que preserva la longitud y los ángulos se denomina transformación rígida.

Reconocer Transformaciones Rígidas

1. ¿Es un estiramiento horizontal un ejemplo de una transformación rígida?

Figura\(\PageIndex{2}\)

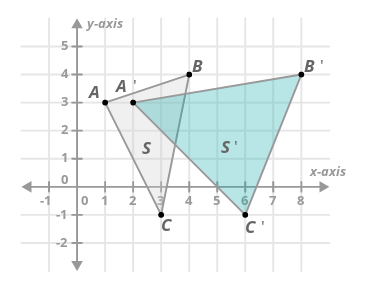
No. Puedes demostrarlo usando la imagen de arriba mostrando que la longitud no se conserva.

Figura\(\PageIndex{3}\)

Figura\(\PageIndex{4}\)

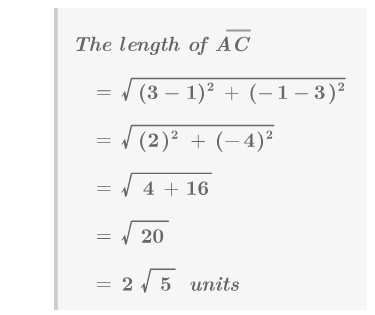
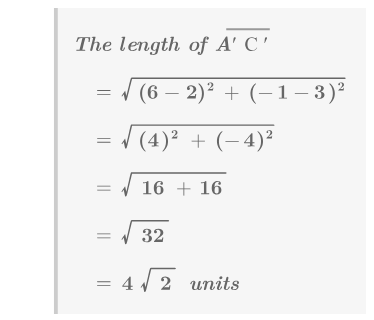
2. Una transformación refleja puntos en forma\(\overleftrightarrow{AB}\) a\(K\) través para crear forma\(K′\). ¿Es esta reflexión una transformación rígida?

Figura\(\PageIndex{5}\)

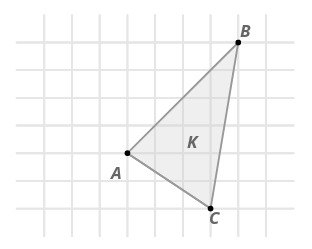
Sí, las reflexiones son transformaciones rígidas. Se puede verificar que se conservan las distancias entre los puntos.

3. Una transformación traduce puntos en forma\(K\) a lo largo del vector\(\rightarrow{v}\) para crear forma\(K′\). ¿Es esta traducción una transformación rígida?

Figura\(\PageIndex{6}\)

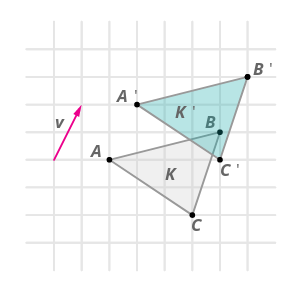
Sí, las traducciones son transformaciones rígidas. Se puede verificar que se conservan las distancias entre los puntos.

Elemento Interactivo

Agrega el texto del elemento interactivo aquí. Esta caja NO se imprimirá en pdf

Ejemplo\(\PageIndex{1}\)

Deslizas un libro por tu escritorio. Viertes refresco de una lata en un vaso grande. Describir estas acciones como transformaciones.

Solución

Deslizar un libro por tu escritorio es una transformación rígida porque un libro es un objeto rígido que no cambia de forma. Las distancias y ángulos que componen el libro no cambian una vez que el libro está en una nueva ubicación. Verter refresco, por otro lado, no es una transformación rígida. El líquido no es un objeto rígido y puede cambiar de forma dependiendo de su entorno. La forma general de la soda en la lata será diferente de la forma general de la soda en el vaso.

Ejemplo\(\PageIndex{2}\)

Una transformación gira los puntos de forma\(K\) alrededor del punto\(D\) para crear la forma\(K′\). ¿Esta rotación parece una transformación rígida? Usa álgebra para probar tu respuesta.

Figura\(\PageIndex{7}\)

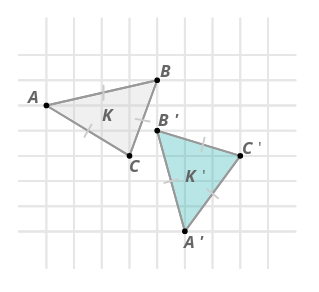
Solución

Esto parece ser una transformación rígida.

Con el Teorema de Pitágoras, se puede demostrar que los lados correspondientes son de la misma longitud. Por ejemplo:

\(\begin{aligned} \text{ The length of } \overline{AC} \\&=\sqrt{3^2+2^2} \\ &=\sqrt{9+4} \\ &=\sqrt{13}\text{ units } \\ \text{ The length of }\overline{A′C′} \\ &=\sqrt{3^2+2^2} \\ &=\sqrt{9+4} \\ &=\sqrt{13}\text{ units } \end{aligned}\)

Por lo tanto, en efecto, es una transformación rígida.

Ejemplo\(\PageIndex{3}\)

¿Qué hace que una transformación sea una transformación rígida?

Solución

Las transformaciones rígidas conservan la distancia y los ángulos. Todos los lados correspondientes serán de la misma longitud y todos los ángulos correspondientes serán de la misma medida.

Revisar

Para 1-7, defina cada enunciado como verdadero o falso y justifique su respuesta.

1. Las traducciones son transformaciones rígidas.

2. Las rotaciones son transformaciones rígidas.

3. Los estiramientos horizontales son transformaciones rígidas.

4. Las transformaciones rígidas conservan la ubicación en el plano.

5. Los lados correspondientes en transformaciones rígidas tienen la misma longitud.

6. Si no es una transformación rígida, no es una transformación real.

7. Las reflexiones son transformaciones rígidas.

Utilice la siguiente imagen para 8-9.

Figura\(\PageIndex{8}\)

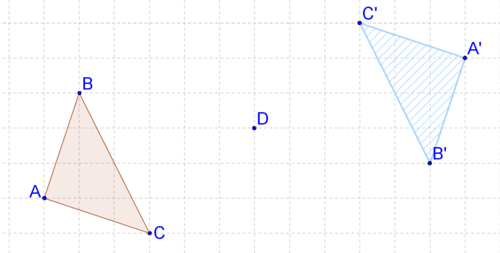
8. Describa la transformación con sus propias palabras. ¿Parece una transformación rígida?

9. Demuestra tu respuesta a #8 comparando las longitudes de dos lados.

Utilice la siguiente imagen para el 10-11.

Figura\(\PageIndex{9}\)

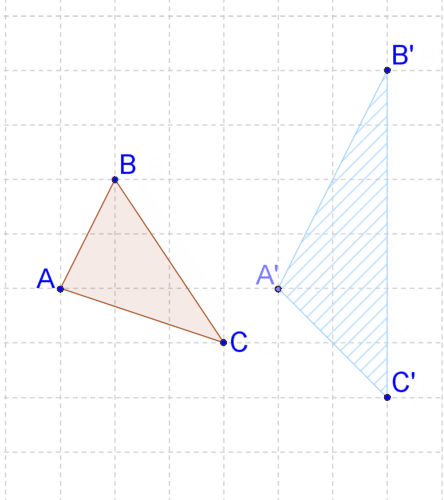
10. Describa la transformación con sus propias palabras. ¿Parece una transformación rígida?

11. Demuestra tu respuesta a #10 comparando las longitudes de dos lados.

Utilice la siguiente imagen para 12-13.

Figura\(\PageIndex{10}\)

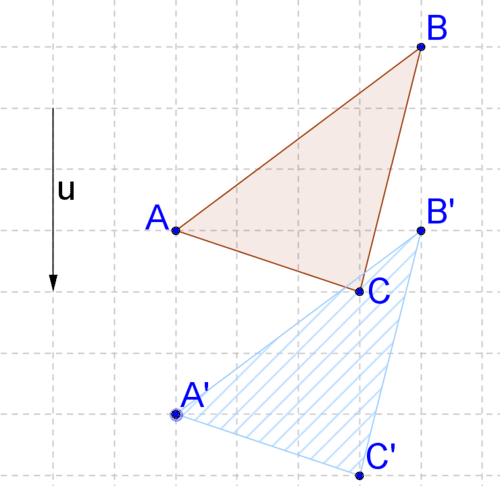
12. Describa la transformación con sus propias palabras. ¿Parece una transformación rígida?

13. Demuestra tu respuesta a #12 comparando las longitudes de dos lados.

Utilice la siguiente imagen para 14-15.

Figura\(\PageIndex{11}\)

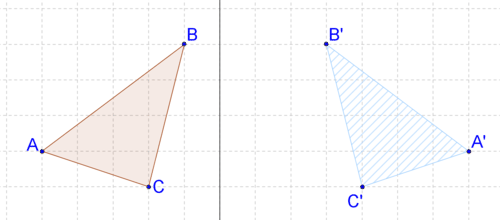
14. Describa la transformación con sus propias palabras. ¿Parece una transformación rígida?

15. Demuestra tu respuesta a #14 comparando las longitudes de dos lados.

16. Una transformación puede pensarse como un movimiento de un objeto en un plano tal que se conservan las medidas de ángulo y las longitudes de los segmentos. Imagina un triángulo que hayas recortado, acostado plano sobre un trozo de papel para póster. ¿Cómo se puede mover el triángulo para que se conserven las medidas de los ángulos y las longitudes de los segmentos? ¿Cómo se pueden categorizar y definir los diferentes tipos de movimientos? Sé creativo. Dibuje, escriba y discuta cómo describir y definir más específicamente los tipos y métodos de transformaciones de movimiento rígido.

17. Hay un tipo de transformación rígida de movimiento que parece requerir que el triángulo descrito anteriormente sea levantado del cartel y volteado. (Matemáticamente, eso no es lo que sucede, sino que se ve así desde nuestra perspectiva tridimensional). ¿Cómo se puede definir y describir esta transformación?

18. A veces podemos describir transformaciones en el plano de coordenadas. Por ejemplo, se pueden alterar específicamente las coordenadas de los vértices de un polígono de acuerdo con una regla. Piensa en cómo puedes modificar las coordenadas de un punto y cuáles serían las consecuencias de cada tipo de modificación. Experimento. Dibuja un polígono en un plano de coordenadas, y altera las coordenadas de acuerdo con diferentes reglas, luego dibuja las imágenes resultantes. Escribe y discute tus conclusiones.

19. Definir y describir las transformaciones que\(A\) mapean\(A'\) a\(A''\) a\(A'''\) continuación.

Figura\(\PageIndex{12}\)

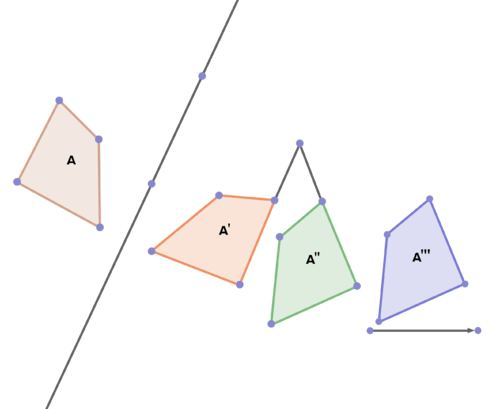
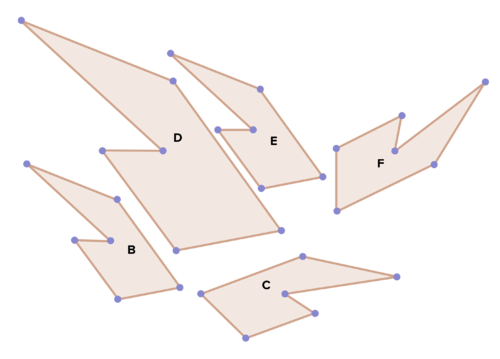
20. Algunas de las siguientes imágenes representan transformaciones rígidas de movimiento del polígono B y otras no. Decide cuál hacer y cuáles no, y explica tus elecciones. Definir y describir los que sí lo hacen.

Figura\(\PageIndex{13}\)

Reseña (Respuestas)

Para ver las respuestas de la opinión, haga clic aquí.

Recursos adicionales

Elemento Interactivo

Práctica: Identificar tipos de transformación