12.3: Coordenadas polares

Última actualización
Guardar como PDF

Page ID: 106674

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las coordenadas cartesianas (\(x,y\)) no son la única manera de etiquetar un punto\(P\) en un plano plano por un par de números. Existen otras formas, y pueden ser más útiles en situaciones especiales.

Un sistema (“coordenadas polares”) utiliza la longitud\(r\) de la línea\(OP\) desde el origen hasta\(P\) (es decir, la distancia de\(P\) distancia al origen) y el ángulo que hace la línea con el eje x. Los ángulos a menudo se denotan con letras griegas, y aquí seguimos convenciones marcándolo con\(\theta\). Tenga en cuenta que mientras en el sistema cartesiano\(x\) y\(y\) juegan papeles muy similares, aquí los roles se dividen:\(r\) da distancia y\(\theta\) dirección.

Las dos representaciones están estrechamente relacionadas. De las definiciones de seno y coseno:

\[x\,=\,r\,\times\, \cos \theta\]

\[y\,=\,r\,\times\, \sin \theta\]

Esto permite\((x,y\)) derivar de coordenadas polares. Esta relación se ilustra a continuación:

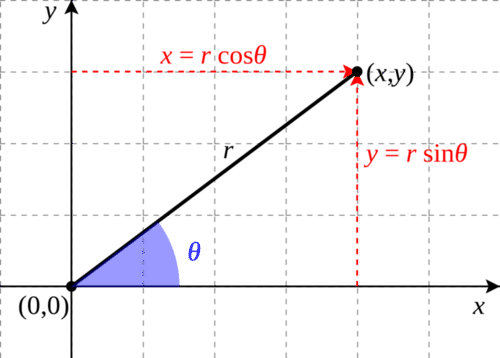
Para ir en sentido inverso, podemos usar el teorema de Pitágoras para encontrar\(r\):

\[r^2\,=\,x^2\,+\,y^2\]

Una vez\(r\) que se conoce, el resto es fácil:

\[\cos \theta\,=\frac{x}{r}\]

\[\sin \theta\,=\frac{y}{r}\]

Estas relaciones fracasan sólo en el origen, donde\(x\,=\,y\,=\,r\,=\,0\). En ese punto,\(\theta\) es indefinido y se puede elegir por ello lo que a uno le plazca.

En el espacio tridimensional, el etiquetado cartesiano (\(x,y,z\)) es muy simétrico, pero a veces es conveniente seguir el estilo de coordenadas polares y etiquetar la distancia y la dirección por separado. La distancia es fácil: se toma la línea OP desde el origen hasta el punto y se mide su longitud r. incluso se puede demostrar desde el teorema de Pitágoras que en este caso

\[r^2\,=\,x^2\,+\,y^2\,+\,z^2\]

Todos los puntos con el mismo valor\(r\) forman una esfera de radio\(r\) alrededor del origen\(O\). En una esfera podemos etiquetar cada punto por latitud\(\lambda\) (lambda, pequeño griego L) y longitud\(\phi\) (phi, pequeño griego F), de manera que la posición de cualquier punto en el espacio se define por los 3 números (\(r,\lambda ,\phi \)).