17.1: Distancia al Horizonte

Última actualización
Guardar como PDF

Page ID: 106772

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Imagina que estabas parado a una altura de\(h\) metros sobre el océano y mirando a través del agua. ¿Cuál es la distancia\(D\) al horizonte? Se puede calcular, si se conoce el radio\(R\) de la Tierra.

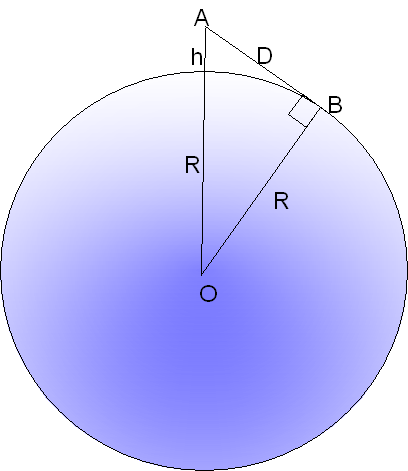
Su línea de visión hacia el horizonte es una tangente a la Tierra —una línea que toca la esfera de la Tierra en un solo punto, marcada\(B\) en el dibujo aquí. Si\(O\) es el centro de la esfera de la Tierra, por un conocido teorema de geometría tal tangente es perpendicular al radio\(OB\), es decir, hace un ángulo de ^90° con ella. Se desprende de aplicar el teorema de Pitágoras a\(\Delta AB\) eso:

\[D^2\,+\,R^2\,=\,(R\,+\,h)^2\]

\[D^2\,=\,(R\,+\,h)^2\,-\,R^2\]

\[D^2\,=\,(R^2\,+\,2Rh)\,+\,h^2\,-\,R^2\]

\[D^2\,=\,2Rh\,+\,h^2\]

\[D^2\,=\,h(2R+h)\]

Dado que el diámetro\(2R\) de la Tierra es mucho mayor que h, podemos reemplazar (\(2R+h)\)por\(2R\) sin afectar significativamente los resultados. Al llevar a cabo este reemplazo se obtiene:

\[D^2\,=\,2Rh\]

\[D\,=\sqrt{2Rh}\]

Esta ecuación permite calcular\(D\) en kilómetros, si\(h\) y\(R\) se dan en kilómetros. También podemos reescribirlo como:

\[D\,=\sqrt{2Rh}\,=\sqrt{2R}\times\sqrt{h}\]

Usando\(R\,=\,6371\) km, encontramos

\[D\,=\,112.88\,km\times\sqrt{h}\]

Si estás parado sobre una montaña a 1 km de altura,\(h=1\) km y tu horizonte debería estar a 112.88 km de distancia (descuidamos la refracción de la luz en la atmósfera, lo que puede modificar este valor). Desde lo alto de Mauna Kea en Hawai, un volcán extinto de unos 4 km de altura (también sitio de importantes observaciones astronómicas), el horizonte debería ser aproximadamente el doble de distante, 226 km. Por otro lado, de pie en la playa con los ojos 2 metros = 0.002 km sobre el agua, ya que\(\sqrt{0.002}\,=\,0.0442\). el horizonte está a sólo 5 km.

El cálculo también debe mantenerse al revés. Desde un barco en el océano deberías comenzar a ver la cima de Mauna Kea después de pasar una distancia de 226 km (nuevamente, sin tener en cuenta la refracción). El 15 de noviembre de 1806, el teniente Zebulon Pike del Ejército de Estados Unidos, al frente de un grupo de exploración a través de las llanuras del medio oeste de Estados Unidos, vio a través de su cristal de cristal la cima de un pico distante, justo por encima del horizonte. Su fiesta tardó una semana en cubrir las 100 millas hasta la montaña, que ahora se conoce como Pico's Peak, una de las más altas de Colorado. Pike en realidad intentó subir a su cima, pero la nieve y la inesperada altura de la montaña lo obligaron a regresar.