1.6: Fórmula de distancia y teorema de Pitágoras

Descubre longitudes de lados triangulares usando el Teorema de Pitágoras. Identificar la distancia como la hipotenusa de un triángulo rectángulo. Determinar la distancia entre pares ordenados.

Teorema de Pitágoras para determinar la distancia

Al caminar un día a la escuela, decides usar tus conocimientos del Teorema de Pitágoras para determinar qué tan lejos está entre tu casa y la escuela. Sabes que caminas 3 cuadras al este, y luego giras y caminas 7 cuadras hacia el norte para llegar a la escuela. ¿Es posible utilizar el Teorema de Pitágoras para ayudarte a determinar la distancia “en línea recta” entre tu casa y la escuela?

Determinar la distancia usando el teorema de Pitágoras

Se puede utilizar el Teorema de Pitágoras es para encontrar la distancia entre dos puntos.

Considerar los puntos (-1, 6) y (5, -3). Si trazamos estos puntos en una rejilla y los conectamos, hacen una línea diagonal. Dibuja una línea vertical hacia abajo desde (-1, 6) y una línea horizontal a la izquierda de (5, -3) para formar un triángulo rectángulo.

Figura\(\PageIndex{1}\)

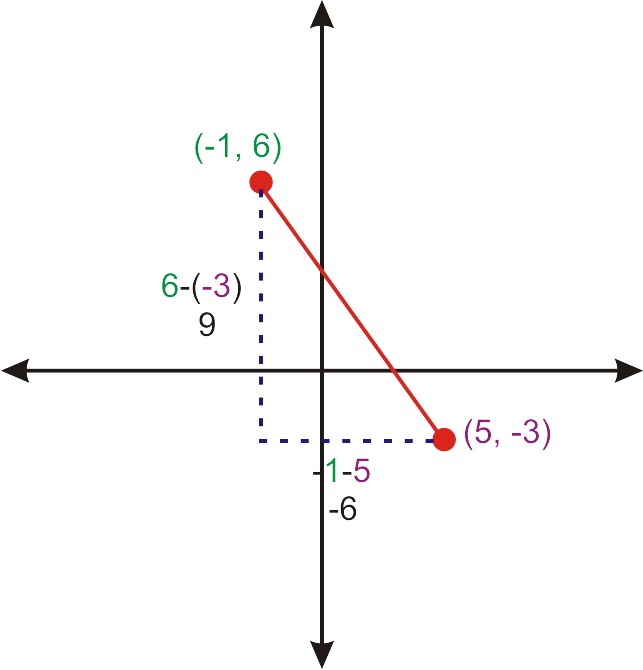
Ahora podemos encontrar la distancia entre estos dos puntos utilizando las distancias vertical y horizontal que determinamos a partir de la gráfica.

\(\begin{aligned} 9^2+(−6)^2 &=d^2 \\ 81+36 &=d^2 \\ 117 &=d^2\\ \sqrt{117}&=d \\ 3\sqrt{13}&=d\end{aligned}\)

Observe que los valores x se restaron entre sí para encontrar la distancia horizontal y los valores y se restaron entre sí para encontrar la distancia vertical. Si este proceso se generaliza para dos puntos (x_1, y_1) y (x_2, y_2), se deriva la Fórmula de Distancia.

\((x_1−x_2)^2+(y_1−y_2)^2=d^2\)

Figura\(\PageIndex{2}\)

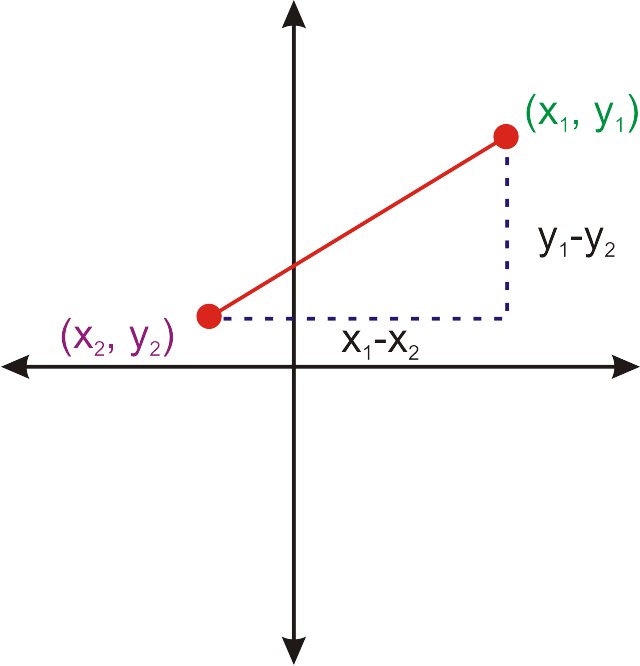
Este es el Teorema de Pitágoras con las diferencias verticales y horizontales entre (x_1, y_1) y (x_2, y_2). Tomando la raíz cuadrada de ambos lados resolverá el lado derecho para d, la distancia.

\(\sqrt{(x_1−x_2)^2+(y_1−y_2)^2}=d\)

Esta es la Fórmula de Distancia. Los siguientes problemas muestran cómo aplicar la fórmula de distancia.

Aplicación de la fórmula de distancia

1. Encuentra la distancia entre los dos puntos.

(4, 2) y (-9, 5)

Conecta cada par de puntos en la Fórmula de Distancia.

\(\begin{aligned} d&=\sqrt{(4−(−9))^2+(2−5)^2} \\ &=\sqrt{13^2+(−3)^2} \\ &=\sqrt{169+9} \\ &=\sqrt{178}\end{aligned}\)

2. Encuentra la distancia entre los dos puntos.

(-10, 3) y (0, -15)

Conecta cada par de puntos en la fórmula de distancia.

\(\begin{aligned} d&=\sqrt{(−10−0)^2+(3−(−15))^2}\\ &=\sqrt{(−10)^2+(18)^2}\\ &=\sqrt{100+324} \\ &=\sqrt{424} \\ &=2\sqrt{106}\end{aligned}\)

3. Encuentra la distancia entre los dos puntos.

(3, 1) y (2, -7)

Conecta cada par de puntos en la fórmula de distancia.

\(\begin{aligned} d&=\sqrt{(3−2)^2+(1−(−7))^2}\\ &=\sqrt{(1)^2+(8)^2}\\ &=\sqrt{1+64}\\ &=\sqrt{65}\end{aligned}\)

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le pidió que usara sus conocimientos del Teorema de Pitágoras para determinar qué tan lejos está entre su casa y la escuela.

Solución

Ya que sabes que el viaje a la escuela implica caminar 3 cuadras al este seguido de 7 cuadras al norte, puedes construir un triángulo en un sistema de coordenadas a partir de estas longitudes, así:

Figura\(\PageIndex{3}\)

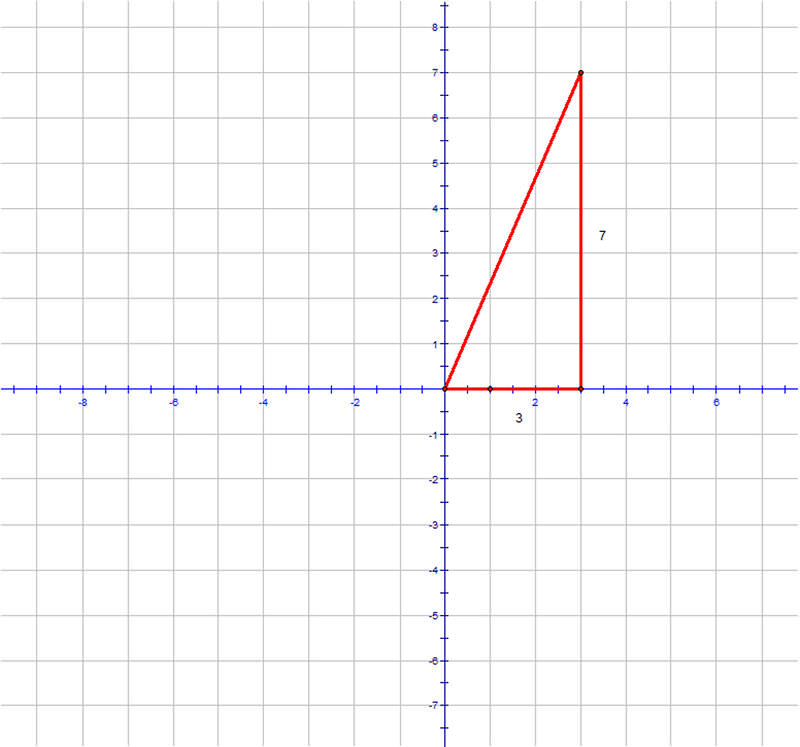
Desde que fuiste tres cuadras al este, la escuela tiene una coordenada “x” de 3. De igual manera, desde que fuiste 7 cuadras al norte, la escuela tiene una coordenada “y” de 7. Para encontrar la distancia en línea recta a la escuela, puedes usar la Fórmula de Distancia:

\(\begin{aligned} d&=(3−0)^2+(7−0)^2\\ &=\sqrt{(3)^2+(7)^2} \\ &=\sqrt{58}\end{aligned}\)

Esta es una distancia en línea recta de aproximadamente 7.6 cuadras.

Ejemplo\(\PageIndex{2}\)

Encuentra la distancia entre los dos puntos.

(3, 1) y (2, -7)

Solución

Conecta cada par de puntos en la fórmula de distancia.

\(\begin{aligned} d&=\sqrt{(3−2)^2+(1−(−7))^2}\\ &=\sqrt{(1)^2+(8)^2} \\ &=\sqrt{1+64}\\ &=\sqrt{65}\end{aligned}\)

Ejemplo\(\PageIndex{3}\)

Encuentra la distancia entre los dos puntos.

(5, -8) y (0, 3)

Solución

Conecta cada par de puntos en la fórmula de distancia.

\(\begin{aligned} d&=\sqrt{(5−0)^2+(−8−(3))^2} \\ &=(5)^2+(−11)^2 \\ &=\sqrt{25+121}\\ &=\sqrt{146}\end{aligned}\)

Ejemplo\(\PageIndex{4}\)

Encuentra la distancia entre los dos puntos.

(2, 6) y (2, 9)

Solución

Conecta cada par de puntos en la fórmula de distancia.

\(\begin{aligned} d&=\sqrt{(2−2)^2+(6−9)^2} \\ &=\sqrt{(0)^2+(−3)^2} \\ &=\sqrt{9}=3\end{aligned}\)

Revisar

Encuentra la distancia entre cada par de puntos. Redondea cada respuesta a la décima más cercana.

1. (2, 4) y (5, 10)
2. (1, 5) y (8, 9)
3. (-2, 3) y (6, 4)
4. (5, 7) y (5, 10)
5. (8, 12) y (15, 12)
6. (1, -4) y (25, -2)
7. (5, -6) y (3, 7)
8. (12, -9) y (-1, 5)
9. (-3, 14) y (8, 10)
10. (-11, 3) y (-5, 1)
11. (5, 2) y (11, 13)
12. (8, 10) y (9, -6)

Encuentra el perímetro de cada triángulo. Redondea cada respuesta a la décima más cercana.

13. \(A(3,−5),B(−5,−8),C(−2,7)\)
14. \(A(5,3),B(2,−7),C(−1,5)\)
15. \(A(1,2),B(1,5),C(4,5)\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.4.

vocabulario

Término	Definición
Fórmula de distancia	La distancia entre dos puntos\((x_1,y_1)\) y se\((x_2,y_2)\) puede definir como\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\).

Recursos adicionales

Elemento Interactivo

Video: La fórmula de la distancia

Práctica: Fórmula a distancia y el teorema de Pitágoras

Mundo real: Todo depende de la distancia