2.1.5: Seno y Coseno de Ángulos Complementarios

Última actualización
Guardar como PDF

Page ID: 107635

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Seno de un ángulo es igual al coseno de su complemento.

\(\Delta ABC\)es un triángulo rectángulo con\(m\angle C=90^{\circ}\) y\(\sin A=k\). ¿Qué es\(\cos B\)?

Seno y Coseno de Ángulos Complementarios

Recordemos que el seno y el coseno de los ángulos son relaciones de pares de lados en triángulos rectos.

El seno de un ángulo en un triángulo rectángulo es la relación del lado opuesto al ángulo a la hipotenusa.
El coseno de un ángulo en un triángulo rectángulo es la relación del lado adyacente al ángulo a la hipotenusa.

En los problemas a continuación, explorarás cómo se relacionan el seno y el coseno de los ángulos en un triángulo rectángulo.

Echemos un vistazo a algunos problemas de ejemplo.

1. Considera el triángulo rectángulo a continuación. Encuentra el seno y el coseno de los ángulos A y B en términos de a, b y c. ¿Qué notas?

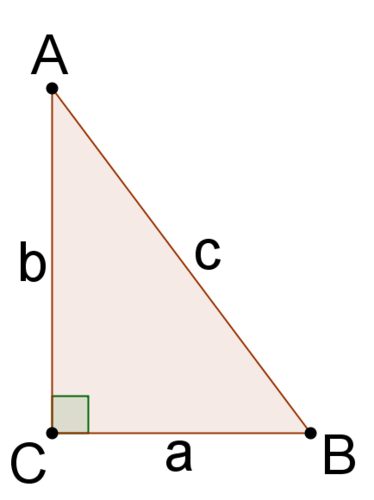
\(\sin A=\dfrac{a}{c}\),\(\sin B=\dfrac{b}{c}\),\(\cos A=\dfrac{b}{c}\),\(\cos B=\dfrac{a}{c}\) Tenga en cuenta que\(\sin A=\cos B\) y\(\sin B=\cos A\).

2. Considera el triángulo del problema anterior. ¿Cómo se\(\angle A\) relaciona con\(\angle B\)?

La suma de las medidas de los tres ángulos en un triángulo es\(180^{\circ}\). Esto significa que\(m\angle A+m\angle B+m\angle C=180^{\circ}\). \(\angle C\)es un ángulo recto así\(m\angle C=90^{\circ}\). Por lo tanto,\(m\angle A+m\angle B=90^{\circ}\). Los ángulos A y B son ángulos complementarios porque su suma es\(90^{\circ}\).

En #1 viste eso\(\sin A=\cos B\) y\(\sin B=\cos A\). Esto significa que el seno y el coseno de los ángulos complementarios son iguales.

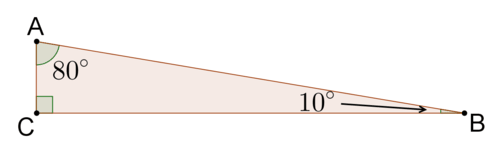
3. Encontrar\(80^{\circ}\) y\(\cos 10^{\circ}\). Explique el resultado.

\(\sin 80^{\circ}\approx 0.985\)y\(\cos 10^{\circ}\approx 0.985\). \(\sin 80^{\circ}=\cos 10^{\circ}\)porque\(80^{\circ}\) y\(10^{\circ}\) son medidas angulares complementarias. \(\sin 80^{\circ}\)y\(\cos 10^{\circ}\) son las proporciones de los mismos lados de un triángulo rectángulo, como se muestra a continuación.

Ejemplo\(\PageIndex{1}\)

Antes, se le preguntó qué es\(\cos B\).

\(\Delta ABC\)es un triángulo rectángulo con\(m\angle C=90^{\circ}\) y\(\sin A=k\). ¿Qué es\(\cos B\)?

Solución

\(\angle A\)y\(\angle B\) son complementarios porque son los dos ángulos no rectos de un triángulo rectángulo. Esto significa que\(\sin A=\cos B\) y\(\sin B=\cos A\). Si\(\sin A=k\), entonces\(\cos B=k\) también.

Ejemplo\(\PageIndex{2}\)

Si\(\sin 30^{\circ}=\dfrac{1}{2}\),\(\cos\stackrel?{=}\dfrac{1}{2}\).

Solución

El seno y el coseno de los ángulos complementarios son iguales. \(90^{\circ}−30^{\circ}=60^{\circ}\)es complementario a\(30^{\circ}\). Por lo tanto,\(\cos 60^{\circ}=\dfrac{1}{2}\).

Ejemplo\(\PageIndex{3}\)

Considera el triángulo rectángulo a continuación. Encontrar\(\tan A\) y\(\tan B\).

Solución

\(\tan A=\dfrac{a}{b}\)y\(\tan B=\dfrac{b}{a}\).

Ejemplo\(\PageIndex{4}\)

En general, ¿cuál es la relación entre las tangentes de los ángulos complementarios?

Solución

En general, las tangentes de los ángulos complementarios son recíprocas.

Revisar

1. ¿Cómo se relacionan los dos ángulos no rectos en un triángulo rectángulo? Explique.

2. ¿Cómo se relacionan el seno y el coseno de los ángulos complementarios? Explique.

3. ¿Cómo se relacionan las tangentes de los ángulos complementarios? Explique.

Que A y B sean los dos ángulos no rectos en un triángulo rectángulo.

4. Si\(\tan A=\dfrac{1}{2}\), ¿qué es\(\tan B\)?

5. Si\(\sin A=\dfrac{7}{10}\), ¿qué es\(\cos B\)?

6. \(\cos A=\dfrac{1}{4}\)¿Si qué es\(\sin B\)?

7. Si\(\sin A=\dfrac{3}{5}\),\(\cos \stackrel?{=} \dfrac{3}{5}\)?

8. Simplificar\(\dfrac{\sin A+\cos B}{2}\).

9. \(\tan A=\dfrac{2}{3}\)¿Si qué es\(\tan B\)?

10. Si\(\tan B=\dfrac{1}{5}\), ¿qué es\(\tan A\)? ¿Qué ángulo es más grande,\(\angle A\) o\(\angle B\)?

Resolver para\(\theta\).

11. \(\cos 30^{\circ}=\sin \theta\)

12. \(\sin 75^{\circ}=\cos \theta\)

13. \(\cos 52^{\circ}=\sin \theta\)

14. \(\sin 18^{\circ}=\cos \theta\)

15. \(\cos 49^{\circ}=\sin \theta\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.3.

vocabulario

Término	Definición
Ángulos complementarios	Los ángulos complementarios son un par de ángulos con una suma de\(90^{\circ}\).
coseno	El coseno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud de la hipotenusa.
seno	El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa.

Recursos adicionales

Elemento Interactivo

Práctica: Seno y Coseno de Ángulos Complementarios