2.3.5: Signos de Funciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 107672

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\(x\)y\(y\) valores de una función; signos de funciones basados en cuadrantes.

Dominio, Rango y Signos de Funciones Trigonométricas

Un día estás garabateando en la clase de arte cuando dibujas un círculo. Después dibujas algunas líneas que se extienden hacia afuera desde el centro hasta el borde del círculo. Dibujas un triángulo con el eje\(x\) "”, y te das cuenta de que estás pensando de nuevo en tu clase de matemáticas.

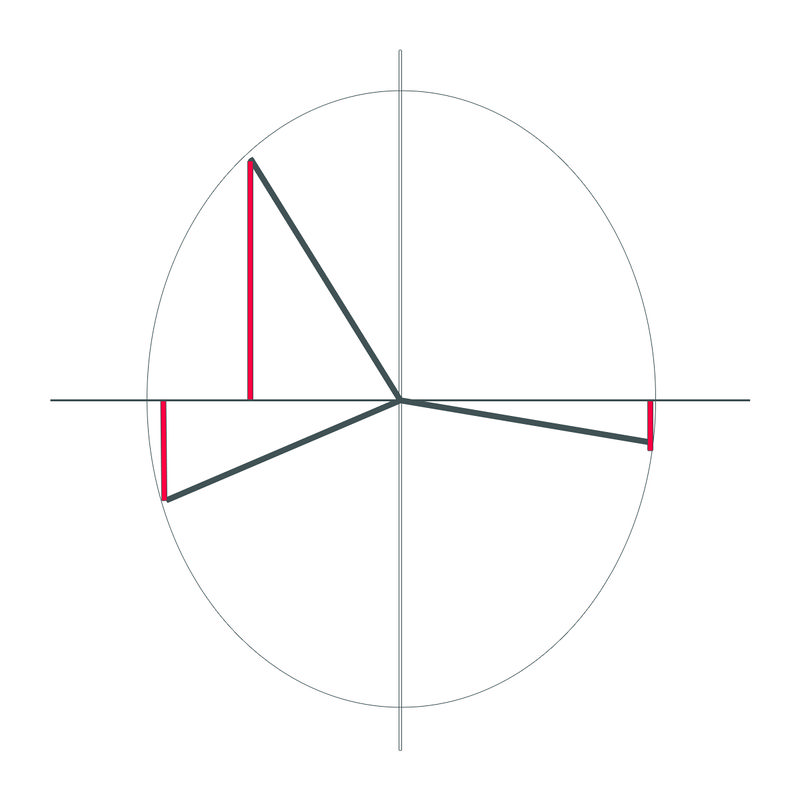
F-D_F682328267E292A04445F3B590C7AF82CA05003C9E07303B03968530+Image_Tiny+Image_Tiny.jpg — Figura\(\PageIndex{1}\)

Se nota que la relación para la función sinusoidal implica la longitud del lado opuesto al ángulo dividido por la longitud de la hipotenusa. Pero si bien la hipotenusa es siempre un número positivo, el signo del lado opuesto puede ser diferente, dependiendo de en qué cuadrante se dibuje el ángulo.

¿Se puede determinar cuál será el signo de la función sinusoidal en cada uno de los cuatro cuadrantes, con base en el conocimiento de la relación que define la función sinusoidal?

Dominio y Rango de Funciones Trigonométricas

Si bien las funciones trigonométricas pueden parecer bastante diferentes de otras funciones con las que ha trabajado, de hecho son como cualquier otra función. Podemos pensar en una función trigonométrica en términos de “entrada” y “salida”. La entrada es siempre un ángulo. La salida es una relación de lados de un triángulo. Si piensas en las funciones trigonométricas de esta manera, puedes definir el dominio y el rango de cada función.

Consideremos primero las funciones seno y coseno. La entrada de cada una de estas funciones es siempre un ángulo, y como aprendiste en las secciones anteriores, estos ángulos pueden tomar cualquier valor de número real. Por lo tanto la función seno y coseno tienen el mismo dominio, el conjunto de todos los números reales,\(R\). Podemos determinar el rango de las funciones si pensamos en el hecho de que el seno de un ángulo es la\(y\) coordenada −del punto donde el lado terminal del ángulo intersecta el círculo unitario. El coseno es la\(x\) coordenada −de ese punto. Ahora recordemos que en el círculo unitario, definimos las funciones trigonométricas en términos de un triángulo con hipotenusa 1.

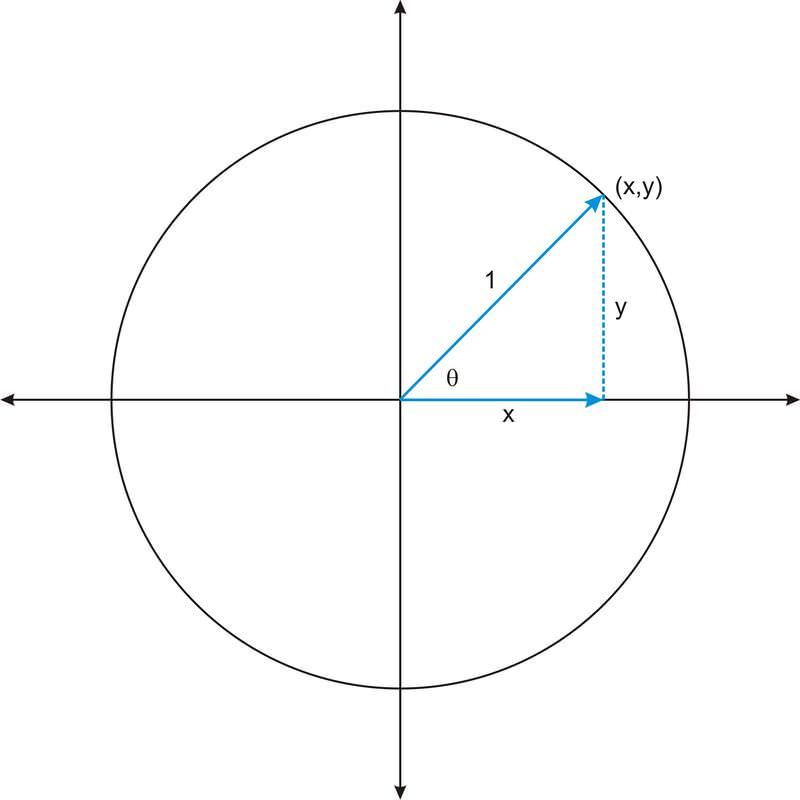
F-D_199b94ac4ea7b9e5f96e29883e4890516f5412fdd684479d769e061a+image_tiny+image_tiny.jpg — Figura\(\PageIndex{2}\)

En este triángulo rectángulo,\(x\) y\(y\) están las longitudes de las patas del triángulo, que deben tener longitudes menores a 1, la longitud de la hipotenusa. Por lo tanto, los rangos de la función seno y coseno no incluyen valores mayores a uno. Sin embargo, los rangos contienen valores negativos. Cualquier ángulo cuyo lado terminal esté en el tercer o cuarto cuadrante tendrá una\(y\) coordenada −negativa, y cualquier ángulo cuyo lado terminal esté en el segundo o tercer cuadrante tendrá una\(x\) coordenada −negativa.

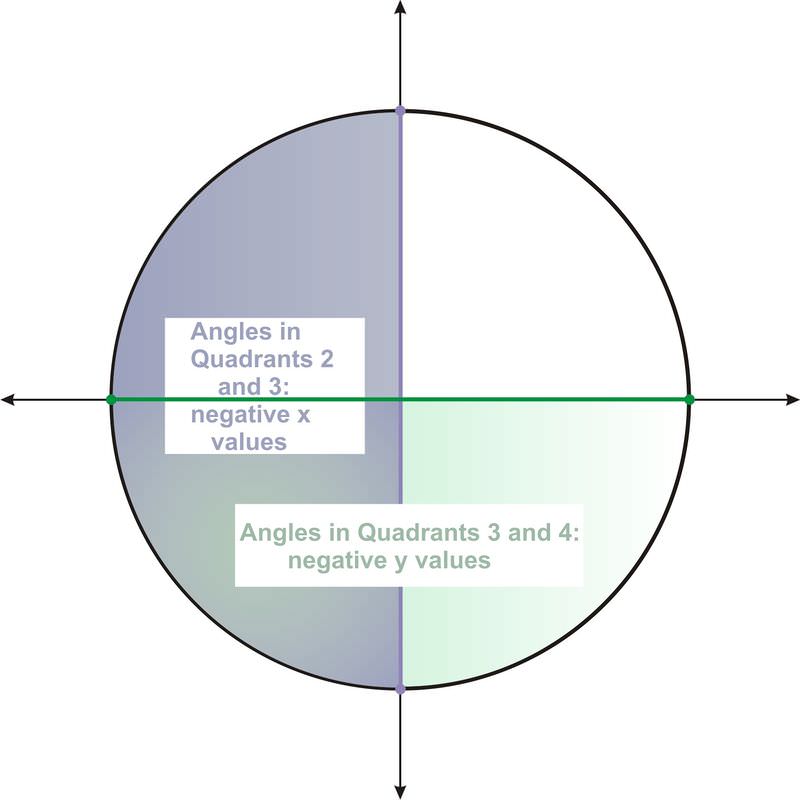
F-d_1a0e046e34beaca76943b8ad3d7849f5f7b871f65772cddc871f771b+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

En cualquier caso, el valor mínimo es -1. Por ejemplo,\(\cos 180^{\circ} =−1\) y\(\sin 270^{\circ} =−1\). Por lo tanto, la función senoidal y coseno ambas tienen un rango de -1 a 1.

La siguiente tabla resume los dominios y rangos de estas funciones:

	Dominio	Rango
Sine	\(\theta =R\)	\(−1\leq y\leq 1\)
Coseno	\(\theta =R\)	\(−1\leq y\leq 1\)

Conocer el dominio y rango de la función coseno y seno puede ayudarnos a determinar el dominio y rango de la función secante y cosecante. Consideremos primero las funciones sinusoidales y cosecantes, que como mostramos anteriormente, son recíprocas. La función cosecante se definirá siempre y cuando el valor sinusoidal no sea 0. Por lo tanto, el dominio de la función cosecante excluye todos los ángulos con valor sinusoidal 0, que son\(0^{\circ}\)\(180^{\circ}\),\(360^{\circ}\),, etc.

En el Capítulo 2 analizarás las gráficas de estas funciones, lo que te ayudará a ver por qué la relación recíproca da como resultado un rango particular para la función cosecante. Aquí indicaremos este rango, y en las preguntas de revisión explorarás valores de la función sinusoidal y cosecante para comenzar a verificar este rango, así como el dominio y rango de la función secante.

Función	Dominio	Rango
Tangente	\(\theta \in R,\theta \neq 90,270,450 \ldots\)	Todos los reales
Cotangente	\(\theta \in R,\theta \neq 0,180,360 \ldots\)	Todos los reales

Ahora consideremos las funciones tangente y cotangente. La función tangente se define como\(\tan \theta =\dfrac{y}{x}\). Por lo tanto, el dominio de esta función excluye los ángulos para los que el par ordenado tiene una\(x\) coordenada −coordenada de 0:\(90^{\circ}\)\(270^{\circ}\),, etc. La función cotangente se define como\(\cot \theta =\dfrac{x}{y}\), por lo que el dominio de esta función excluirá los ángulos para los que el par ordenado tenga una\(y\) coordenada −coordenada de 0: \(0^{\circ} \),\(180^{\circ}\)\(360^{\circ}\),, etc.

Función	Dominio	Rango
Tangente	\(\theta \in R, \theta \neq 90,270,450\ldots\)	Todos los reales
Cotangente	\(\theta \in R,\theta \neq 0 ,180 ,360 \ldots\)	Todos los reales

Conocer los rangos de estas funciones te indica los valores que debes esperar cuando determinas el valor de una función trigonométrica de un ángulo. No obstante, para muchos problemas necesitarás identificar el signo de la función de un ángulo: ¿Es positivo o negativo?

Al determinar los rangos de las funciones seno y coseno anteriores, comenzamos a categorizar los signos de estas funciones en términos de los cuadrantes en los que se encuentran los ángulos. La siguiente figura resume los signos de los ángulos en los 4 cuadrantes.

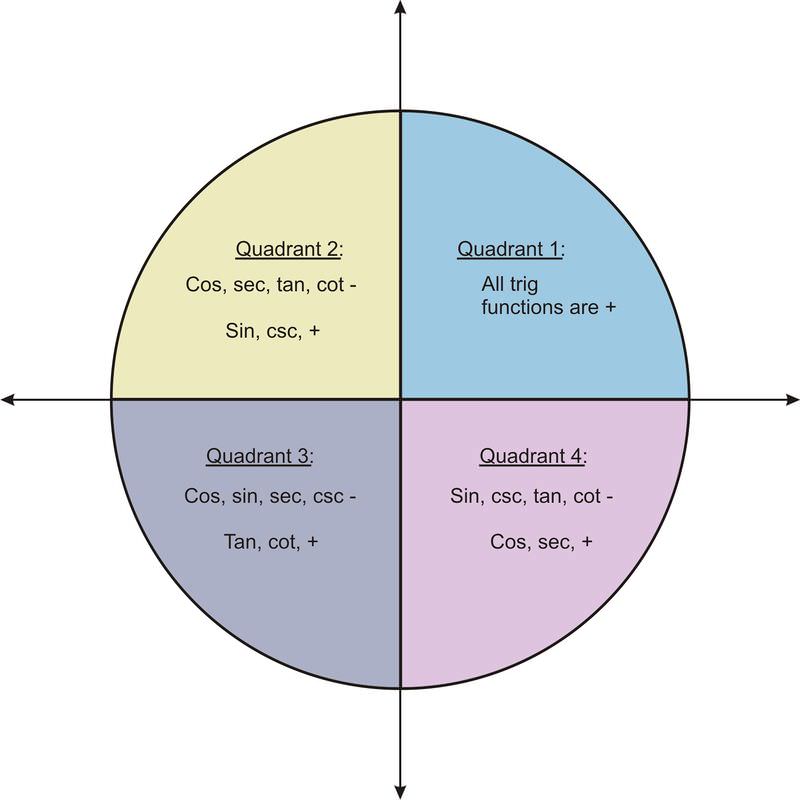
F-d_907767c6ef64cd76bbdc0e2cbc904945e3c3faa187e8b517481396c7+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

Una manera fácil de recordar esto es “A ll S tudents T ake C alculus”. Cuadrante I: Los valores de A ll son positivos, Cuadrante II: S ine es positivo, Cuadrante III: T angente es positivo y Cuadrante IV: C osina es positiva. Este sencillo dispositivo de memoria te ayudará a recordar qué funciones trigonométricas son positivas y dónde.

Declarar el Signo

1. Declarar el signo de\(\cos 100^{\circ}\)

El ángulo\(100^{\circ}\) está en el segundo cuadrante. Por lo tanto, la\(x\) coordenada −es negativa y así\(\cos 100^{\circ}\) es negativa.

2. Declarar el signo de\(\csc 220^{\circ}\)

El ángulo\(220^{\circ}\) está en el tercer cuadrante. Por lo tanto, la\(y\) coordenada −es negativa. Entonces el seno, y el cosecante son negativos.

3. Declarar el signo de\(\tan 370^{\circ}\)

El ángulo\(370^{\circ}\) está en el primer cuadrante. Por lo tanto, el valor tangente es positivo.

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le pidió que determinara cuál será el signo de la función sinusoidal en cada uno de los cuatro cuadrantes.

Solución

Dado que la función seno se define como la longitud del lado opuesto dividido por la longitud de la hipotenusa, el signo de la función sinusoidal es el signo de la coordenada y para cualquier cuadrante que se esté considerando. En los cuadrantes 1 y 2, la coordenada “y” es positiva, por lo que la función sinusoidal es positiva. En los cuadrantes 3 y 4, la coordenada y es negativa, por lo que la función sinusoidal también es negativa.

Ejemplo\(\PageIndex{2}\)

Declarar el signo de\(\cos 70^{\circ}\)

Solución

El ángulo\(70^{\circ}\) está en el primer cuadrante. El coseno se define como el lado adyacente dividido por la hipotenusa. Dado que la hipotenusa del círculo unitario es uno y el lado adyacente es la\(x\) coordenada, el signo de la función coseno está determinado por el signo de la\(x\) coordenada. Ya que\(70^{\circ}\) está en el primer cuadrante, el\(x\) valor es positivo. Por lo tanto, el valor del coseno es positivo.

Ejemplo\(\PageIndex{3}\)

Declarar el signo de\(\sin 130^{\circ}\)

Solución

El ángulo\(130^{\circ}\) está en el segundo cuadrante. El seno se define como el lado opuesto dividido por la hipotenusa. Dado que la hipotenusa del círculo unitario es uno y el lado opuesto es la coordenada y, el signo de la función sinusoidal está determinado por el signo de la\(y\) coordenada -. Ya que\(130^{\circ}\) está en el segundo cuadrante, el\(y\) valor es positivo. Por lo tanto, el valor sinusoidal es positivo.

Ejemplo\(\PageIndex{4}\)

Declarar el signo de\(\tan 250^{\circ}\)

Solución

El ángulo\(250^{\circ}\) está en el tercer cuadrante. La tangente se define como el lado opuesto dividido por el lado adyacente. En el tercer cuadrante, los\(x\) valores son negativos, y los valores y son negativos. Un negativo dividido por un negativo equivale a un positivo. Por lo tanto la tangente de\(250^{\circ}\) es positiva.

Revisar

¿En qué cuadrantes es positiva la función sinusoidal?
¿En qué cuadrantes es negativa la función cotangente?
¿En qué cuadrantes es negativa la función coseno?
¿En qué cuadrantes es positiva la función tangente?
¿Para qué ángulos está indefinida la función cosecante?
Declarar el signo de\(\sin 510^{\circ} \).
Declarar el signo de\(\cos 315^{\circ} \).
Declarar el signo de\(\tan 135^{\circ} \).
Indicar el signo de\(\cot 220^{\circ} \).
Indicar el signo de\(\csc 40^{\circ} \).
Indicar el signo de\(\cos 330^{\circ} \).
Indicar el signo de\(\sin 60^{\circ} \).
Indicar el signo de\(\sec −45^{\circ} \).
Explique por qué la función cosecante nunca es igual a 0.
Utilizando sus conocimientos de dominio y alcance, haga un posible boceto para\(y= \sin x\).

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.22.

El vocabulario

Término	Definición
dominio	El dominio de una función es el conjunto de\(x\) -valores para el que se define la función.
Rango	El rango de una función es el conjunto de\(y\) -valores para el que se define la función.

Recursos adicionales

Elemento Interactivo

Video: Dominio, Rango y Signos de Funciones Trigonométricas

Práctica: Signos de funciones trigonométricas