2.3.7: Ángulos de referencia y ángulos en el círculo unitario

Última actualización
Guardar como PDF

Page ID: 107649

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Formado entre el lado terminal de un ángulo y la parte más cercana del\(x\) eje.

Cuando entras a clase de matemáticas algún día, tu profesor tiene una sorpresa para la clase. Vas a jugar series de juegos relacionados con las cosas que has estado aprendiendo en clase. Para el primer juego, tu profesor entrega a cada grupo de alumnos un spinner con un eje\(x\) "" y\(y\) "” marcado. El juego es ver cuántos ángulos identificas correctamente. No obstante, en este juego, se supone que debes dar lo que se llama el "ángulo de referencia”. Giras tu spinner tres veces. Cada imagen de abajo muestra uno de los giros:

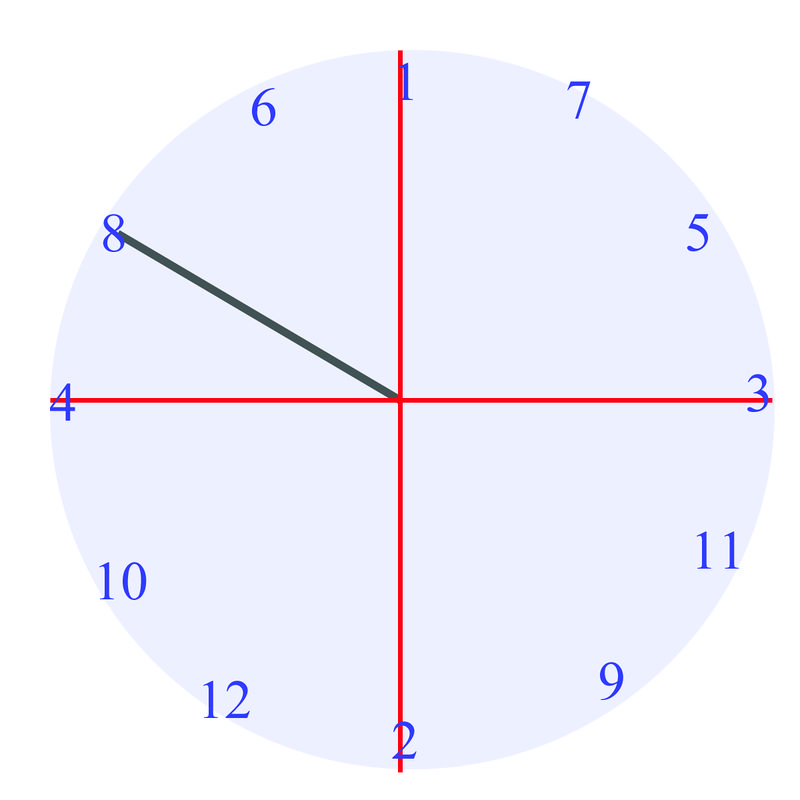
f-d_b05955a097cf2386d0101bd4052a28b5cb85a1769a463e42338b4ea9+image_tiny+image_tiny.jpg — Figura\(\PageIndex{1}\)

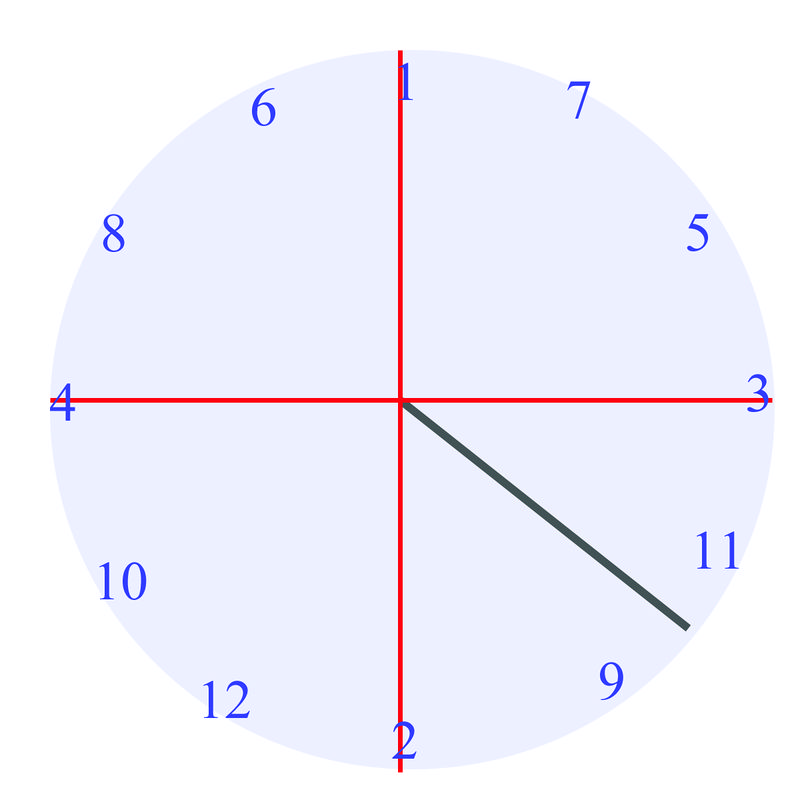
F-D_164221A56b4adea0f5657b59f18ec405669aa046fbbd6422ef447855+image_tiny+image_tiny.jpg — Figura\(\PageIndex{2}\)

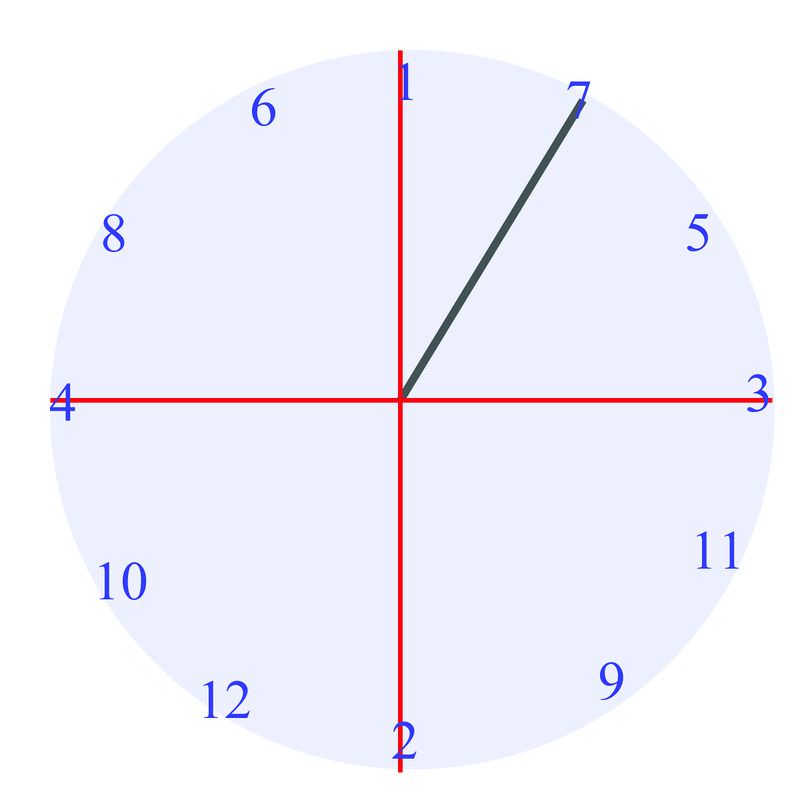
F-d_b1c6e1eb4ba05422215d66621cba579104170c536c2533497854e407+image_tiny+image_tiny.jpg — Figura\(\PageIndex{3}\)

¿Se pueden identificar correctamente los ángulos de referencia para estas imágenes?

Ángulos de Referencia

Considera el ángulo\(150^{\circ}\). Si graficamos este ángulo en posición estándar, vemos que el lado terminal de este ángulo es un reflejo del lado terminal de\(30^{\circ}\), a través del\(y\) eje −axis.

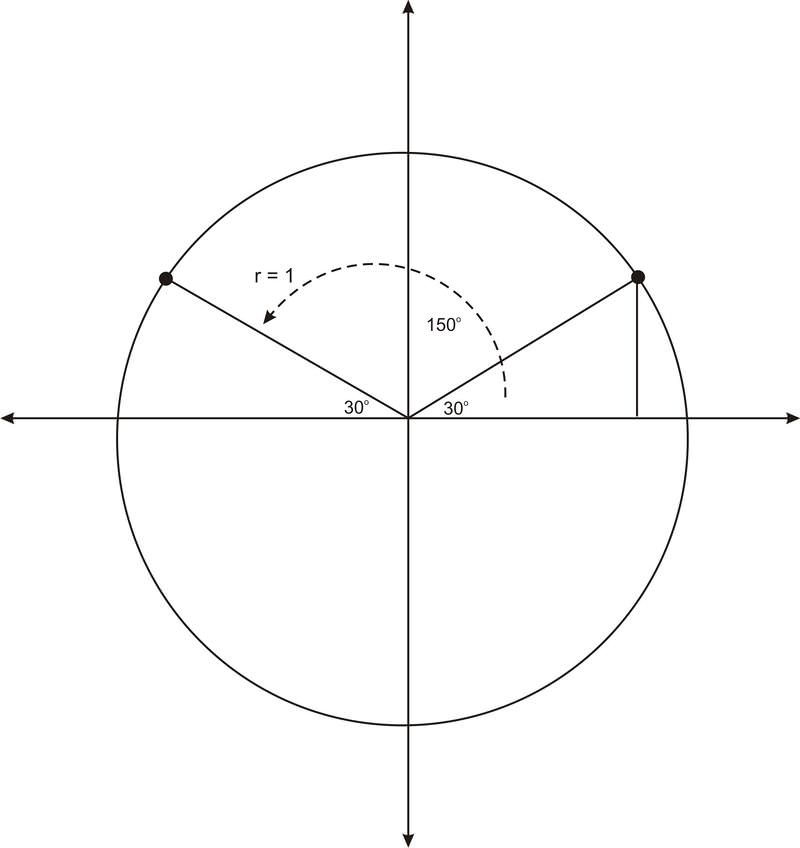
f-d_b1c40e370d12f7ff4385b9ec8af6aec8a3c0bd4db24bbffa0baaee23+image_tiny+image_tiny.jpg — Figura\(\PageIndex{4}\)

Observe que\(150^{\circ}\) hace un\(30^{\circ} \) ángulo con el\(x\) eje negativo. Por lo tanto decimos que\(30^{\circ}\) es el ángulo de referencia para\(150^{\circ}\). Formalmente, el ángulo de referencia de un ángulo en posición estándar es el ángulo formado con la porción más cercana\(x\) del eje. Observe que\(30^{\circ}\) es el ángulo de referencia para muchos ángulos. Por ejemplo, es el ángulo de referencia para\(210^{\circ}\) y para\(−30^{\circ}\).

En general, identificar el ángulo de referencia para un ángulo te ayudará a determinar los valores de las funciones trigonométricas del ángulo.

Identificación de ángulos de referencia

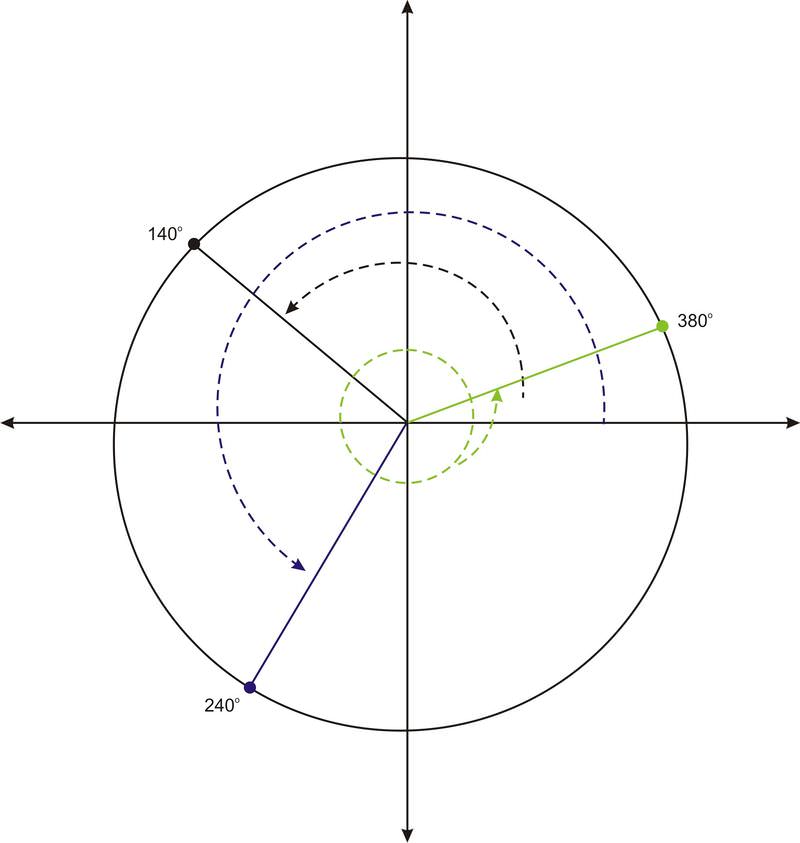
Grafica cada uno de los siguientes ángulos e identifica sus ángulos de referencia.

a.\(140^{\circ}\)

\(140^{\circ} \)hace\(40^{\circ} \) ángulos con el\(x\) eje negativo. Por lo tanto el ángulo de referencia es\(40^{\circ} \).

b.\(240^{\circ}\)

\(240^{\circ}\)hace un\(60^{\circ}\) ángulo con el\(x\) eje negativo. Por lo tanto, el ángulo de referencia es\(60^{\circ}\)

c.\(380^{\circ}\)

\(380^{\circ} \)es una rotación completa de\(360^{\circ}\), más un adicional\(20^{\circ}\). Entonces este ángulo es co-terminal con\(20^{\circ}\), y\(20^{\circ}\) es su ángulo de referencia.

F-d_9b5b8fa783cdd2c552a57581a0fd038c86dee30abb207baf7a031849+image_tiny+image_tiny.jpg — Figura\(\PageIndex{5}\)

Determinar el valor de las funciones trigonométricas

1. Encuentra el par ordenado para\(240^{\circ}\) y úsalo para encontrar el valor de\(\sin 240^{\circ}\).

\(\sin 240^{\circ} =−\dfrac{\sqrt{3}}{2}\)

Como encontramos en la parte b bajo la pregunta anterior, el ángulo de referencia para\(240^{\circ}\) es\(60^{\circ}\). La siguiente figura muestra\(60^{\circ}\) y los otros tres ángulos en el círculo unitario que tienen\(60^{\circ}\) como ángulo de referencia.

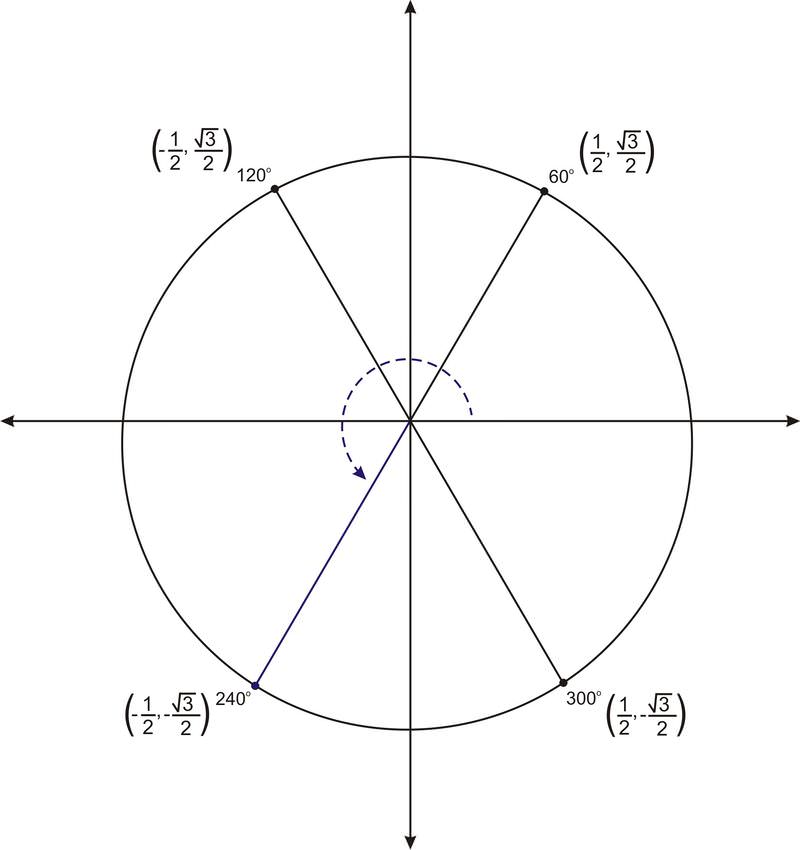
f-d_fd3b0aeaa10cadbdc44295f25c522982bdfdb129ea731a93234b8c1b+image_tiny+image_tiny.jpg — Figura\(\PageIndex{6}\)

El lado terminal del ángulo\(240^{\circ}\) representa una reflexión del lado terminal de\(60^{\circ}\) sobre ambos ejes. Entonces las coordenadas del punto son\(\left(−\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\). La coordenada y es el valor sinusoidal, entonces\(\sin 240^{\circ} =−\dfrac{\sqrt{3}}{2}\).

Así como muestra la figura anterior\(60^{\circ}\) y tres ángulos relacionados, podemos hacer gráficas similares para\(30^{\circ}\) y\(45^{\circ}\).

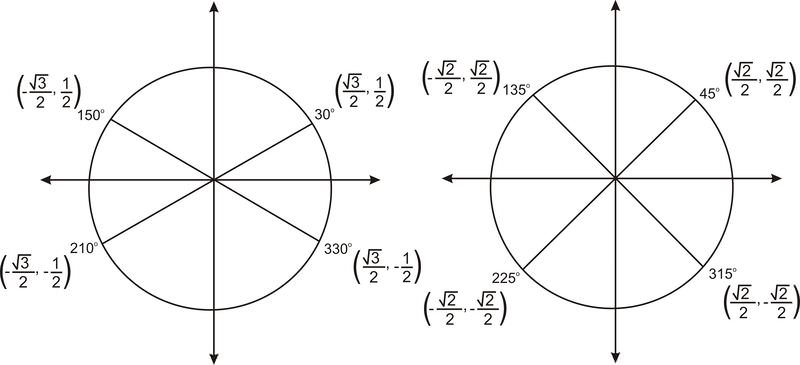
F-d_72e8e0753d930037ed1a6ba596ea441a1d31644b83b2c69a84e34e3e+image_tiny+image_tiny.jpg — Figura\(\PageIndex{7}\)

Conocer estos pares ordenados te ayudará a encontrar el valor de cualquiera de las funciones trigonométricas para estos ángulos.

2. Encuentra el valor de\(\cot 300^{\circ}\)

\(\cot 300^{\circ} =−\dfrac{1}{\sqrt{3}}\)

Usando la gráfica anterior, encontrarás que el par ordenado es\(\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\). Por lo tanto, el valor cotangente es\(\cot 300^{\circ}=\dfrac{x}{y}=\dfrac{\dfrac{1}{2}}{-\dfrac{\sqrt{3}}{2}}=\dfrac{1}{2} \times-\dfrac{2}{\sqrt{3}}=-\dfrac{1}{\sqrt{3}}\)

También podemos usar el concepto de ángulo de referencia y los pares ordenados que hemos identificado para determinar los valores de las funciones trigonométricas para otros ángulos.

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le preguntó si puede identificar correctamente los ángulos de referencia en las imágenes.

Solución

Ya que ya sabes medir ángulos de referencia, al examinar los hilanderos, sabes que el primer ángulo es\(30^{\circ}\), el segundo ángulo es\(45^{\circ}\), y el tercer ángulo lo es\(60^{\circ}\).

Ejemplo\(\PageIndex{2}\)

Grafica\(210^{\circ}\) e identifica su ángulo de referencia.

Solución

La gráfica de\(210^{\circ}\) se ve así:

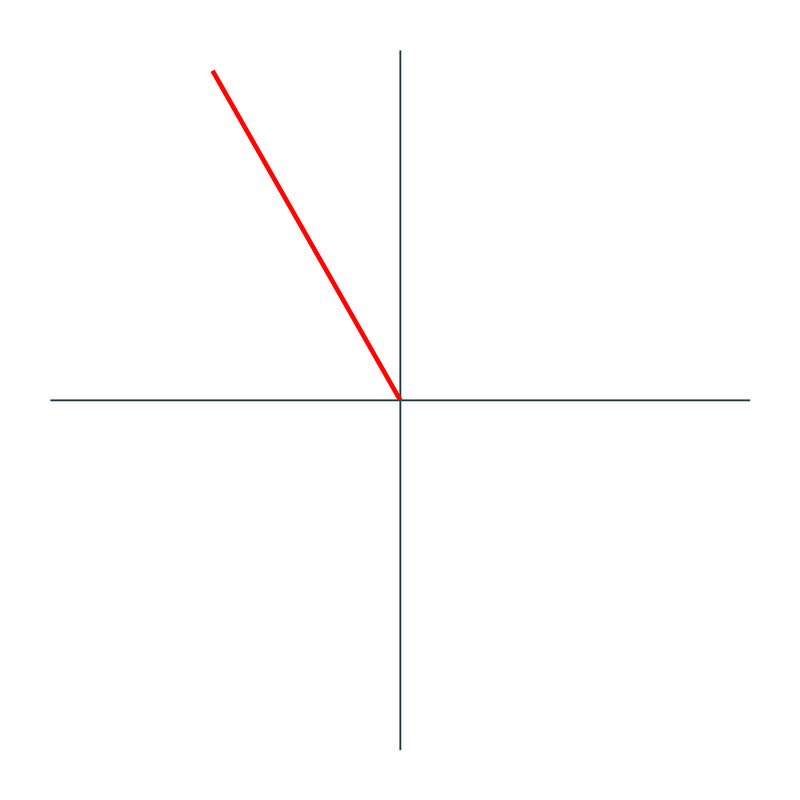
F-d_440f2b3492e6b4d4f903a334f27e5850cee79cc7fb3cbcc95cf2222a+image_tiny+image_tiny.jpg — Figura\(\PageIndex{8}\)

y como el ángulo hace un\(30^{\circ}\) ángulo con el eje "\(x\)" negativo, el ángulo de referencia es\(30^{\circ}\).

Ejemplo\(\PageIndex{3}\)

Grafica\(315^{\circ}\) e identifica su ángulo de referencia.

Solución

La gráfica de\(315^{\circ}\) se ve así:

F-d_f3fd552f39861092b450ab42ba68a69c58ec7c45cf25bfb2e13ca303+image_tiny+image_tiny.jpg — Figura\(\PageIndex{9}\)

y como el ángulo hace un\(45^{\circ}\) ángulo con el eje "\(x\)" positivo, el ángulo de referencia es\(45^{\circ}\).

Ejemplo\(\PageIndex{4}\)

Encuentra el par ordenado para\(150^{\circ}\) y úsalo para encontrar el valor de cos\(150^{\circ}\).

Solución

Ya que el ángulo de referencia es\(30^{\circ}\), sabemos que las coordenadas para el punto en el círculo unitario son\(\left(−\dfrac{\sqrt{3}}{2}, \dfrac{1}{2}\right)\). Esto es lo mismo que el valor para\(30^{\circ}\), excepto que la coordenada\(x\) "" es negativa en lugar de positiva. Sabiendo esto,

\(\cos 150^{\circ}=\dfrac{\text { adjacent }}{\text { hypotenuse }}=\dfrac{-\dfrac{\sqrt{3}}{2}}{1}=-\dfrac{\sqrt{3}}{2}\)

Revisar

Grafica\(100^{\circ}\) e identifica su ángulo de referencia.
Grafica\(200^{\circ}\) e identifica su ángulo de referencia.
Grafica\(290^{\circ}\) e identifica su ángulo de referencia.

Calcula cada valor usando el círculo unitario y los triángulos rectos especiales.

\(\sin 120^{\circ}\)
\(\cos 120^{\circ}\)
\(\csc 120^{\circ}\)
\(\cos 135^{\circ}\)
\(\sin 135^{\circ}\)
\(\tan 135^{\circ}\)
\(\sin 210^{\circ}\)
\(\cos 210^{\circ}\)
\(\cot 210^{\circ}\)\)
\(\sin 225^{\circ}\)
\(\cos 225^{\circ}\)
\(\sec 225^{\circ}\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.18.

El vocabulario

Término	Definición
Ángulo de referencia	Un ángulo de referencia es el ángulo formado entre el lado terminal del ángulo y el más cercano del\(x\) eje positivo o negativo.

Recursos adicionales

Elemento Interactivo

Video: Ángulos de referencia - Descripción general

Práctica: Ángulos de referencia y ángulos en el círculo unitario