2.4.2: Inversa por Mapeo
- Page ID
- 107689
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Refleja puntos del\(f(x)\) otro lado de la línea\(y = x\).
Tu instructor te da una función,\(f(x)=(x−1)^2+3\), dónde\(x\geq 1\), y te pide que encuentres la inversa. Todo está listo para comenzar a manipular la ecuación, cuando su Instructor especifique que debe encontrar la inversa graficando en lugar de por manipulación algebraica.
¿Eres capaz de hacer esto?
Encontrar la inversa mediante mapeo
Determinar una función inversa algebraicamente puede ser tanto complicado como difícil, por lo que es útil saber mapear\(f\) a\(f^{−1}\).
La gráfica de f se puede utilizar para producir la gráfica de\(f^{−1}\) aplicando el principio de reflexión inversa:
Los puntos\((a,b)\) y\((b,a)\) en el plano de coordenadas son simétricos con respecto a la línea\(y=x\).
Los puntos\((a,b)\) y\((b,a)\) son reflejos unos de otros a través de la línea\(y=x\).
Encontrar la inversa de una función
1. Encuentra la inversa de\(f(x)=\dfrac{1}{x−5}\) mapeando.
Desde la última sección, sabemos que lo inverso de esta función es\(y=\dfrac{5x+1}{x}\). Para encontrar la inversa mediante mapeo, elija varios puntos\(f(x)\), refleje los mismos usando el principio de reflexión y trazar. Nota: Las coordenadas de algunos de los puntos son redondeadas.
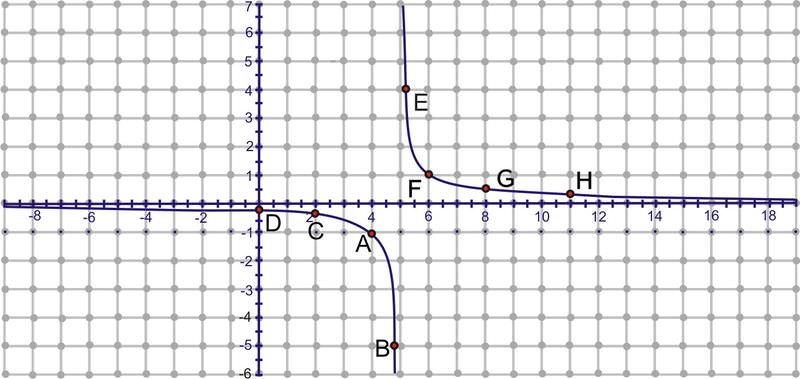
\(A: (4, -1)\)
\(B: (4.8, -5)\)
\(C: (2, -0.3)\)
\(D: (0, -0.2)\)
\(E: (5.3, 3.3)\)
\(F: (6, 1)\)
\(G: (8, 0.3)\)
\(H: (11, 0.2)\)
Ahora, toma estos ocho puntos, cambia el\(x\) y\(y\) y trama\((y,x)\). Conéctelos para hacer la función inversa.
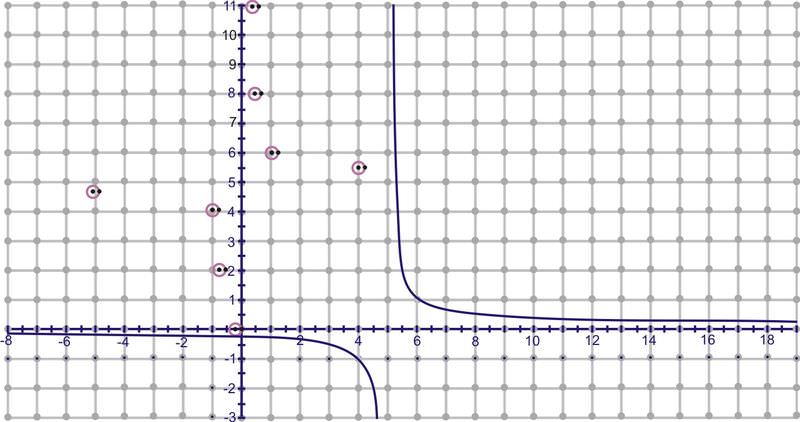
\(A^{−1}: (−1,4)\)
\(B^{−1}: (−5,4.8)\)
\(C^{−1}: (−0.3,2)\)
\(D^{−1}: (−0.2,0)\)
\(E^{−1}: (3.3,5.3)\)
\(F^{−1}: (1,6)\)
\(G^{−1}: (0.3,8)\)
\(H^{−1}: (0.2,11)\)
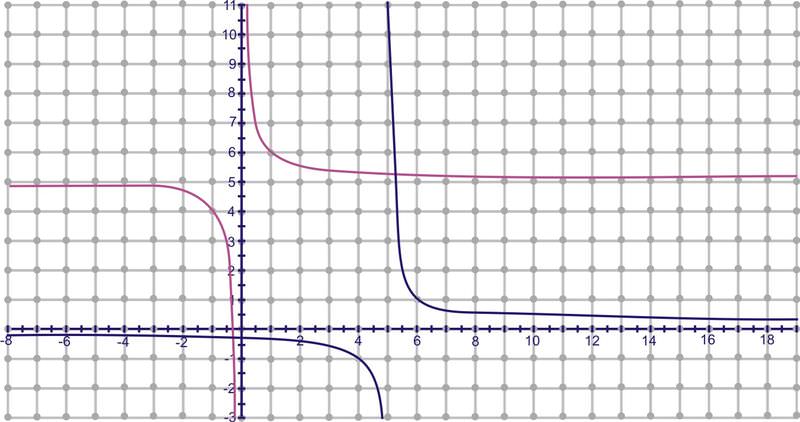
No todas las funciones tienen inversos que son uno a uno. Sin embargo, la inversa se puede modificar a una función uno a uno si se aplica un “dominio restringido” a la función inversa.
2. Encuentra la inversa de\(f(x)=x^2−4\).
Usemos el enfoque gráfico para éste. La función está graficada en azul y su inversa es roja.
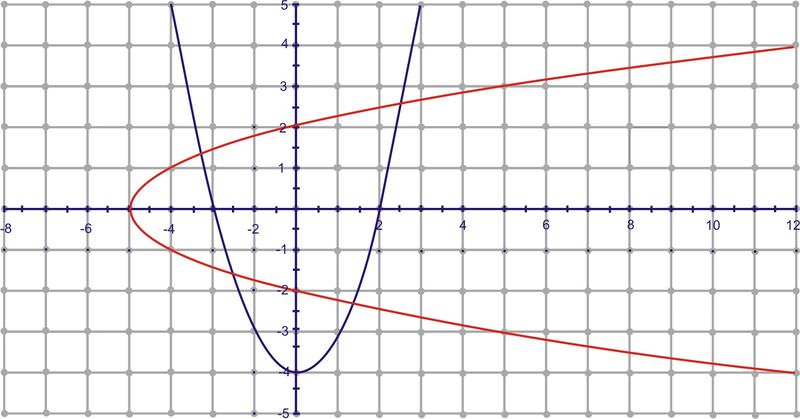
Claramente, la relación inversa no es una función porque no pasa la prueba de línea vertical. Esto se debe a que todas las parabolas fallan en la prueba de línea horizontal. Para “hacer” la inversa una función, restringimos el dominio de la función original. Para las parábola, esto es bastante sencillo. Para encontrar la inversa de esta función algebraicamente, obtenemos\(f^{−1}(x)=\sqrt{x+4}\). Técnicamente, sin embargo, lo inverso se\(\pm\sqrt{x+4}\) debe a que la raíz cuadrada de cualquier número podría ser positiva o negativa. Entonces, la inversa de\(f(x)=x^2−4\) es ambas partes de la ecuación de raíz cuadrada,\(\sqrt{x+4}\) y\(−\sqrt{x+4}\). \(\sqrt{x+4}\)cederá la porción superior de la parábola horizontal y\(−\sqrt{x+4}\) cederá la mitad inferior. Tenga cuidado, porque si solo grafica\(f^{−1}(x)=\sqrt{x+4}\) en su calculadora gráfica, solo graficará la parte superior de la inversa.
Esta técnica de seccionar la inversa se aplica para encontrar la inversa de funciones trigonométricas porque es periódica.
3. Encuentra la inversa del\(f(x)=\dfrac{x−1}{3x+2}\) mapeo.
Para encontrar la inversa mediante mapeo, elija varios puntos\(f(x)\), refleje los mismos usando el principio de reflexión y trazar. Nota: Las coordenadas de algunos de los puntos son redondeadas.
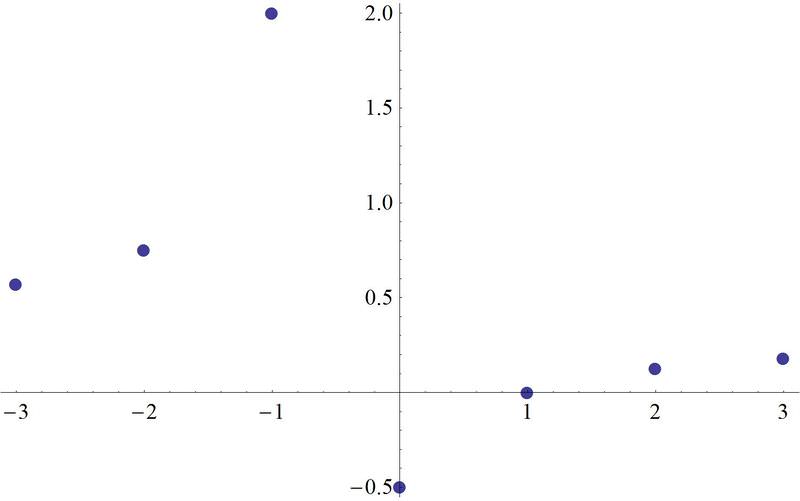
\(A: (0, -.5)\)
\(B: (-1, 2)\)
\(C: (1, 0)\)
\(D: (-2, .75)\)
\(E: (2, .125)\)
\(F: (-3, .57)\)
\(G: (3, .18)\)
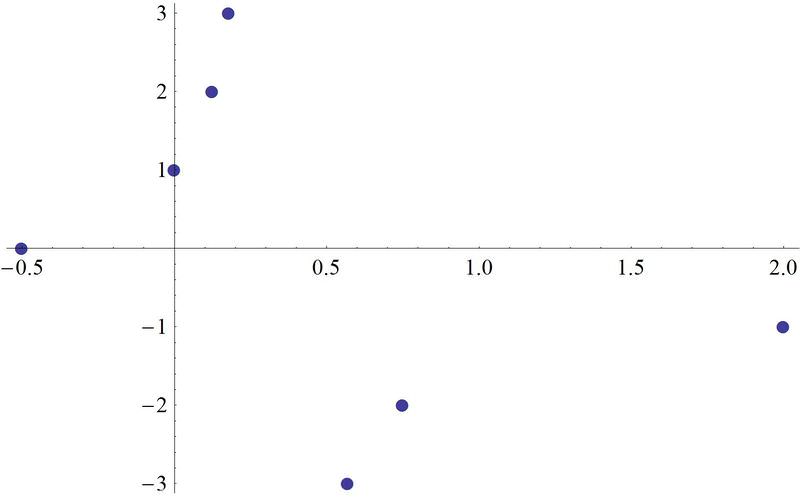
Ahora, toma estos siete puntos, cambia el\(x\) y\(y\) y trama\((y,x)\). Conéctelos para hacer la función inversa.
\(A^{−1}: (−.5,0)\)\)
\(B^{−1}: (2,−1)\)
\(C^{−1}: (0,1)\)
\(D^{−1}: (.75,−2)\)
\(E^{−1}: (.125,2)\)
\(F^{−1}: (.57,−3)\)
\(G^{−1}: (.18,3)\)
No todas las funciones tienen inversos que son uno a uno. Sin embargo, la inversa se puede modificar a una función uno a uno si se aplica un “dominio restringido” a la función inversa.
Anteriormente, se le pidió que encontrara la inversa de una función.
La ecuación original es\(f(x)=(x−1)^2+3\).
Solución
Aquí hay una gráfica de la función:
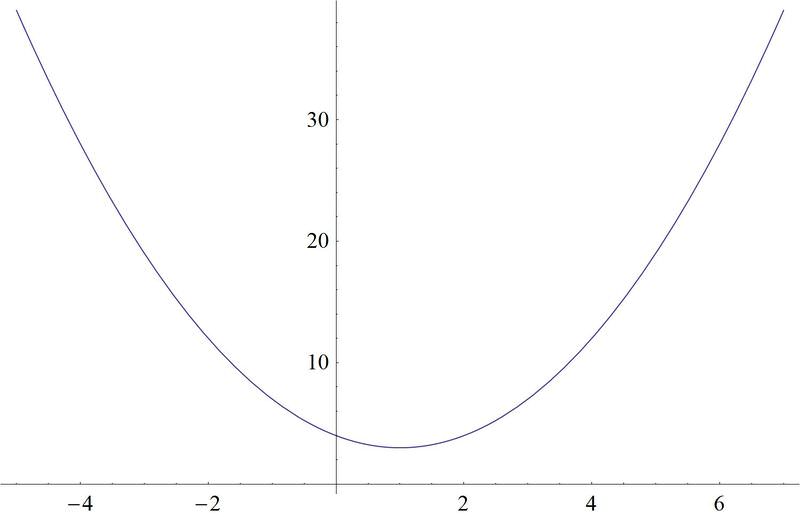
Observe que el dominio de la función bajo examen tiene que restringirse a 1 o mayor, para que la función pase la prueba de línea horizontal. Algunos puntos que se encuentran en esta gráfica son:
\(A: (1, 3)\)
\(B: (2, 4)\)
\(C: (3, 7)\)
Para mapear la función inversa, primero tome cada punto y cambie los valores "\(x\)" y ""\(y\) "”:
\(A^{−1}: (3,1)\)
\(B^{−1}: (4,2)\)
\(C^{−1}: (7,3)\)
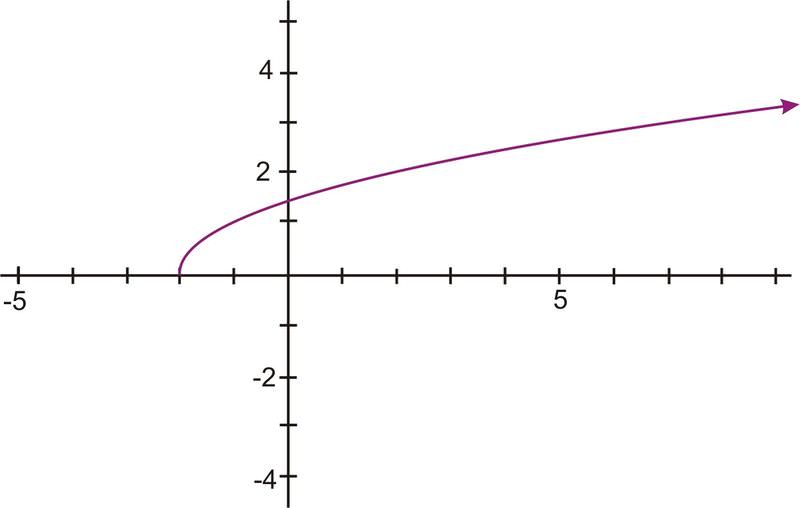
Entonces conecta estos puntos, y podrás ver la gráfica de la función inversa. El gráfico de función inversa se ve así:
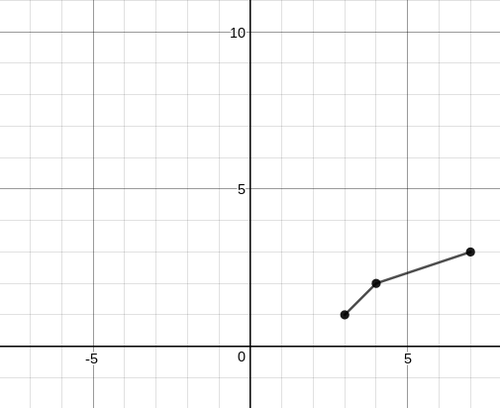
En este caso, el rango de la función tiene que restringirse para que sea 1 o mayor, de manera que la función inversa pase la prueba de línea vertical.
Estudia la siguiente gráfica y responde estas preguntas:
¿La relación graficada es una función?
¿La relación tiene una inversa que es una función?
Solución
El gráfico representa una función uno a uno. Pasa tanto una prueba de línea vertical como una horizontal. El inverso sería una función.
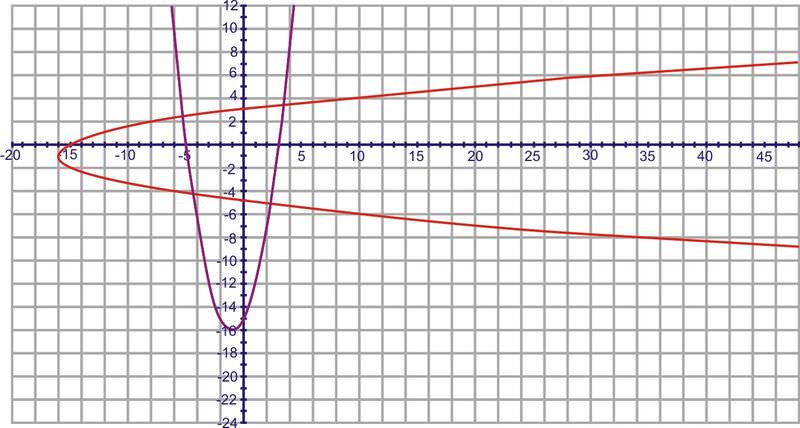
Encuentra la inversa de\(f(x)=x^2+2x−15\) usar el principio de mapeo.
Solución
Al seleccionar 4-5 puntos y cambiar los\(y\) valores\(x\) y, obtendrá la gráfica roja a continuación.
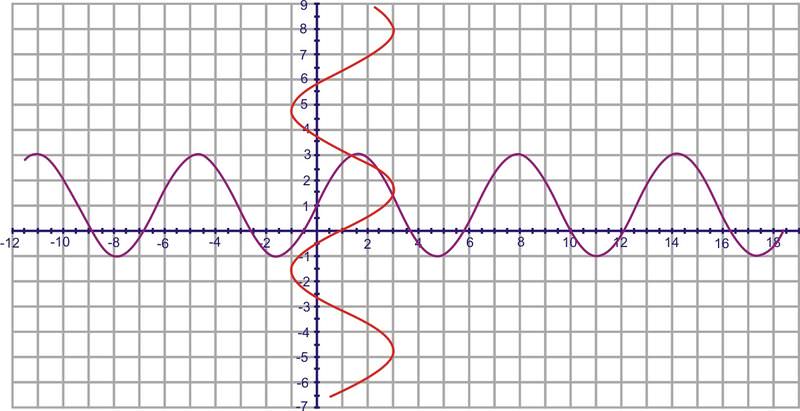
Encuentra la inversa de\(y=1+2 \sin x\) usar el principio de mapeo.
Solución
Al seleccionar 4-5 puntos y cambiar los\(y\) valores\(x\) y, obtendrá la gráfica roja a continuación.
Revisar
Para cada una de las siguientes gráficas responde estas preguntas:
a) ¿La relación graficada es una función?
b) ¿La relación tiene una inversa que es una función?
-
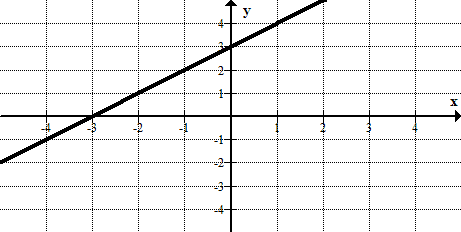
Figura\(\PageIndex{12}\) -
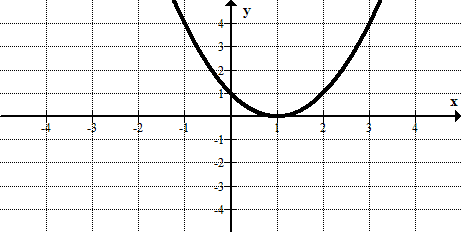
Figura\(\PageIndex{13}\) -
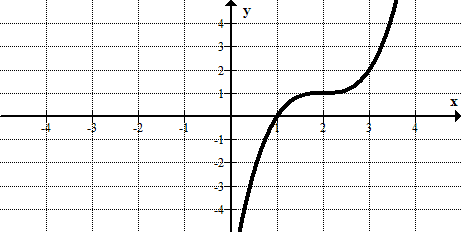
Figura\(\PageIndex{14}\) -
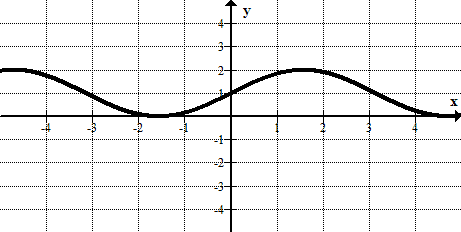
Figura\(\PageIndex{15}\) -
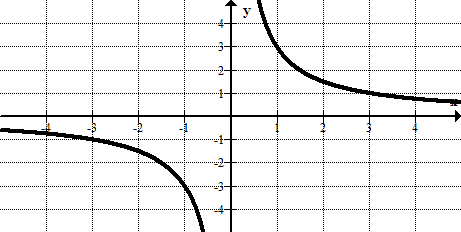
Figura\(\PageIndex{16}\) -
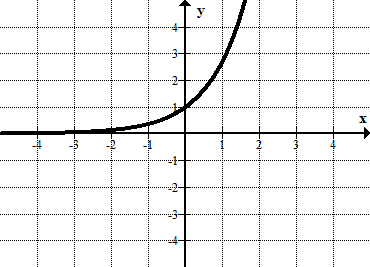
Figura\(\PageIndex{17}\)
Encuentra la inversa de cada función usando el principio de mapeo.
- \(y=x^2+x−2\)
- \(y=x^3\)
- \(y=\sin\left (x−\dfrac{\pi}{2}\right)\)
- \(y=\cos(2x)\)
- \(y=\dfrac{1}{x}\)
- \(y=x^2−9\)
- \(y=−2+\sin\left(\dfrac{1}{2}x\right)\)
- ¿Qué tipo de puntos estarán en el mismo lugar tanto en una función como en su inversa?
- Cuando graficas una función y su inversa en el mismo conjunto de ejes, ¿dónde está la línea de reflexión? ¿Por qué?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.4.
El vocabulario
| Término | Definición |
|---|---|
| función inversa | Las funciones inversas son funciones que se 'deshacen' entre sí. Formalmente\(f(x)\) y\(g(x)\) son funciones inversas si\(f(g(x))=g(f(x))=x\). |
| Mapeo | El mapeo es un procedimiento que implica el trazado de puntos en una cuadrícula de coordenadas para ver el comportamiento de una función. |