2.7.1: Graficar tangente, cotangente, secante y cosecante

Última actualización
Guardar como PDF

Page ID: 107666

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Gráficas tangentes, cotangentes, cosecantes y secantes. Mapa conceptual

Si ya conoces la relación entre la ecuación y la gráfica de las funciones seno y coseno entonces las otras cuatro funciones se pueden encontrar identificando ceros, asíntotas y puntos clave. ¿Las cuatro nuevas funciones son transformaciones de las funciones seno y coseno?

Graficando Otras Funciones Trigonométricas

Secante y Cosecante

Dado que la secante es la inversa del coseno, las gráficas están muy estrechamente relacionadas.

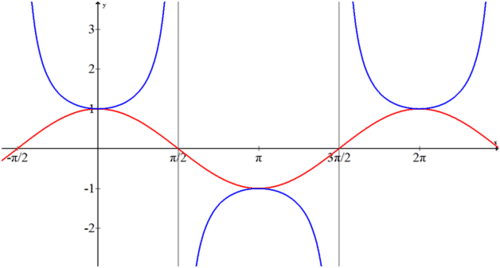
Observe donde sea que el coseno sea cero, la secante tiene una asíntota vertical y donde\(\cos x=1\) entonces\(\sec x=1\) también. Estas dos piezas lógicas permiten graficar cualquier función secante de la forma:

\(f(x)=\pm a\cdot \sec (b(x+c))+d\)

El método es graficarlo como lo harías con un coseno y luego insertar asíntotas y las curvas secantes para que toquen la curva coseno en sus valores máximo y mínimo. Esta técnica es idéntica a graficar gráficas cosecantes. Simplemente use la gráfica sinusoidal para encontrar la ubicación y las asíntotas.

Tangente y Cotangente

Las gráficas tangente y cotangente son más difíciles porque son una relación de las funciones seno y coseno.

\(\tan x=\dfrac{\sin x}{\cos x}\)
\(\cot x=\dfrac{\cos x}{\sin x}\)

La manera de pensar a través de la gráfica de\(f(x)=\tan x\) es determinar primero sus asíntotas. Las asíntotas ocurren cuando el denominador, coseno, es cero. Esto sucede en\(\pm \dfrac{\pi}{2}\),\(\pm \dfrac{3 \pi}{2}\)... Lo siguiente a trazar son los ceros que ocurren cuando el numerador, seno, es cero. Esto sucede en\(0,\pm \pi ,\pm ,2\pi \ldots\) Desde el círculo unitario y trigonometría básica del triángulo rectángulo, ya conoces algunos valores de\(\tan x\):

\(\tan \dfrac{\pi }{4}=1\)
\(\tan \left(−\dfrac{\pi }{4}\right)=−1\)

Al trazar toda esta información, se obtiene una muy buena idea de cómo se ve la gráfica de tangente y se puede rellenar el resto.

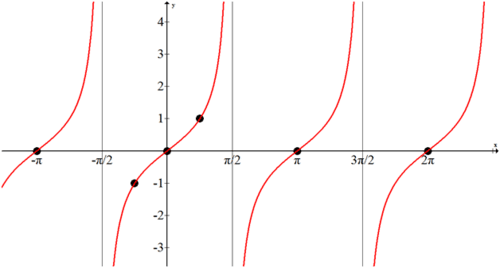
Observe que el periodo de tangente\(\pi \) no lo es\(2\pi \), porque tiene un ciclo más corto.

La gráfica de cotangente se puede encontrar usando lógica idéntica como tangente. Ya sabes\(\cot x=\dfrac{1}{\tan x}\). Esto significa que la gráfica de cotangente tendrá ceros dondequiera que la tangente tenga asíntotas y asíntotas donde la tangente tenga ceros. También sabes que donde la tangente es 1, la cotangente también es 1. Así, la gráfica de cotangente es:

Ejemplo\(\PageIndex{1}\)

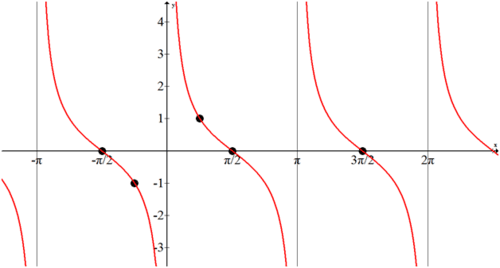
Anteriormente, se le preguntó si las cuatro nuevas funciones son transformaciones de seno y coseno.

Solución

Las cuatro nuevas funciones no son puramente transformaciones de las funciones seno y coseno. Sin embargo, secante y cosecante son transformaciones entre sí al igual que tangente y cotangente.

Ejemplo\(\PageIndex{2}\)

Grafica la función\(f(x)=−2\cdot \csc (\pi (x−1))+1\).

Solución

Grafica la función como si se tratara de una función sinusoidal. Luego inserte asíntotas donde la función sinusoidal cruce el eje sinusoidal. Por último añadir en las curvas cosecantes.

La amplitud es 2. La forma es seno negativo. La función se desplaza hacia arriba una unidad y hacia la derecha una unidad.

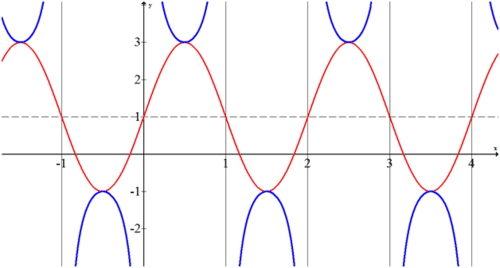
Tenga en cuenta que solo la porción azul de la gráfica representa la función dada.

Ejemplo\(\PageIndex{3}\)

¿Cómo se escribe una función tangente como una función cotangente?

Solución

Hay dos formas principales de ir entre una función tangente y una función cotangente. El primer método se discutió en el Ejemplo A:\(f(x)=\tan x=\dfrac{1}{\cot x}\).

El segundo enfoque implica dos transformaciones. Comience reflexionando a través del eje x o el eje y. Observe que esto produce un resultado idéntico. A continuación desplaza la función hacia la derecha o hacia la izquierda por\(\dfrac{\pi}{2}\). Nuevamente esto produce un resultado idéntico.

\(f(x)=\tan x=−\cot \left(x−\dfrac{\pi}{2}\right)\).

Ejemplo\(\PageIndex{4}\)

Encuentra la ecuación de la función en la siguiente gráfica.

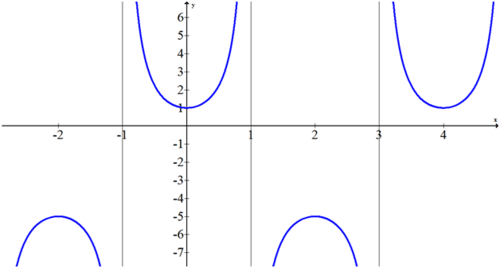
Solución

Si conecta los máximos y mínimos relativos de la función, produce una curva coseno desplazada con la que es más fácil trabajar.

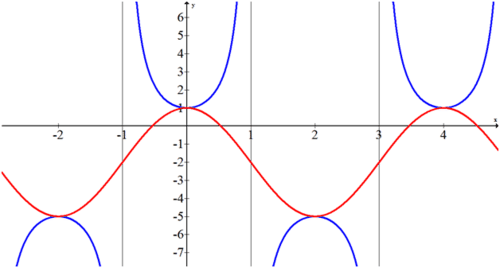
La amplitud es 3. El desplazamiento vertical es 2 hacia abajo. El periodo es 4 lo que implica que\(b=\dfrac{\pi}{2}\). La forma es coseno positivo y si eliges comenzar en x=0 no hay desplazamiento de fase.

\(f(x)=3\cdot \csc \left(\dfrac{\pi}{2}x\right)−2\)

Ejemplo\(\PageIndex{5}\)

¿Dónde están las asíntotas para tangentes y por qué ocurren?

Solución

Dado que\(\tan x=\dfrac{\sin x }{\cos x}\) las asíntotas ocurren siempre\(\cos x=0\) que sea\(\pm \dfrac{\pi}{2},\pm \dfrac{3 \pi}{2}, \ldots\)

Revisar

1. ¿Qué función puedes usar para ayudarte a hacer un boceto\(f(x)=\sec x\)? ¿Por qué?

2. ¿Qué función puedes usar para ayudarte a hacer un boceto\(g(x)=\csc x\)? ¿Por qué?

Haz un boceto de cada uno de los siguientes de memoria.

\(f(x)=\sec x\)
\(g(x)=\csc x\)
\(h(x)=\tan x\)
\(k(x)=\cot x\)

Grafica cada una de las siguientes.

\(f(x)=2\csc (x)+1\)
\(g(x)=2\csc (\dfrac{\pi}{2}x)+1\)
\(h(x)=2\csc \left(\dfrac{\pi }{2}(x−3)\right)+1\)
\(j(x)=\cot \left(\dfrac{\pi }{2}x\right)+3\)
\(k(x)=−\sec \left(\dfrac{\pi }{3}(x+1)\right)−4\)
\(m(x)=−\tan (x)+1\)
\(p(x)=−2\tan \left(x−\dfrac{\pi }{2}\right)+1\)
Encuentra dos formas de escribir\(\sec x\) en términos de otras funciones trigonométricas.
Encuentra dos formas de escribir\(\csc x\) en términos de otras funciones trigonométricas.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque\ sec ción 5.7.

El vocabulario

Término	Definición
asíntotas	Una asíntota es una línea en la gráfica de una función que representa un valor hacia el que la función puede acercarse, pero no alcanza (con ciertas excepciones).
Cosecante	El cosecante de un ángulo en un triángulo rectángulo es una relación que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado opuesto al ángulo dado. Este es el recíproco de la función sinusoidal.
Cotangente	La cotangente de un ángulo en un triángulo rectángulo es una relación que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud del lado opuesto al ángulo dado. Este es el recíproco de la función tangente.
Secante	La secante de un ángulo en un triángulo rectángulo es el valor que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado adyacente al ángulo dado. La relación secante es la recíproca de la relación coseno.
Transformaciones	Las transformaciones se utilizan para cambiar la gráfica de una función padre en la gráfica de una función más compleja.
Asíntota vertical	Una asíntota vertical es una línea vertical que marca un valor específico hacia el que puede acercarse la gráfica de una función, pero nunca alcanzará.

Recursos adicionales

Video: Gráficas de funciones cosecantes y secantes - Descripción general

Práctica: Graficar tangente, cotangente, secante y cosecante