2.7.6: Funciones trigonométricas inversas de la gráfica

Dominio y rango de funciones inversas.

Para que las inversas de funciones sean funciones, la función original debe pasar la prueba de línea horizontal. Aunque ninguna de las funciones trigonométricas pasa la prueba de línea horizontal, puede restringir sus dominios para que puedan pasar. Entonces los inversos se producen igual que con las funciones normales. Una vez que se tienen las funciones inversas básicas, se aplican las reglas de transformación normales.

¿Por qué es\(\sin^{-1}\left(\sin 370^{\circ}\right)\neq 370^{\circ}\)? ¿No cancelan el arcsin y el pecado?

Gráficas de funciones trigonométricas inversas

Dado que ninguna de las seis funciones trigonométricas pasa la prueba de línea horizontal, debe restringir sus dominios antes de encontrar inversos de estas funciones. Esto es igual que la forma\(y=\sqrt{x}\) es la inversa de\(y=x^2\) cuando restringes el dominio a\(x\geq 0\).

Considera la gráfica sinusoidal:

Figura\(\PageIndex{1}\)

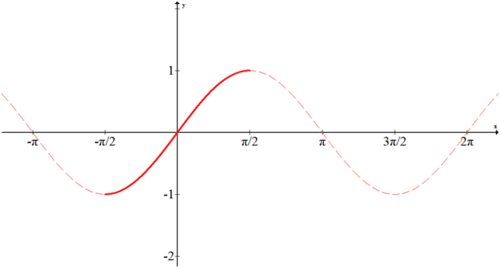
Como regla general, las restricciones al dominio son o bien el intervalo\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\) o\([0,\pi ]\) para mantener las cosas simples. En este caso el seno se restringe a\(\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]\), como se muestra arriba. Para encontrar la inversa, refleje la porción en negrita a través de la línea\(y=x\). La curva azul que aparece a continuación muestra\(f(x)=\sin^{-1}x\).

Figura\(\PageIndex{2}\)

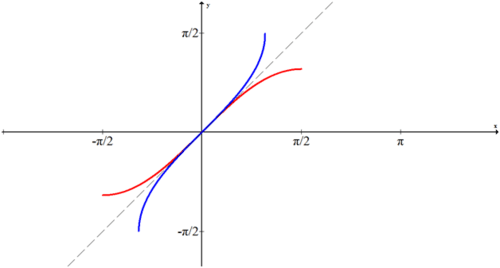
El resultado de esta inversión es que el arcoseno solo producirá ángulos entre\(−\dfrac{\pi}{2}\) y\(\dfrac{\pi}{2}\).

La curva azul de abajo muestra\(f(x)=\cos^{-1} x\)?

Figura\(\PageIndex{3}\)

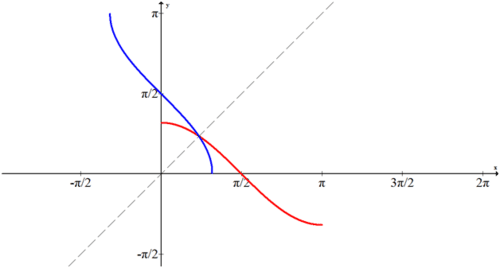
La porción de coseno que se ajusta a la prueba de línea horizontal es el intervalo\([0, \pi ]\). Para encontrar la inversa, esa porción se refleja a través de la línea\(y=x\).

Ejemplo\(\PageIndex{1}\)

Antes, se le preguntó por qué seno y arcoseno no siempre simplemente cancelan.

Solución

Dado que arcsine solo produce ángulos entre\(−\dfrac{\pi}{2}\) y\(\dfrac{\pi}{2}\) o\(−90^{\circ}\)\(+90^{\circ}\) al resultado de\(\sin^{-1}(\sin 370^{\circ})\) es\(10^{\circ}\) que es coterminal a\(370^{\circ}\).

Ejemplo\(\PageIndex{2}\)

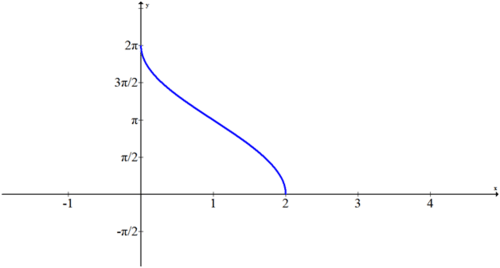
Grafica la función\(f(x)=2\cos^{-1}(x−1)\).

Solución

Ya que\(f(x)=\cos^{-1}x\) se graficó antes, ahora solo necesitas desplazarlo a la derecha una unidad y estirarlo verticalmente por un factor de 2. Intersectó el eje x en 1 antes y ahora se cruzará en 2. Alcanzó una altura de\(\pi \) antes y ahora alcanzará una altura de\(2\pi \).

Figura\(\PageIndex{4}\)

Ejemplo\(\PageIndex{3}\)

Evalúe la siguiente expresión con y sin calculadora utilizando triángulos rectos y su conocimiento de las funciones trigonométricas inversas.

\(\cot\left(\csc^{-1}\left(-\dfrac{13}{5}\right)\right)\)

Solución

Para poder calcular esto de manera efectiva es mejor escribir la expresión explícitamente solo en términos de funciones que su calculadora sí tiene. Tenga en cuenta que algunas calculadoras tienen ambos\(\sin^{-1}x\) y\((\sin x)^{−1}\).

La parte más difícil de esta pregunta es ver el csc como una función (que produce un ángulo) en una relación de una hipotenusa de 13 y un lado opuesto de -5. El seno de la relación inversa debe producir el mismo ángulo, por lo que puedes sustituirlo.

• \(\csc^{-1}\left(-\dfrac{13}{5}\right)=\sin^{-1}(−\dfrac{5}{13})\)
• \(\cot(\theta )=\dfrac{1}{\tan\theta}\)

\(\cot\left(\csc^{-1}\left(-\dfrac{13}{5}\right)\right)=\dfrac{1}{\tan \left(\sin^{-1}\left(−\dfrac{5}{13}\right)\right)}=−\dfrac{12}{5}\)

Comienza con tu conocimiento que\(\csc^{-1}\left(-\dfrac{13}{5}\right)\) describe un ángulo en el tercer o cuarto cuadrante porque esos son los dos cuadrantes donde el cosecante es negativo. Ya que\(\csc^{-1}\theta \) tiene rango\(−\dfrac{\pi}{2},\dfrac{\pi}{2}\), solo produce ángulos en el cuadrante I o en el cuadrante IV. Este triángulo debe entonces estar en el cuarto cuadrante. Todo lo que necesitas hacer es dibujar el triángulo e identificar la relación cotangente.

Figura\(\PageIndex{5}\)

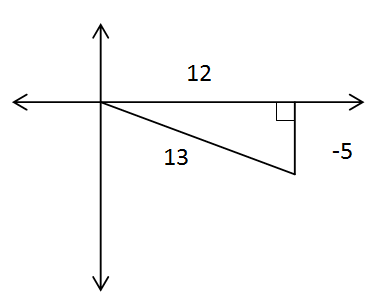
La cotangente es adyacente sobre el opuesto.

\(\cot\left(\csc^{-1}\left(−\dfrac{13}{5}\right)\right)=−\dfrac{12}{5}\)

Ejemplo\(\PageIndex{4}\)

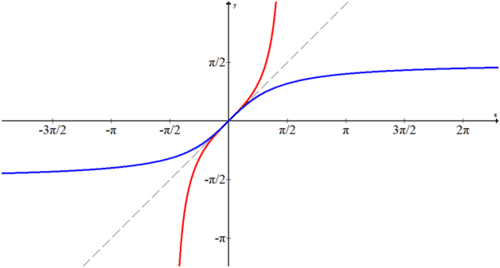
¿Cuál es la gráfica\(y=\tan^{-1}x\)?

Solución

Grafique la porción de tangente que se ajuste a la prueba de línea horizontal y refleje a través de la línea y=x Tenga en cuenta que la gráfica de arctan está en azul.

Figura\(\PageIndex{6}\)

Ejemplo\(\PageIndex{5}\)

¿Cuál es la gráfica de\(y=\csc^{-1}x\)

Solución

Grafique la porción de cosecante que se ajuste a la prueba de línea horizontal y refleje a través de la línea y=x.

Figura\(\PageIndex{7}\)

Figura\(\PageIndex{8}\)

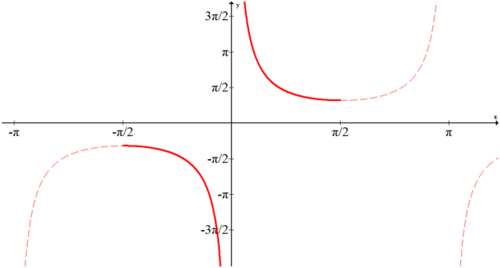
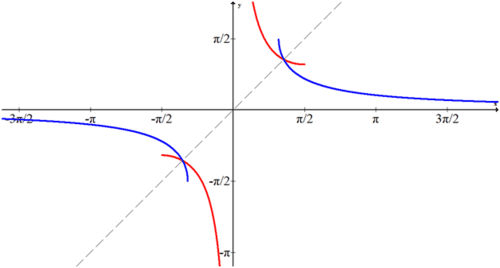
Tenga en cuenta que\(f(x)=\csc^{-1}x\) está en azul.

Revisar

1. Gráfica\(f(x)=\cot^{-1}x\).
2. Gráfica\(g(x)=\sec^{-1}x\).

Nombra cada una de las siguientes gráficas.

3. 

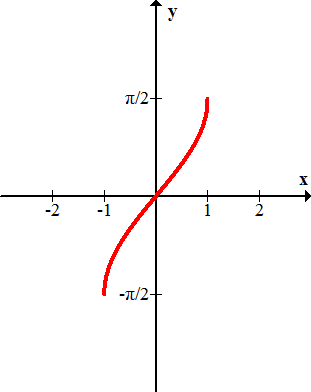
   Figura\(\PageIndex{8}\)

4. 

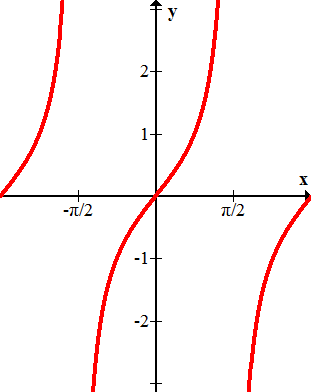
   Figura\(\PageIndex{9}\)

5. 

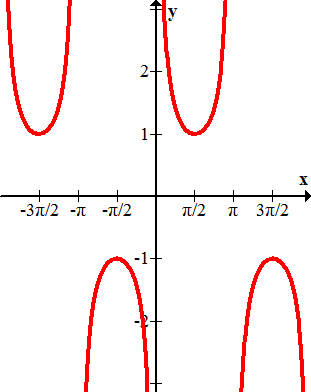
   Figura\(\PageIndex{10}\)

6. 

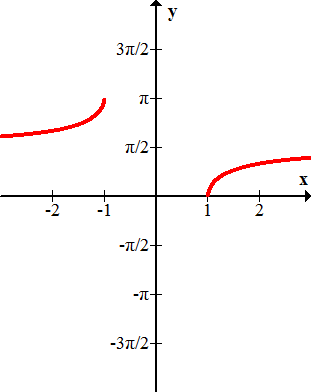
   Figura\(\PageIndex{11}\)

7. 

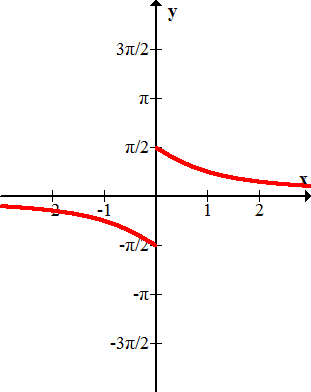
   Figura\(\PageIndex{12}\)

Grafique cada una de las siguientes funciones utilizando su conocimiento de las transformaciones de funciones.

8. \(h(x)=3\sin^{-1}(x+1)\)
9. \(k(x)=2\sin^{-1}(x)+\dfrac{\pi}{2}\)
10. \(m(x)=−\cos^{-1}(x−2)\)
11. \(j(x)=\cot^{-1}(x)+\pi\)
12. \(p(x)=−2\tan^{-1}(x−1)\)
13. \(q(x)=\csc^{-1}(x−2)\)
14. \(r(x)=−\sec^{-1}(x)+4\)
15. \(t(x)=\csc^{-1}(x+1)−\dfrac{3 \pi}{2}\)
16. \(v(x)=2\sec^{-1}(x+2)+\dfrac{\pi}{2}\)
17. \(w(x)=−\cot^{-1}(x)−\dfrac{\pi}{2}\)

Evaluar cada expresión.

18. \(\sec \left(\tan^{-1}\left[\dfrac{3}{4}\right]\right)\)
19. \(\cot \left(\csc^{-1} \left[\dfrac{13}{12}\right]\right)\)
20. \(\csc \left(\tan^{-1} \left[\dfrac{4}{3}\right]\right)\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.8.

El vocabulario

Término	Definición
Cosecante	El cosecante de un ángulo en un triángulo rectángulo es una relación que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado opuesto al ángulo dado. Este es el recíproco de la función sinusoidal.
Cotangente	La cotangente de un ángulo en un triángulo rectángulo es una relación que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud del lado opuesto al ángulo dado. Este es el recíproco de la función tangente.
Coterminal	Dos ángulos son coterminales si se dibujan en la posición estándar y ambos tienen lados terminales que están en la misma ubicación.
dominio	El dominio de una función es el conjunto de valores x para los que se define la función.
Prueba de Línea Horizontal	La prueba de línea horizontal dice que si una línea horizontal dibujada en cualquier lugar a través del gráfico de una función intersecta a la función en más de una ubicación, entonces la función no es uno a uno y no es invertible.
dominio restringido	Dominio restringido se refiere al hecho de que al crear una inversa a veces se debe cortar el dominio de la mayor parte de la función, guardando la mayor porción posible para que cuando se crea la inversa también sea una función.
Secante	La secante de un ángulo en un triángulo rectángulo es el valor que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado adyacente al ángulo dado. La relación secante es la recíproca de la relación coseno.
Transformaciones	Las transformaciones se utilizan para cambiar la gráfica de una función padre en la gráfica de una función más compleja.

Recursos adicionales

Práctica: Funciones trigonométricas inversas gráficas