4.1.1: Leyes de los senos y cosenos
- Page ID
- 107643
Resolviendo partes de triángulos no rectos mediante trigonometría.
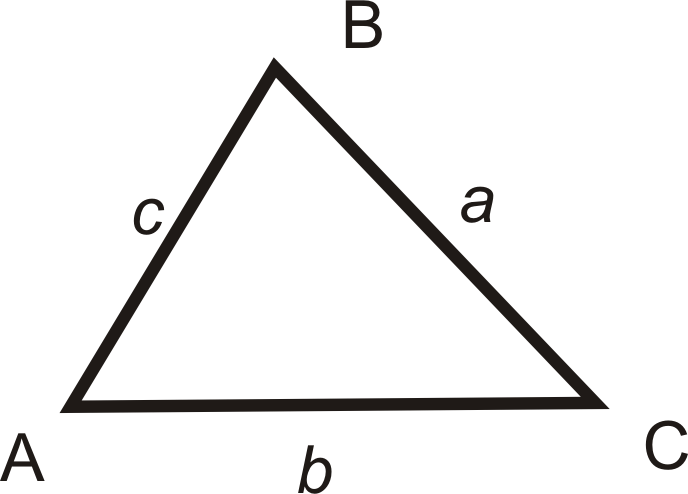
Ley de los senos: Si\(\Delta ABC\) tiene lados de longitud,\(a\),\(b\), y\(c\), entonces\(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\).
Al mirar un triángulo, las longitudes a, b y c son opuestas a los ángulos de la misma letra.
Use la Ley de Senos cuando se le dé:
- Un ángulo y su lado opuesto.
- Dos ángulos cualesquiera y un lado.
Dos lados y el ángulo no incluido.
Ley de Cosinos: Si\(\Delta ABC\) tiene lados de longitud\(a\),\(b\), y\(c\), entonces:
\(\begin{aligned} a^2&=b^2+c^2−2bc\cos A \\ b^2&=a^2+c^2−2ac \cos B \\ c^2&=a^2+b^2−2ab \cos C \end{aligned}\)
A pesar de que hay tres fórmulas, todas son muy similares. Primero, observe que cualquiera que sea el ángulo que esté en el coseno, el lado opuesto está en el otro lado del signo igual.
Ley de Uso de Cosinos cuando se le da:
- Dos lados y el ángulo incluido.
- Los tres lados.
Uso de la Ley de los Sines
1. Resuelve el triángulo usando la Ley de Sines. Respuestas decimales redondas al décimo más cercano.
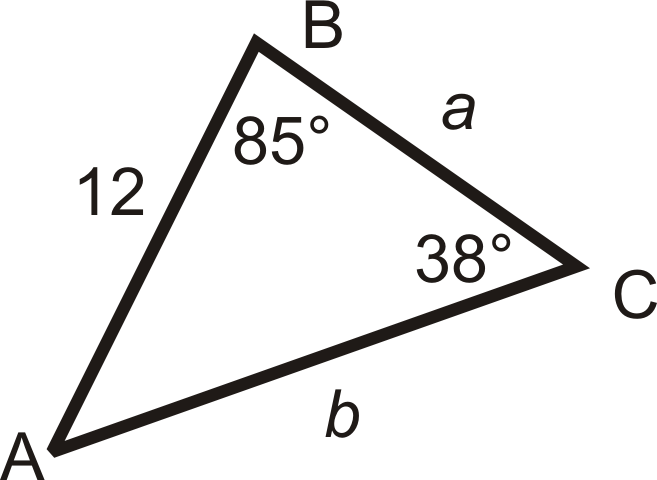
Primero, para encontrar\(m\angle A\), podemos usar el Teorema de la Suma del Triángulo.
\(\begin{aligned} m\angle A+85^{\circ} +38^{\circ}&=180^{\circ} \\ m\angle A&=57^{\circ} \end{aligned}\)
Ahora, usa la Ley de los Sinos para establecer ratios para\(a\) y\(b\).
\(\dfrac{\sin 57^{\circ} }{a}=\dfrac{\sin 85^{\circ} }{b}=\dfrac{\sin 38^{\circ} }{12}\)
\ (\ begin {alineado}
\ dfrac {\ sin 57^ {\ circ}} {a} &=\ dfrac {\ sin 38^ {\ circ}} {12} &\ dfrac {\ sin 85^ {\ circ}} {b} &=\ dfrac {\ sin 38^ {\ circ}} {12}\\
a\ cdot\ sin 38^ {\ circ} &=12\ cdot\ sin 57^ {\ circ} & b\ cdot\ sin 38^ {\ circ} &=12\ cdot\ sin 85^ {\ circ}\\
a &=\ dfrac {12\ cdot\ sin 57^ {\ circ}} {\ sin 38^ {\ circ}}\ aprox 16.4 &\ quad b &=\ dfrac {12\ cdot\ sin 85^ {\ circ}} {\ sin 38^ {\ circ}}\ aproximadamente 19.4
\ final {alineado}\)
2. Resuelve el triángulo usando la Ley de Sines. Respuestas decimales redondas al décimo más cercano.
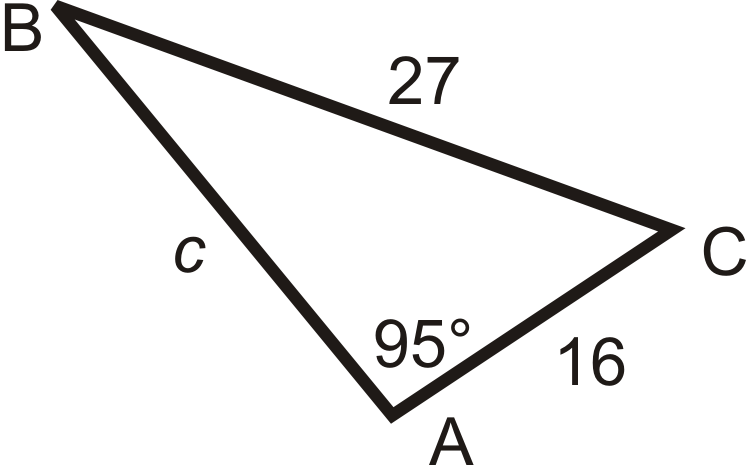
Establecer la relación para el\(\angle B\) uso de Ley de Sines.
\(\begin{aligned} \dfrac{\sin 95^{\circ} }{27}&=\dfrac{\sin B}{16} \\ 27\cdot \sin B&=16\cdot \sin 95^{\circ} \\ \sin B&=\dfrac{16\cdot \sin 95^{\circ} }{27}\rightarrow\sin ^{−1}\left(\dfrac{16\cdot \sin 95^{\circ} }{27} \right) =36.2^{\circ} \end{aligned}\)
Para encontrar\(m\angle C\) utilizar el Teorema de la suma del triángulo.
\(m\angle C+95^{\circ} +36.2^{\circ} =180^{\circ} \rightarrow m\angle C=48.8^{\circ}\)
Para encontrar\(c\), utilizar de nuevo la Ley de los Sines. \(\dfrac{\sin 95^{\circ} }{27}=\dfrac{\sin 48.8^{\circ} }{c}\)
\(\begin{aligned} c\cdot \sin 95^{\circ}&=27\cdot \sin 48.8^{\circ} \\ c&=27\cdot \sin 48.8^{\circ} \sin 95^{\circ} \approx 20.4 \end{aligned}\)
Uso de la Ley de Cosinos
Resuelve el triángulo usando Ley de Cosinos. Redondee sus respuestas a la centésima más cercana.
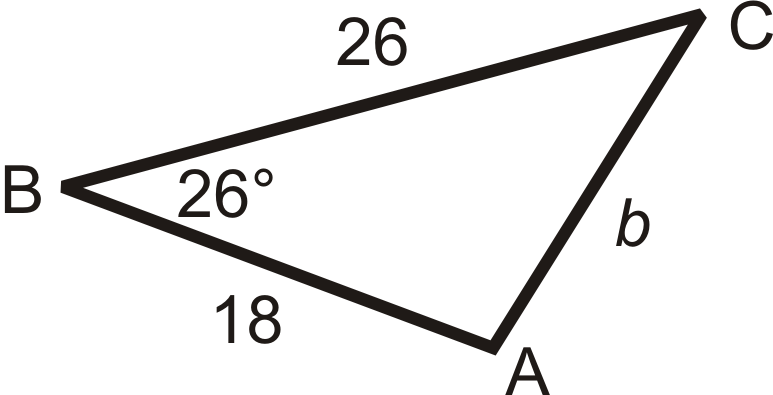
Usa la segunda ecuación para resolver\(\angle B\).
\(\begin{aligned} b^2&=26^2+18^2−2(26)(18)\cos 26^{\circ} \\ b^2&=1000−936\cos 26^{\circ} \\ b^2&=158.7288 \\ b&\approx 12.60 \end{aligned}\)
Para encontrar\(m\angle A\) o\(m\angle C\), se puede utilizar ya sea la Ley de los Senos o la Ley de Cosinos. Usemos la Ley de los Senos.
\(\begin{aligned} \dfrac{\sin 26^{\circ} }{12.60}&=\dfrac{\sin A}{18} \\ 12.60\cdot \sin A&=18\cdot \sin 26^{\circ} \\ \sin A&=18\cdot \sin 26^{\circ} 12.60 \end{aligned}\)
\(\sin ^{−1} \left(18\cdot \sin 26^{\circ} 12.60 \right)\approx 38.77^{\circ} \)Para encontrar\(m\angle C\), usa el Teorema de la suma del triángulo.
\(\begin{aligned} 26^{\circ} +38.77^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=115.23^{\circ} \end{aligned}\)
Ejemplos
Encuentra los siguientes ángulos en el triángulo de abajo. Redondee sus respuestas a la centésima más cercana.
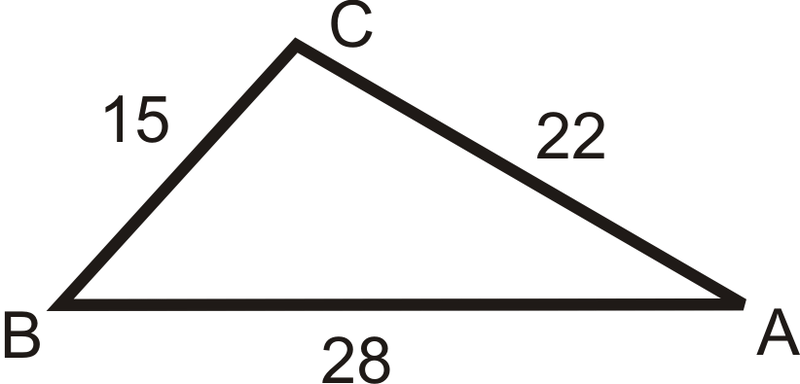
\(m\angle A\)
Solución
Cuando te dan solo los lados, tienes que usar la Ley de los Cosinos para encontrar un ángulo y luego puedes usar la Ley de los Sinos para encontrar otro.
\(\begin{aligned} 15^2&=22^2+28^2−2(22)(28)\cos A \\ 225&=1268−1232\cos A \\ −1043&=−1232\cos A \\ \dfrac{−1043}{−1232}&=\cos A \rightarrow \cos ^{−1}\left(\dfrac{1043}{1232}\right) \approx 32.16^{\circ}\end{aligned}\)
\(m\angle B\)
Solución
Ahora que tenemos un ángulo y su lado opuesto, podemos usar la Ley de los Sinos.
\(\begin{aligned} \dfrac{\sin 32.16^{\circ} }{15} &=\dfrac{\sin B}{22} \\ 15\cdot \sin B &=22\cdot \sin 32.16^{\circ} \\ \sin B &=\dfrac{22\cdot \sin 32.16^{\circ} }{15} \end{aligned}\)
\(\sin ^{−1}\left(\dfrac{22\cdot \sin 32.16^{\circ} }{15}\right)\approx 51.32^{\circ} \).
\(m\angle C\)
Solución
Para encontrar\(m\angle C\), usa el Teorema de la suma del triángulo.
\(\begin{aligned} 32.16^{\circ} +51.32^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=96.52^{\circ} \end{aligned}\)
Revisar
Utilizar la Ley de Senos o Cosinos para resolver\(\Delta ABC\). Si no te dan una imagen, dibuja una. Redondear todas las respuestas decimales a la décima más cercana.
-
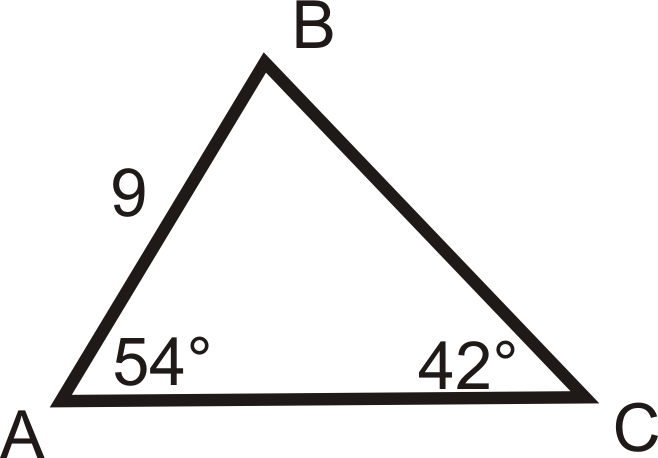
Figura\(\PageIndex{6}\) -
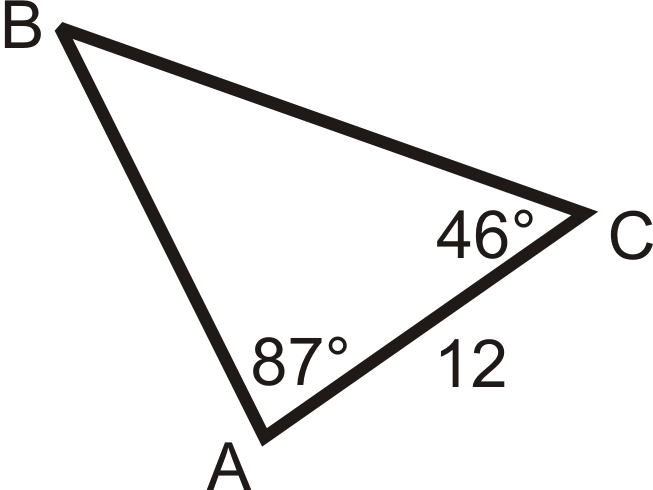
Figura\(\PageIndex{7}\) -
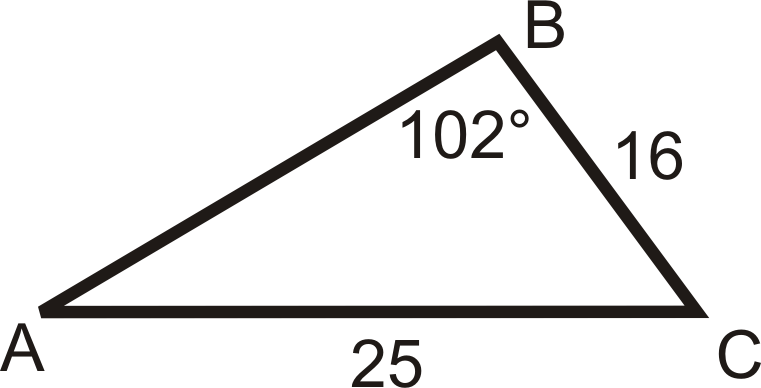
Figura\(\PageIndex{8}\) -
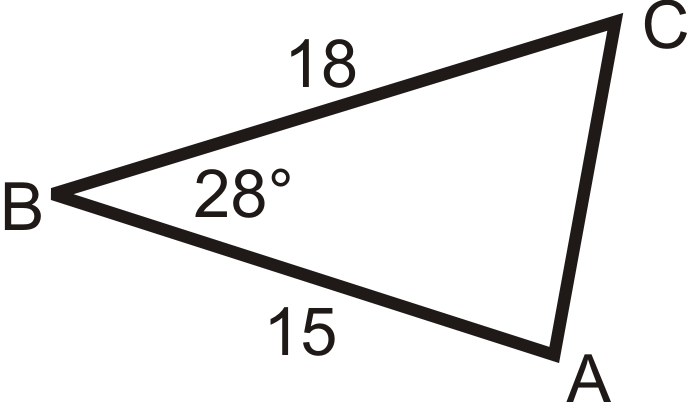
Figura\(\PageIndex{9}\) -
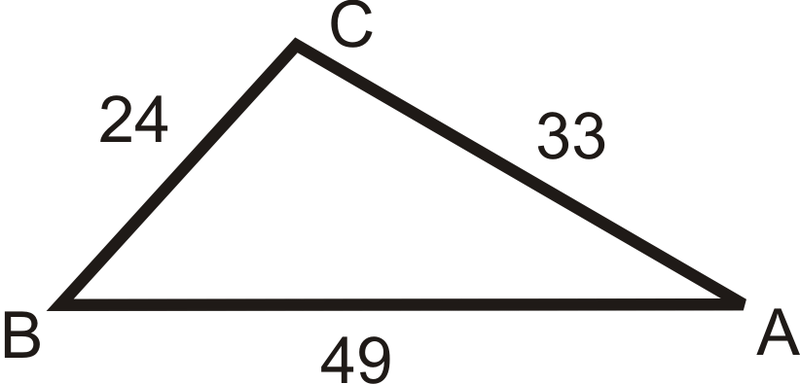
Figura\(\PageIndex{10}\) -
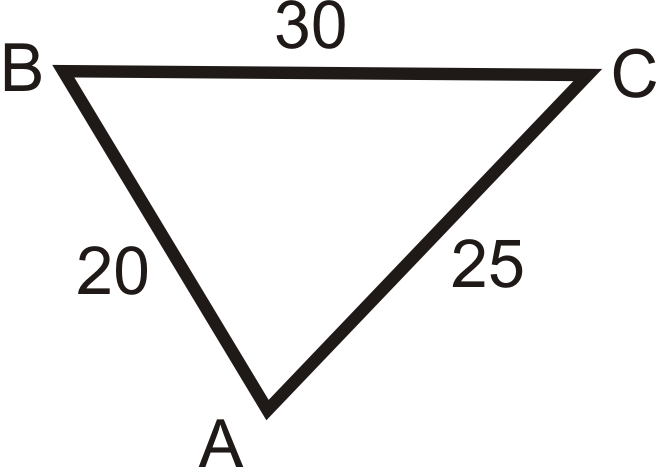
Figura\(\PageIndex{11}\) -
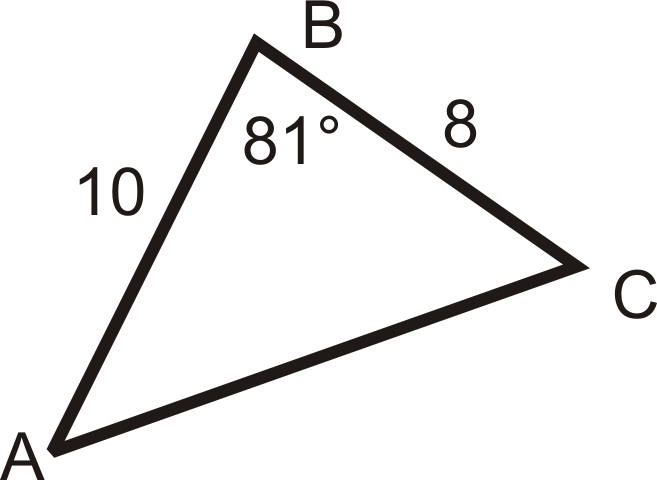
Figura\(\PageIndex{12}\) -
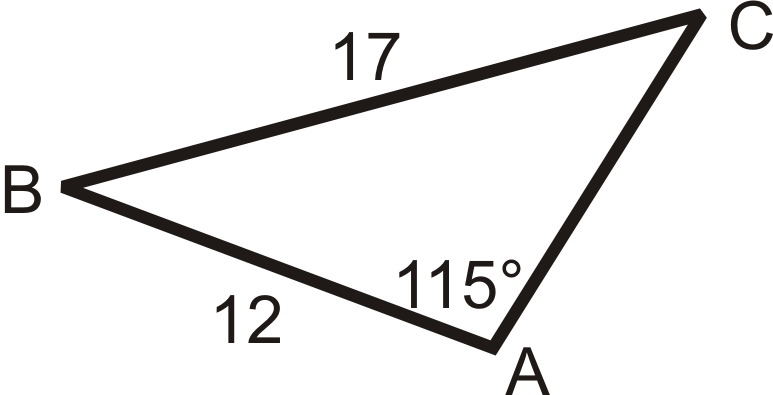
Figura\(\PageIndex{13}\) -
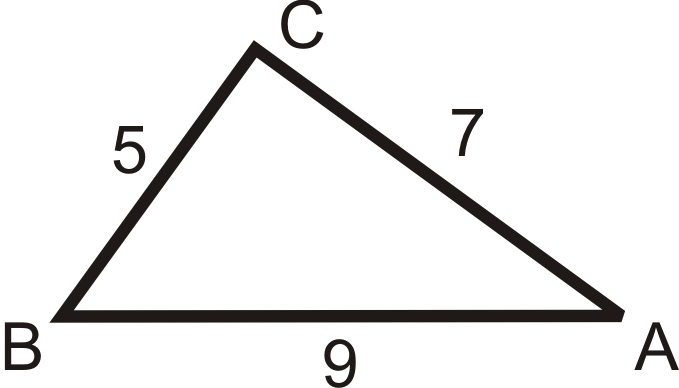
Figura\(\PageIndex{14}\) - \(m\angle A=74^{\circ} \),\(m\angle B=11^{\circ} \),\(BC=16\)
- \(m\angle A=64^{\circ} \),\(AB=29\),\(AC=34\)
- \(m\angle C=133^{\circ} \),\(m\angle B=25^{\circ} \),\(AB=48\)
Usa la Ley de Sinos para resolver a\(\Delta ABC\) continuación.
- \(m\angle A=20^{\circ} \),\(AB=12\),\(BC=5\)
Recordemos que cuando aprendimos a probar que los triángulos eran congruentes determinamos que SSA (dos lados y un ángulo no incluido) no determinaba un triángulo único. Cuando estamos usando la Ley de Sines para resolver un triángulo y se nos dan dos lados y el ángulo no incluido, es posible que tengamos dos triángulos posibles. El problema 14 ilustra esto.
- Digamos que tenemos\(\Delta ABC\) como lo hicimos en el problema 13. En el problema 13 te dieron dos lados y el ángulo no incluido. Esta vez, tienes dos ángulos y el lado entre ellos (ASA). Resolver el triángulo dado que\(m\angle A=20^{\circ} \),\(m\angle C=125^{\circ}\),\(AC=8.4\)
- ¿El triángulo que encontraste en el problema 14 cumple con los requisitos de la información dada en el problema 13? ¿En qué se\(m\angle C\) relacionan los dos diferentes? Dibuja los dos posibles triángulos superpuestos para visualizar esta relación.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.10.

