4.1.3: Triángulos ángulo-ángulo-lateral
- Page ID
- 107619
Ley de los senos: proporción basada en proporciones de lados y senos de ángulos opuestos.
Tú y un amigo deciden ir a volar cometas en una ventosa tarde de sábado. Mientras estás sentado para hacer tus cometas, estás trabajando en hacer la mejor forma posible para atrapar la brisa. Mientras tu amigo decide ir con una cometa en forma de diamante, intentas hacer una en forma de triángulo. Mientras intentas pegar la cometa, haces que la primera y la segunda pieza se traben con un\(70^{\circ} \) ángulo. El ángulo entre la primera y tercera piezas es\(40^{\circ} \). Por último, también has medido la longitud de la segunda pieza y has encontrado que es de 22 pulgadas de largo.
Tu cometa se ve así:
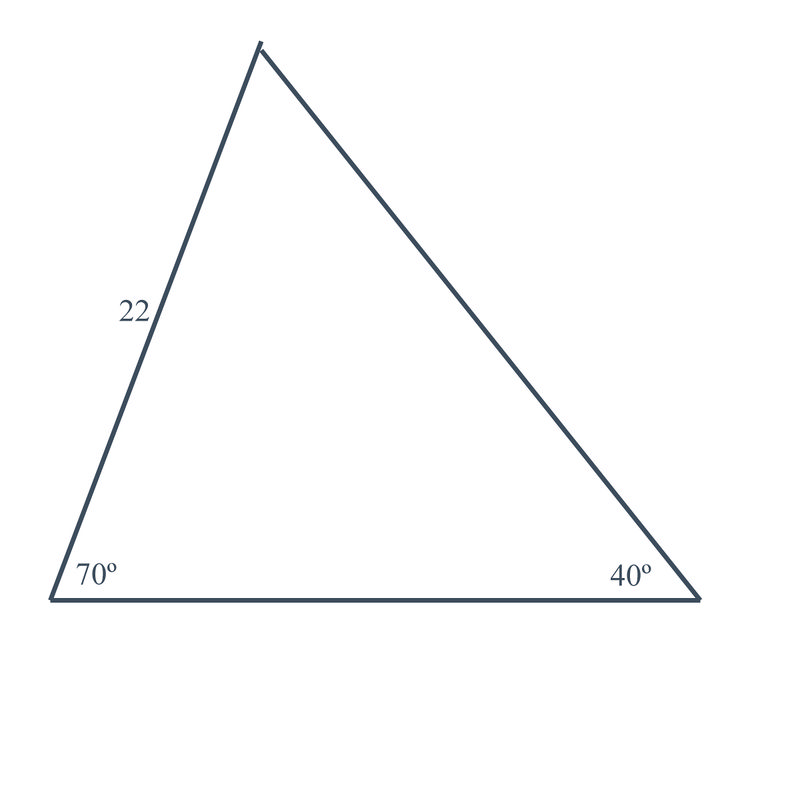
¿Hay alguna manera de averiguar, usando las matemáticas, cuál será la longitud del tercer lado?
Triángulos AAS
La Ley de los senos establece:\(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}\). Esta es una relación entre el seno de un ángulo en un triángulo y la longitud del lado opuesto a ese ángulo al seno de un ángulo diferente en ese triángulo y la longitud del lado opuesto a ese segundo ángulo.
La Ley de los senos nos permite encontrar muchas cantidades de interés en los triángulos comparando lados y ángulos interiores como una relación. Un caso en el que podemos usar la Ley de los senos es cuando conocemos dos de los ángulos en un triángulo y un lado no incluido (AAS).
Usando la Ley de los senos
1. utilizando\(\Delta GMN\),\(\angle G=42^{\circ} \),\(\angle N=73^{\circ} \) y\(g=12\). Encuentra\(n\).
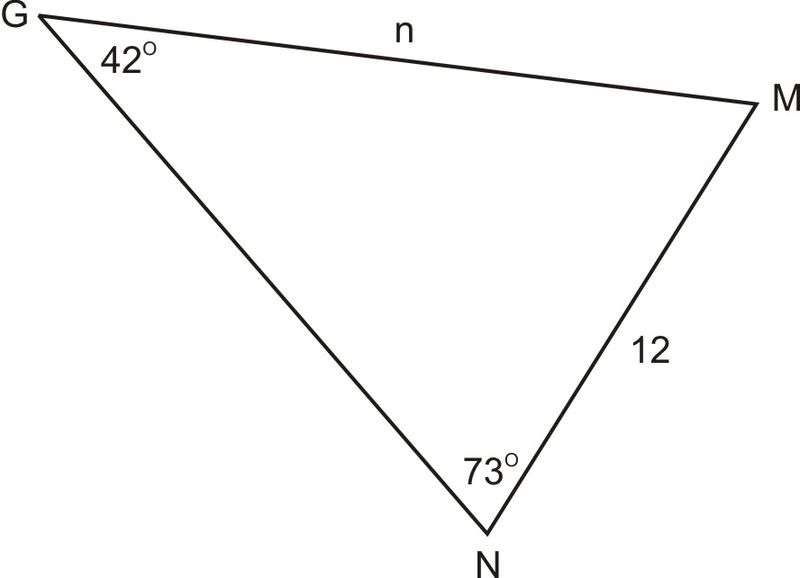
ya que conocemos dos ángulos y un lado no incluido (\(g\)), podemos encontrar el otro lado no incluido (\(n\)).
\(\begin{aligned} \dfrac{\sin 73^{\circ} }{n}&=\dfrac{\sin 42^{\circ} }{12} \\ n\sin 42^{\circ}&=12\sin 73^{\circ} \\ n&=\dfrac{12\sin 73^{\circ} }{\sin 42^{\circ} } \\ n&\approx 17.15 \end{aligned}\)
2. Continuando desde #1, encontrar\(\angle M\) y\(m\).
\(\angle M\)es simplemente\(180^{\circ} −42^{\circ} −73^{\circ} =65^{\circ} \). Para encontrar lado\(m\), ahora puedes usar ya sea la Ley de los senos o la Ley de los Cosinos. Considerando que la Ley de los senos es un poco más simple y nueva, usémosla. No importa qué lado y ángulo opuesto uses en la proporción con\(\angle M\) y\(m\).
Opción 1:\(\angle G\) y\(g\)
\(\begin{aligned} \dfrac{\sin 65^{\circ} }{m}&=\dfrac{\sin 42^{\circ} }{12} \\ m\sin 42^{\circ}&=12\sin 65^{\circ} \\ m&=\dfrac{12\sin 65^{\circ} }{\sin 42^{\circ} } \\ m&\approx 16.25 \end{aligned}\)
Opción 2:\(\angle N\) y\(n\)
\(\begin{aligned} \dfrac{\sin 65^{\circ} }{m}&=\dfrac{\sin 73^{\circ} }{17.15} \\ m\sin 73^{\circ}&=17.15\sin 65^{\circ} \\ m&=\dfrac{17.15\sin 65^{\circ} }{\sin 73^{\circ} } \\ m &\approx 16.25 \end{aligned}\)
3. Un grupo empresarial quiere construir un campo de golf en un terreno que alguna vez fue una granja. La escritura de la tierra es antigua y la información sobre la tierra es incompleta. Si\(AB\) es 5382 pies,\(BC\) es 3862 pies,\(\angle AEB\) es\(101^{\circ} \),\(\angle BDC\) es\(74^{\circ}\),\(\angle EAB\) es\(41^{\circ} \) y\(\angle DCB\) es\(32^{\circ} \), ¿cuáles son las longitudes de los lados de cada pedazo triangular de tierra? ¿Cuál es la superficie total del terreno?
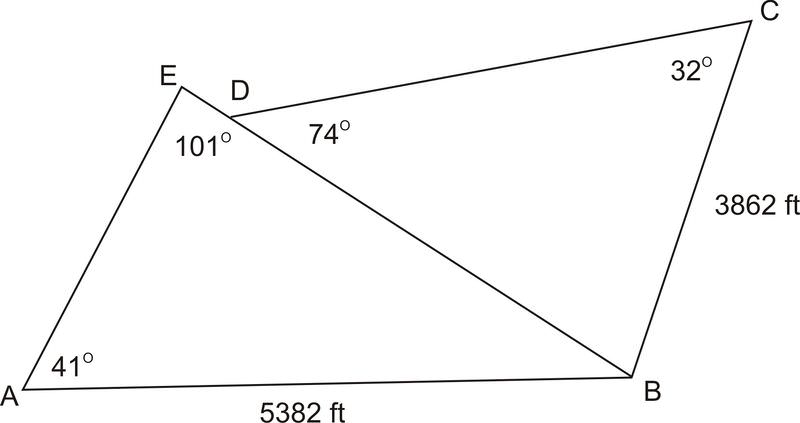
Antes de que podamos averiguar el área del terreno, necesitamos averiguar la longitud de cada lado. En\(\Delta ABE\), conocemos dos ángulos y un lado no incluido. Este es el caso de AAS. Primero, encontraremos el tercer ángulo adentro\(\Delta ABE\) usando el Teorema de la Suma del Triángulo. Entonces, podemos usar la Ley de los senos para encontrar ambos\(AE\) y\(EB\).
\ (\ comenzar {alineado}
\ dfrac {\ sin 101} {5382} &=\ dfrac {\ sin 38} {A E} &\ dfrac {\ sin 101} {5382} &=\ dfrac {\ sin 41} {E B}\\
A E (\ sin 101) &=5382 (\ sin 38) & E B (\ sin 101) &=5382 (\ sin 41)\\
A E &=\ dfrac {5382 (\ sin 38)} {\ sin 101} & E B&=\ dfrac { 5382 (\ sin 41)} {\ sin 101}\
A E &=3375.5\ texto {pies} & E B &\ aprox 3597,0\ texto {pies}
\ final {alineado}\)
A continuación, necesitamos encontrar las longitudes laterales faltantes en\(\Delta DCB\). En este triángulo, nuevamente conocemos dos ángulos y un lado no incluido (AAS), lo que significa que podemos usar la Ley de los senos. Primero, vamos a\(\angle DBC=180−(74+32)=74^{\circ} \) encontrar. ya que ambos\(\angle BDC\) y\(\angle DBC\) medir\(74^{\circ} \),\(\Delta DCB\) es un triángulo isósceles. Esto significa que dado que\(BC\) es 3862 pies, también\(DC\) es 3862 pies. Todo lo que nos queda por encontrar ahora es\(DB\).
\(\begin{aligned} \dfrac{\sin 74}{3862}&=\dfrac{\sin 32 }{DB}\\ DB(\sin 74)&=3862(\sin 32) \\ DB&=\dfrac{3862(\sin 32)}{\sin 74} \\ DB &\approx 2129.0 \text{ feet} \end{aligned}\)
Finalmente, necesitamos calcular el área de cada triángulo y luego sumar las dos áreas juntas para obtener el área total. De la última sección aprendimos dos fórmulas de área,\(K=\dfrac{1}{2} bc\sin A\) y la Fórmula de Heron. En este caso, ya que tenemos suficiente información para usar cualquiera de las dos fórmulas, la usaremos\(K=\dfrac{1}{2} bc\sin A\) ya que es menos intensa computacionalmente.
Primero, encontraremos la zona de\(\Delta ABE\).
\(\Delta ABE\):
\(\begin{aligned} K&=12(3375.5)(5382)\sin 41 \\ K&=5,959,292.8 \text{ ft}^2 \end{aligned}\)
\(\Delta DBC\):
\(\begin{aligned} K&=\dfrac{1}{2}(3862)(3862)\sin 32 \\ K&=3,951,884.6 \text{ ft}^2 \end{aligned}\)
El área total es\(5,959,292.8+3,951,884.6=9,911,177.4 \text{ ft}^2\).
Anteriormente, se le pidió que encontrara la longitud del tercer lado del triángulo.
Solución
ya que conoces dos ángulos y un lado no incluido de la cometa, puedes encontrar el otro lado no incluido usando la Ley de los senos. Establece una relación usando los ángulos y el lado que conoces y el lado que no conoces.
\(\begin{aligned} \dfrac{\sin 70^{\circ} }{x}&=\dfrac{\sin 40^{\circ} }{22} \\ x&=\dfrac{22 \sin 70^{\circ} }{\sin 40^{\circ} } \\ x &\approx 32.146 \end{aligned}\)
La longitud de la varilla del taco en el lado desconocido será de aproximadamente 32 pulgadas.
Encuentra el lado “d” en el triángulo de abajo con la siguiente información:\(e=214.9\),\(D=39.7^{\circ} \),\(E=41.3^{\circ}\)
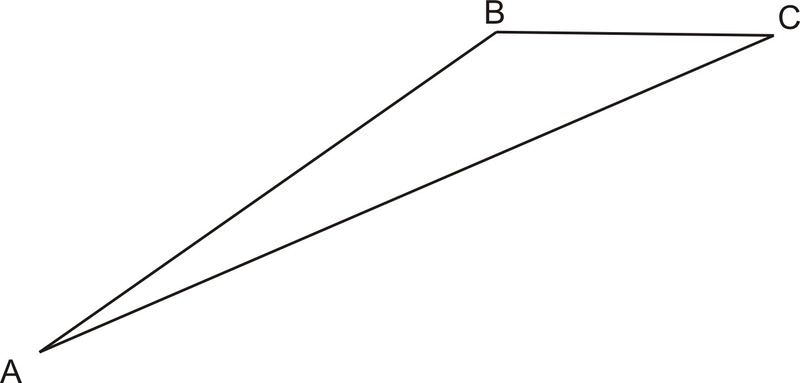
Solución
\(\dfrac{\sin 41.3^{\circ} }{214.9}=\dfrac{\sin 39.7^{\circ} }{d}\),\(d=208.0\)
Encuentra el lado “o” en el triángulo de abajo con la siguiente información:\(M=31^{\circ} \),\(O=9^{\circ} \),\(m=15\)

Solución
\(\dfrac{\sin 9^{\circ} }{o}=\dfrac{\sin 31^{\circ} }{15}\),\(o=4.6\)
Encuentra el lado “q” en el triángulo de abajo con la siguiente información:\(Q=127^{\circ} \),\(R=21.8^{\circ} \),\(r=3.62\)
Solución
\(\dfrac{\sin 127^{\circ} }{q}=\dfrac{\sin 21.8^{\circ} }{3.62}\),\(q=7.8\)
Revisar
En\(\Delta ABC\),\(m\angle A=50^{\circ}\),\(m\angle B=34^{\circ}\), y\(a=6\).
- Encuentra la longitud de\(b\).
- Encuentra la longitud de\(c\).
En\(\Delta KMS\),\(m\angle K=42^{\circ}\),\(m\angle M=26^{\circ}\), y\(k=14\).
- Encuentra la longitud de\(m\).
- Encuentra la longitud de\(s\).
En\(\Delta DEF\),\(m\angle D=52^{\circ}\),\(m\angle E=78^{\circ}\), y\(d=23\).
- Encuentra la longitud de\(e\).
- Encuentra la longitud de\(f\).
En\(\Delta PQR\),\(m\angle P=2^{\circ}\),\(m\angle Q=79^{\circ}\), y\(p=20\).
- Encuentra la longitud de\(q\).
- Encuentra la longitud de\(r\).
En\(\Delta DOG\),\(m\angle D=50^{\circ} \),\(m\angle G=59^{\circ} \), y\(o=12\).
- Encuentra la longitud de\(d\).
- Encuentra la longitud de\(g\).
En\(\Delta CAT\),\(m\angle C=82^{\circ}\),\(m\angle T=4^{\circ}\), y a=8\).
- Encuentra la longitud de c\).
- Encuentra la longitud de t\).
En\(\Delta YOS\),\(m\angle Y=65^{\circ}\),\(m\angle O=72^{\circ}\), y\(s=15\).
- Encuentra la longitud de\(o\).
- Encuentra la longitud de\(y\).
En\(\Delta HCO\),\(m\angle H=87^{\circ}\),\(m\angle C=14^{\circ}\), y\(o=19\).
- Encuentra la longitud de\(h\).
- Encuentra la longitud de\(c\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.7.
El vocabulario
| Término | Definición |
|---|---|
| Ángulo Ángulo Triángulo Lateral | Un 'triángulo de ángulo lateral' es un triángulo donde dos de los ángulos y el lado no incluido son cantidades conocidas. |
Recursos adicionales
Video: Ejemplo: Resolviendo un Triángulo usando la Ley de los senos Dados Dos Ángulos y Un Lado
Práctica: Triángulos ángulo-ángulo-lateral

