4.1.5: Ángulo Lateral - El Caso Ambiguo
- Page ID
- 107631
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Evaluar triángulos dados dos lados y un ángulo no entre ellos
Posibles triángulos con ángulo lateral
Tu equipo acaba de ganar la bandera en un torneo de futbol de bandera en tu escuela. Como recompensa, puedes llevarte a casa la bandera y guardarla hasta el próximo juego, cuando el otro equipo intentará recuperarla. La bandera se ve así:
Hace un triángulo isósceles. Empiezas a preguntarte cuántos triángulos posibles diferentes hay para diferentes longitudes de lados. Por ejemplo, si haces un triángulo oblicuo que tiene un ángulo dado mayor a noventa grados, ¿cuántas formas hay de hacer esto? ¿Se puede determinar cuántos triángulos posibles diferentes hay si el triángulo es un triángulo isósceles?
Triángulos SSA
En Geometría aprendiste que dos lados y un ángulo no incluido no necesariamente definen un triángulo único.
Considerar los siguientes casos dados\(a\),\(b\) y\(\angle A\):
Caso 1: No existe ningún triángulo (\(a<b\))
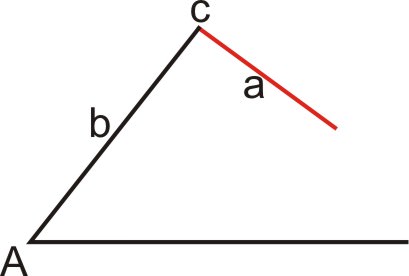
En este caso\(a<b\) y lado\(a\) es demasiado corto para llegar a la base del triángulo. Como no existe ningún triángulo, no hay solución.
Caso 2: Existe un triángulo (\(a<b\))
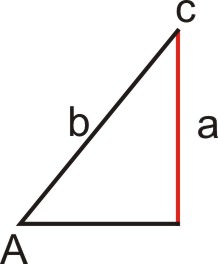
En este caso,\(a<b\) y lado\(a\) es perpendicular a la base del triángulo. Dado que esta situación arroja exactamente un triángulo, hay exactamente una solución.
Caso 3: Existen dos triángulos (\(a<b\))
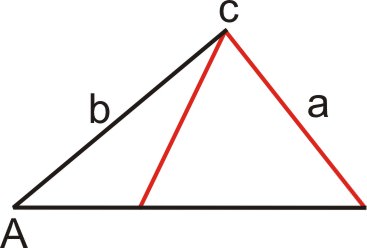
En este caso,\(a<b\) y lateral\(a\) se encuentra con la base exactamente en dos puntos. Dado que existen dos triángulos, hay dos soluciones.
Caso 4: Existe un triángulo (\(a=b\))
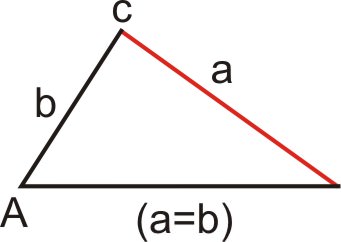
En este caso\(a=b\) y lado\(a\) se encuentra con la base exactamente en un punto. Como hay exactamente un triángulo, hay una solución.
Caso 5: Existe un triángulo (\(a>b\))
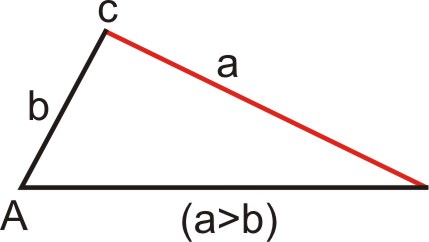
En este caso,\(a>b\) y el lado\(a\) se encuentra con la base exactamente en un punto. Como hay exactamente un triángulo, hay una solución.
El Caso 3 es referido como el Caso Ambiguo porque hay dos triángulos posibles y dos posibles soluciones. Una forma de verificar para ver cuántas soluciones posibles (si las hay) tendrá un triángulo es comparar lados\(a\) y\(b\). Si te enfrentas a la primera situación, dónde\(a<b\), aún podemos decir cuántas soluciones habrá mediante el uso de un y\(b\sin A\).
| Si: | Entonces: | |
|---|---|---|
| a. | \(a<b\) | Sin solución, una solución, dos soluciones |
| i. | \(a<b\sin A\) | Sin solución |
| ii. | \(a=b\sin A\) | Una solución |
| iii. | \(a>b\sin A\) | Dos soluciones |
| b. | \(a=b\) | Una solución |
| c. | \(a>b\) | Una solución |
Identificación de triángulos
Para los siguientes problemas, determine si los lados y ángulos dados determinan no, uno o dos triángulos.
1. El conjunto contiene un ángulo, su lado opuesto y el lado entre ellos.
\(a=5\),\(b=8\),\(A=62.19^{\circ}\)
\(5<8\),\(8 \sin62.19^{\circ} =7.076\). Entonces\(5<7.076\), lo que significa que no hay solución.
2. El conjunto contiene un ángulo, su lado opuesto y el lado entre ellos.
\(c=14\),\(b=10\),\(B=15.45^{\circ}\)
Aunque\(a\),\(b\) y no\(\angle A\) se usa en este ejemplo, siga el mismo patrón de la tabla multiplicando el lado no opuesto (del ángulo) por el ángulo.
\(10<14\),\(14\sin15.45^{\circ} =3.73\). Entonces\(10>3.73\), lo que significa que hay dos soluciones.
3. El conjunto contiene un ángulo, su lado opuesto y el lado entre ellos.
\(d=16\),\(g=11\),\(D=44.94^{\circ}\)
Aunque\(a\),\(b\) y no\(\angle A\) se usa en este ejemplo, siga el mismo patrón de la tabla multiplicando el lado no opuesto (del ángulo) por el ángulo.
\(16>11\), hay una solución.
Antes, te dieron un problema sobre un triángulo.
Solución
Como ya sabe, cuando se conocen dos lados de un triángulo con un lado incluido, y las longitudes de los dos lados son iguales, hay una posible solución. Dado que un triángulo isósceles cumple con estos criterios, solo hay una solución posible.
Determine cuántas soluciones habría para un triángulo en función de la información dada y calculándolo\(b \sin A\) y comparándolo con un. Dibuje un diagrama aproximado para cada problema en la casilla etiquetada como “diagrama”.
Solución
\(A=32.5^{\circ}\),\(a=26\),\(b=37\)
\(A=32.5^{\circ}\),\(a=26\),\(b=37 \)
\(26>19.9 \)
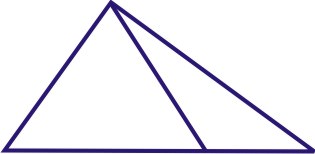
2 soluciones
Determine cuántas soluciones habría para un triángulo en función de la información dada y calculándolo\(b \sin A\) y comparándolo con un. Dibuje un diagrama aproximado para cada problema en la casilla etiquetada como “diagrama”.
Solución
\(A=42.3^{\circ}\),\(a=16\),\(b=26\)
\(A=42.3^{\circ}\),\(a=16\),\(b=26 \)
\(16<17.5\)
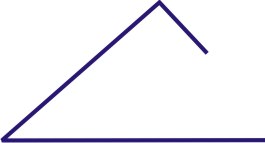
0 soluciones
Determine cuántas soluciones habría para un triángulo en función de la información dada y calculándolo\(b \sin A\) y comparándolo con un. Dibuje un diagrama aproximado para cada problema en la casilla etiquetada como “diagrama”.
Solución
\(A=47.8^{\circ}\),\(a=13.48\),\(b=18.2\)
\(A=47.8^{\circ}\),\(a=13.48\),\(b=18.2\)
\( 13.48=13.48 \)
1 solución
Revisar
Determinar si los lados y el ángulo dado determinan no, uno o dos triángulos. El conjunto contiene un ángulo, su lado opuesto y otro lado del triángulo.
- \(a=6\),\(b=6\),\(A=45^{\circ}\)
- \(a=4\),\(b=7\),\(A=115^{\circ}\)
- \(a=5\),\(b=2\),\(A=68^{\circ}\)
- \(a=7\),\(b=6\),\(A=34^{\circ}\)
- \(a=5\),\(b=3\),\(A=89^{\circ}\)
- \(a=4\),\(b=4\),\(A=123^{\circ}\)
- \(a=6\),\(b=8\),\(A=57^{\circ}\)
- \(a=4\),\(b=9\),\(A=24^{\circ}\)
- \(a=12\),\(b=11\),\(A=42^{\circ}\)
- \(a=15\),\(b=17\),\(A=96^{\circ}\)
- \(a=9\),\(b=10\),\(A=22^{\circ}\)
- En\(\Delta ABC\),\(a=4\),\(b=5\), y\(m\angle A=32^{\circ}\). Encuentra el valor (s) posible (es) de\(c\).
- En\(\Delta DEF\),\(d=7\),\(e=5\), y\(m\angle D=67^{\circ}\). Encuentra el valor (s) posible (es) de\(f\).
- En\(\Delta KQD\),\(m\angle K=20^{\circ}\),\(k=24\), y\(d=31\). Encuentra\(m\angle D\).
- En\(\Delta MRS\),\(m\angle M=70^{\circ}\),\(m=44\), y\(r=25\). Encuentra\(m\angle R\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.9.
vocabulario
| Término | Definición |
|---|---|
| Triángulo lateral lateral | Un triángulo de ángulo lateral es un triángulo donde la longitud de dos lados y uno de los ángulos que no está entre los dos lados son cantidades conocidas. |
Recursos adicionales
Video: Determinar la cantidad de triángulos resultantes de un triángulo SSA
Práctica: Ángulo lateral: el caso ambiguo