4.1.7: Problemas de Trigonometría
- Page ID
- 107639
Uso contextual de propiedades triangulares, ratios, teoremas y leyes.
Ángulo de depresión y ángulo de elevación
Una aplicación de las relaciones trigonométricas es encontrar longitudes que no se puedan medir. Muy frecuentemente, los ángulos de depresión y elevación se utilizan en este tipo de problemas.
Ángulo de Depresión: El ángulo medido hacia abajo desde el horizonte o una línea horizontal.

Ángulo de elevación: El ángulo medido desde el horizonte o una línea horizontal.

¿Y si colocas una escalera a 10 pies de un heno cuyo piso está a 20 pies del suelo? ¿Qué tan alta tendría que ser la escalera para llegar al piso del heno si forma un\(30^{\circ}\) ángulo con el suelo?
Un estudiante de matemáticas está parado a 25 pies de la base del Monumento a Washington. El ángulo de elevación desde su línea de visión horizontal es\(87.4^{\circ}\). Si su “altura de ojos” es de 5 pies, ¿qué tan alto es el monumento?

Solución
Podemos encontrar la altura del monumento usando la relación tangente.
\(\begin{aligned} \tan 87.4^{\circ} &=\dfrac{h}{25} \\ h&=25\cdot \tan 87.4^{\circ}=550.54 \end{aligned}\)
Añadiendo 5 pies, la altura total del Monumento a Washington es de 555.54 pies.
Un asta de bandera de 25 pies de altura proyecta una sombra de 42 pies. ¿Cuál es el ángulo que el sol golpea el asta de la bandera?
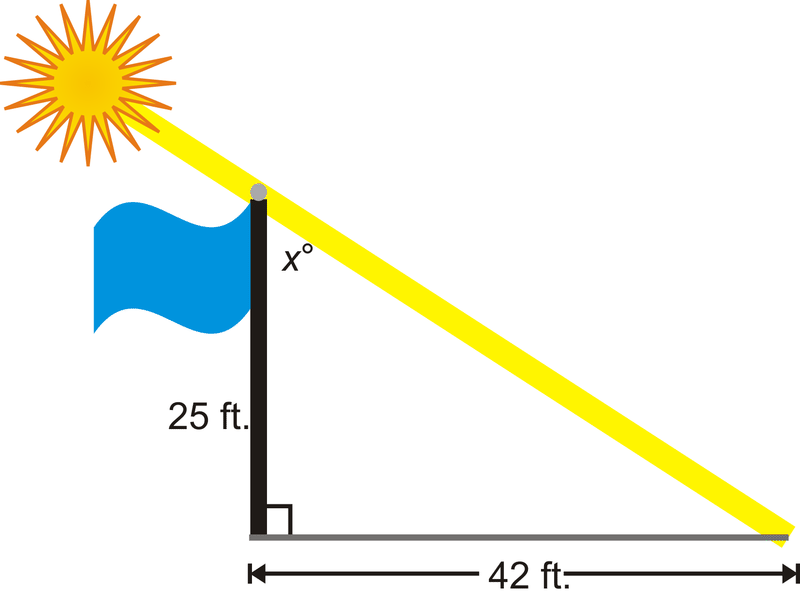
Solución
Dibuja un cuadro. El ángulo que el sol golpea el asta de la bandera es\(x^{\circ}\). Necesitamos usar la relación tangente inversa.
\(\begin{aligned} \tan x &=\dfrac{42}{25} \\ \tan^{−1} \dfrac{42}{25}&\approx 59.2^{\circ}=x \end{aligned}\)
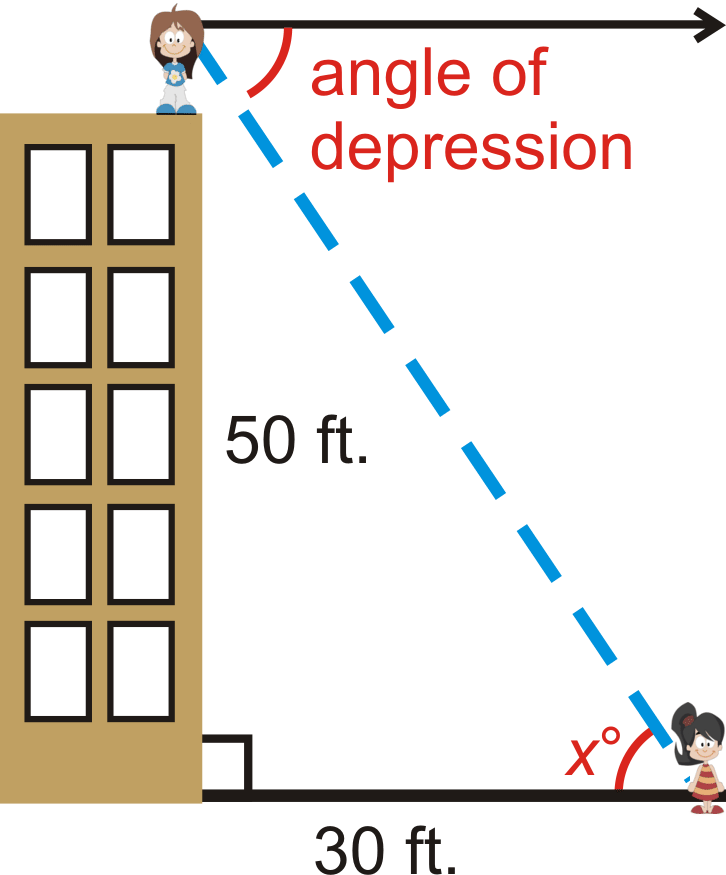
Elise está de pie en lo alto de un edificio de 50 pies y ve a su amiga, Molly. Si Molly está a 30 pies de distancia de la base del edificio, ¿cuál es el ángulo de depresión de Elise a Molly? La altura de los ojos de Elise es de 4.5 pies.
Solución
Debido a las líneas paralelas, el ángulo de depresión es igual al ángulo en Molly, o\(x^{\circ}\). Podemos usar la relación tangente inversa.
\(\tan^{−1} \left(\dfrac{54.5}{30}\right)=61.2^{\circ}=x\)
Mark está volando una cometa y se da cuenta de que 300 pies de cuerda están fuera. El ángulo de la cuerda con el suelo es\(42.5^{\circ}\). ¿Qué tan alto está la cometa de Mark sobre el suelo?
Solución
Podría ayudar a dibujar un cuadro. Después escribe y resuelve una ecuación trigonométrica.
\(\begin{aligned} \sin 42.5^{\circ} &=\dfrac{x}{300}\\ 300\cdot \sin 42.5^{\circ} &=x \\ x&\approx 202.7\end{aligned}\)
La cometa está a unos 202.7 pies del suelo.
Una escalera de 20 pies descansa contra una pared. La base de la escalera está a 7 pies de la pared. ¿Qué ángulo hace la escalera con el suelo?
Solución
Podría ayudar a dibujar un cuadro.
\(\begin{aligned} \cos x &=\dfrac{7}{20}\\ x&=\cos ^{−1}\dfrac{7}{20}\\ x&\approx 69.5^{\circ}\end{aligned}\)
Revisar
- Kristin está nadando en el océano y nota un arrecife de coral debajo de ella. El ángulo de depresión es\(35^{\circ}\) y la profundidad del océano, en ese punto es de 250 pies. ¿A qué distancia está ella del arrecife?
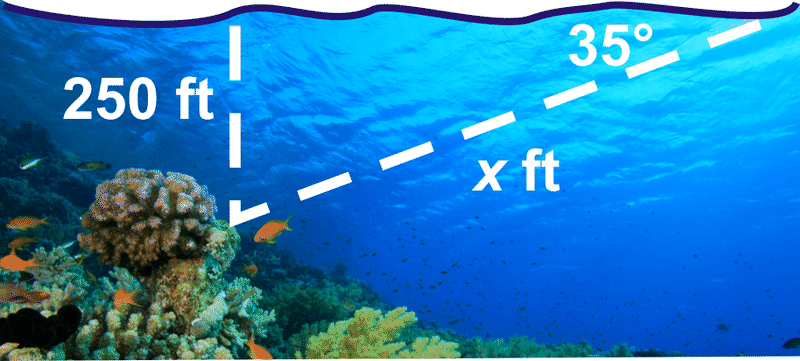
Figura\(\PageIndex{5}\) - La Torre Inclinada de Piza actualmente “se inclina” en\(4^{\circ}\) ángulo y tiene una altura vertical de 55.86 metros. ¿Qué altura tenía la torre cuando se construyó originalmente?

Figura\(\PageIndex{6}\)
Usa lo que sabes sobre los triángulos rectos para resolver el ángulo faltante. Si es necesario, dibuje un dibujo. Redondear todas las respuestas al décimo de grado más cercano.
- Un edificio de 75 pies proyecta una sombra de 82 pies. ¿Cuál es el ángulo que el sol golpea el edificio?
- A lo largo de 2 millas (horizontal), una carretera se eleva 300 pies (vertical). ¿Cuál es el ángulo de elevación?
- Un barco navega y ve un naufragio a 650 pies bajo el agua. Un buzo salta del bote y nada 935 pies para llegar al naufragio. ¿Cuál es el ángulo de depresión desde el barco hasta el naufragio?
- De pie a 100 pies de la base de un edificio, Sam mide el ángulo a la parte superior del edificio desde la altura de sus ojos para ser\(50^{\circ}\). Si sus ojos están a 6 pies sobre el suelo, ¿qué tan alto es el edificio?
- A lo largo de 4 millas (horizontal), una carretera se eleva 200 pies (vertical). ¿Cuál es el ángulo de elevación?
- Un edificio de 90 pies proyecta una sombra de 110 pies. ¿Cuál es el ángulo que el sol golpea el edificio?
- Luke está volando una cometa y se da cuenta de que 400 pies de cuerda están fuera. El ángulo de la cuerda con el suelo es\(50^{\circ}\). ¿Qué tan alto está la cometa de Luke sobre el suelo?
- Una escalera de 18 pies descansa contra una pared. La base de la escalera está a 10 pies de la pared. ¿Qué ángulo hace la escalera con el suelo?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.9.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulo de depresión | El ángulo de depresión es el ángulo formado por una línea horizontal y la línea de visión hacia un objeto cuando la imagen de un objeto se encuentra debajo de la línea horizontal. |
| Ángulo de elevación | El ángulo de elevación es el ángulo formado por una línea horizontal y la línea de visión hasta un objeto cuando la imagen de un objeto se ubica por encima de la línea horizontal. |
| ASA | ASA, ángulo-lado-ángulo, se refiere a dos ángulos conocidos en un triángulo con un lado conocido entre los ángulos conocidos. |
| ley de cosenos | La ley de los cosenos es una norma que relaciona los lados de un triángulo con el coseno de uno de sus ángulos. La ley de los cosenos establece que C2=A2+B2−2ABCOSC, donde C es el ángulo a través del lado c. |
| ley de los senos | La ley de los senos es una regla aplicada a los triángulos que establece que la relación del seno de un ángulo al lado opuesto a ese ángulo es igual a la relación del seno de otro ángulo en el triángulo al lado opuesto a ese ángulo. |
| Tangente | La tangente de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud del lado adyacente al ángulo dado. |
| Relaciones trigonométricas | Ratios que nos ayudan a entender las relaciones entre lados y ángulos de triángulos rectos. |
Recursos adicionales
Video: Trigonometría Problemas de Palabras Principios - Básico
Actividades: Trigonometría Problemas de la Palabra Discusión Preguntas
Práctica: Trigonometría
Mundo real: Medir montañas

