4.1.8: Determinación de ángulos desconocidos usando la ley de cosenos
- Page ID
- 107605
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encontrar ángulo desconocido dado longitudes de los 3 lados
Sarine dibuja un triángulo. Mide la longitud de los costados y registra sus medidas de la siguiente manera. ¿Cuál es la medida\(C\) del ángulo del triángulo?
\(\begin{aligned} a&=3 \\ b&=4 \\ c&=5 \end{aligned}\)
Ley de Cosinos con SSS
La Ley de Cosinos,\(a^2+b^2−2ab\cos C\), se puede reorganizar para facilitar el cálculo de la medida del ángulo\(C\) cuando\(a\),\(b\) y\(c\) son todas las longitudes conocidas.
\(\begin{aligned} a^2+b^2−2ab \cos C &=c^2 \\ a^2+b^2−c^2 &=2ab\cos C\\ \dfrac{a^2+b^2−c^2}{2ab} &=\cos C \end{aligned}\)
que puede ser manipulado aún más para\(C=\cos ^{−1}\left(\dfrac{a^2+b^2−c^2 }{2ab}\right)\).
Encontremos la medida del ángulo más grande en el triángulo con longitudes laterales 12, 18 y 21.
Primero, debemos determinar qué ángulo será el más grande. Recordemos de Geometría que el lado más largo es opuesto al ángulo más grande. El lado más largo es 21 así que vamos a dejar\(c=21\) ya que\(C\) es el ángulo que estamos tratando de encontrar. Dejar\(a=12\)\(b=18\) y usar la fórmula para resolver\(C\) como se muestra. No importa a qué lados asignemos\(a\) y\(b\). Son intercambiables en la fórmula.
\(m\angle C=\cos ^{−1}\left(\dfrac{12^2+18^2−21^2 }{2(12)(18)}\right) \approx 86^{\circ}\)
Nota: Tenga cuidado de poner paréntesis alrededor de todo el numerador y todo el denominador en la calculadora para asegurar el orden correcto de las operaciones. La pantalla de tu calculadora debería verse así:
\(\cos ^{−1}((12^2+18^2−21^2)/(2(12)(18)))\)
Ahora vamos a encontrar el valor de\(x\), al grado más cercano.
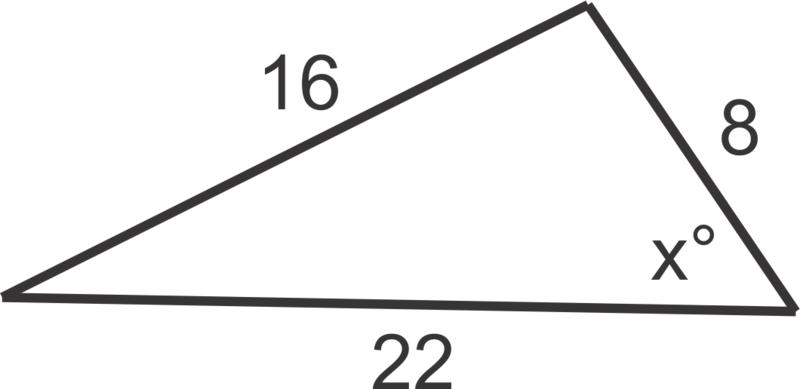
El ángulo con medida\(x^{\circ} \) será ángulo\(C\) así\(c=16\),\(a=22\) y\(b=8\). Recuerda,\(a\) y\(b\) son intercambiables en la fórmula. Ahora podemos sustituir las variables con las medidas conocidas y resolverlas.
\(\cos ^{−1}\left(\dfrac{22^2+8^2−16^2}{2(22)(8)}\right)\approx 34^{\circ}\)
Por último, encontremos el\(m\angle A\), si\(a=10\),\(b=15\) y\(c=21\).
Primero, reorganicemos la fórmula para reflejar los lados dados y el ángulo solicitado:
\(\cos A=\left(\dfrac{b^2+c^2−a^2}{2(b)(c)}\right)\), ahora enchufa nuestros valores
\(m\angle A=\cos ^{−1}\left( \dfrac{15^2+21^2−10^2}{2(15)(21)}\right) \approx 26^{\circ}\)
Anteriormente, se le pidió que encontrara la medida\(C\) del ángulo del triángulo que tiene lados\(a = 3\),\(b = 4\), y\(c = 5\).
Solución
Podemos usar la Ley manipulada de los Cosinos para resolver por\(C\).
\(\begin{aligned} C&=\cos ^{−1} \dfrac{3^2+4^2−5^2}{2(3)(4)} \\ C&=\cos ^{−1} \dfrac{9+16−25}{24} \\ C&=\cos ^{−1} \dfrac{0}{24}=\cos ^{−1} 0 \\ C&=90^{\circ} \end{aligned}\)
Por lo tanto, el triángulo es un triángulo rectángulo.
Encuentra la medida de\(x\) en el diagrama:
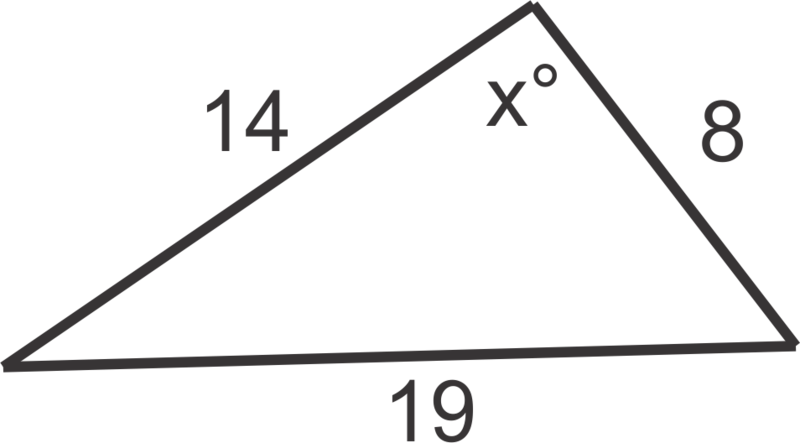
Solución
\(\cos ^{−1}\left(\dfrac{14^2+8^2−19^2}{2(14)(8)}\right) \approx 117^{\circ}\)
Encuentra la medida del ángulo más pequeño en el triángulo con longitudes laterales 47, 54 y 72.
Solución
El ángulo más pequeño será opuesto al lado con longitud 47, por lo que este será nuestro\(c\) en la ecuación.
\(\cos ^{−1}\left(\dfrac{54^2+72^2−47^2 }{2(54)(72)}\right) \approx 41^{\circ}\)
Encontrar\(m\angle B\), si\(a=68\),\(b=56\) y\(c=25\).
Solución
Reorganizar la fórmula para resolver\(m\angle B\),
\(\cos B=\left(\dfrac{a^2+c^2−b^2}{2(a)(c)}\right)\);\(\cos ^{−1}\left(\dfrac{68^2+25^2−56^2}{2(68)(25)}\right)\approx 52^{\circ}\)
Revisar
Utilizar la Ley de Cosinos para encontrar el valor de\(x\), al grado más cercano, en los problemas 1 a 6.
-
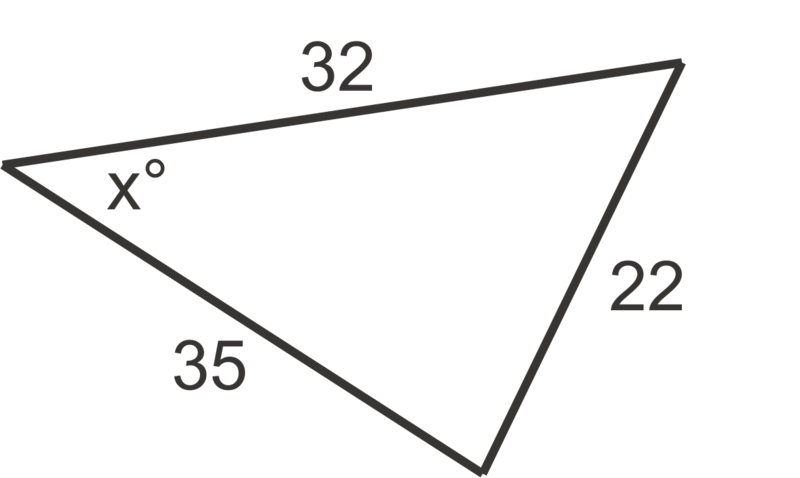
Figura\(\PageIndex{3}\) -
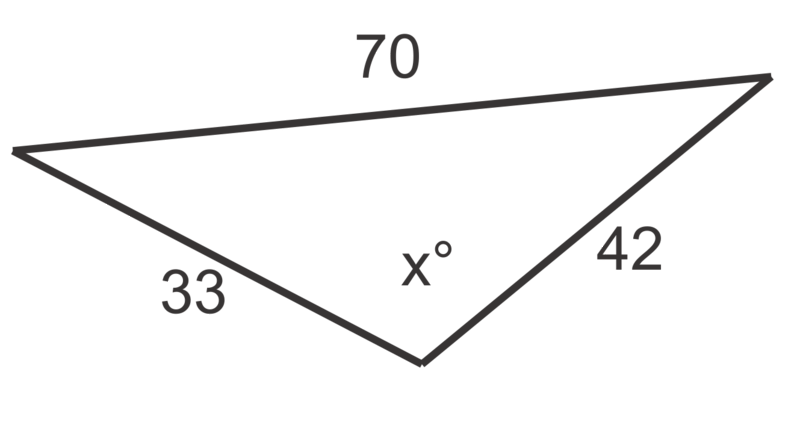
Figura\(\PageIndex{4}\) -
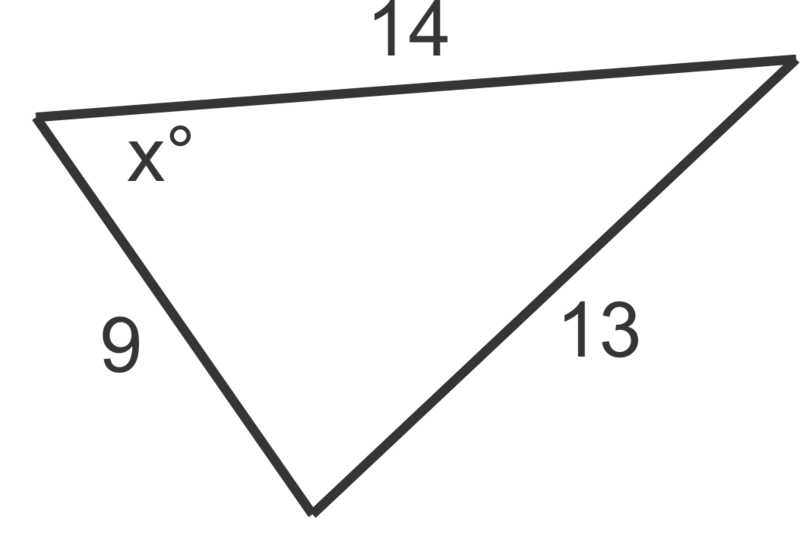
Figura\(\PageIndex{5}\) -
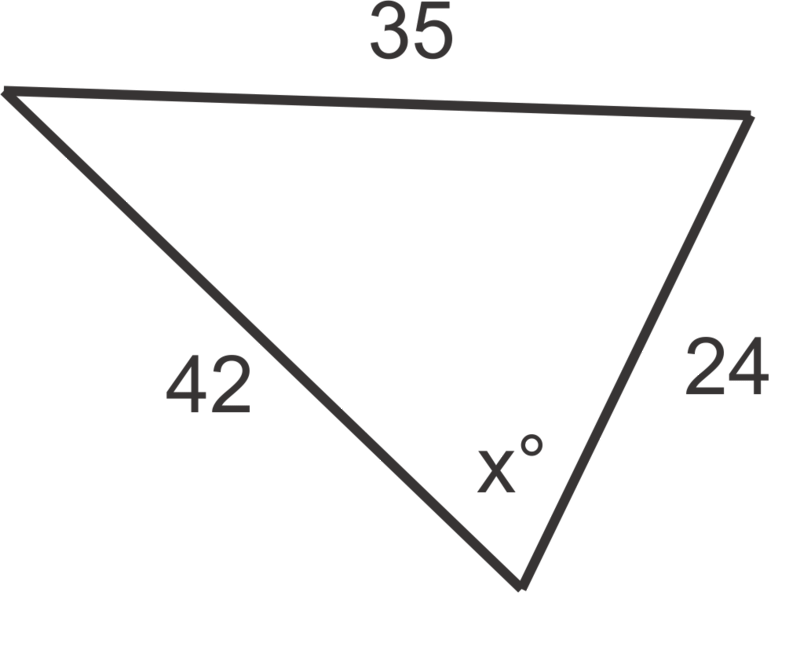
Figura\(\PageIndex{6}\) -
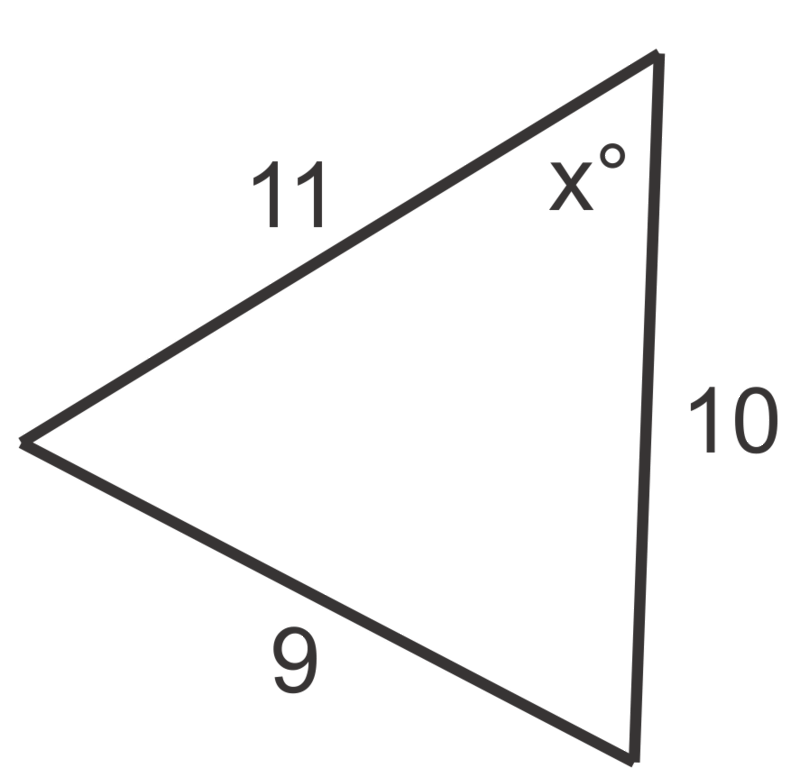
Figura\(\PageIndex{7}\) -
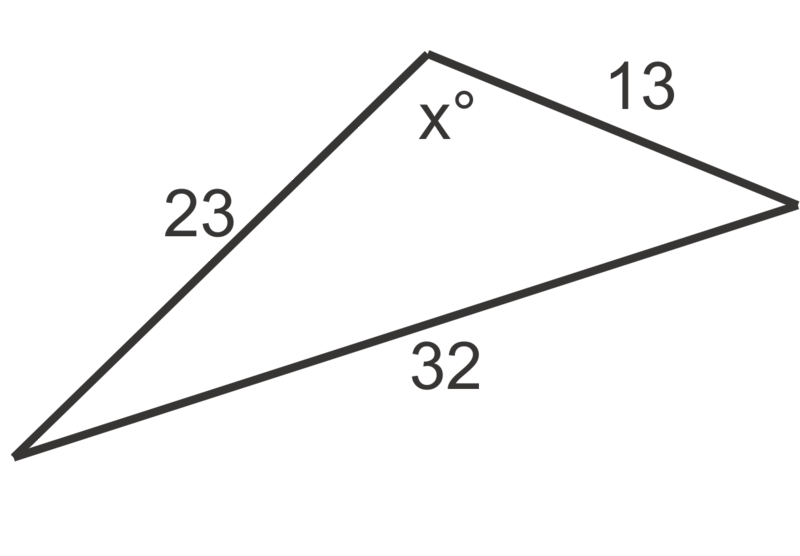
Figura\(\PageIndex{8}\) - Encuentra la medida del ángulo más pequeño en el triángulo con longitudes laterales de 150, 165 y 200 metros.
- Encuentra la medida del ángulo más grande en el triángulo con longitud lateral 59, 83 y 100 yardas.
- Encuentra el\(m\angle C\) si\(a=6\),\(b=9\) y\(c=13\).
- Encuentra el\(m\angle B\) si\(a=15\),\(b=8\) y\(c=9\).
- Encuentra el\(m\angle A\) si\(a=24\),\(b=20\) y\(c=14\).
- Un terreno triangular está bordeado por una carretera, una barda y un arroyo. Si el tramo a lo largo de la carretera es de 100 metros, la longitud de la barda es de 115 metros y el costado a lo largo del arroyo es de 90 metros, ¿en qué ángulo se encuentran la barda y la carretera?
Respuestas para problemas de revisión
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 13.16.
Recursos adicionales
Video: Ejemplo: Determinar la Medida de un Ángulo de un Triángulo Dada la Longitud de Tres Lados