5.1.3: Ecuaciones Polares Gráficas
- Page ID
- 107771
Puntos y gráficos basados en ecuaciones que involucran mediciones de radio y ángulo.
En el sistema de coordenadas rectangulares, los puntos se identifican por sus distancias desde los ejes x e y. En el sistema de coordenadas polares, los puntos se identifican por su ángulo en el círculo unitario y su distancia desde el origen. Se puede utilizar la trigonometría básica del triángulo rectángulo para traducir de un lado a otro entre las dos representaciones del mismo punto. ¿Cómo se ven afectadas las líneas y otras funciones por este nuevo sistema de coordenadas?
Coordenadas polares y rectangulares
Las coordenadas rectangulares son las\((x,y)\) coordenadas ordinarias a las que estás acostumbrado.
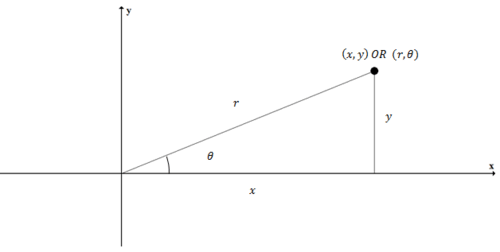
Las coordenadas polares representan el mismo punto, pero describen el punto por su distancia desde el origen (\(r\)) y su ángulo en el círculo unitario (\(\theta \)). Para traducir de ida y vuelta entre coordenadas polares y rectangulares se deben utilizar las relaciones trigonométricas básicas:
\ (\ comenzar {matriz} {l}
\ sin\ theta=\ dfrac {y} {r}\ fila derecha r\ cdot\ sin\ theta=y\
\ cos\ theta=\ dfrac {x} {r}\ fila derecha r\ cdot\ cos\ theta=x\
\ tan\ theta=\ dfrac {y} {x}\ fila derecha\ theta=\ tan ^ {-1}\ dfrac {y} {x}
\ end {array}\)
También se puede expresar la relación entre\(x\),\(y\) y\(r\) utilizando el Teorema de Pitágoras.
\(x^2+y^2=r^2\)
Tenga en cuenta que las coordenadas en forma polar no son únicas. Esto se debe a que hay un número infinito de ángulos coterminales que apuntan hacia cualquier\((x,\; y)\) coordenada dada.
Por ejemplo, el punto (3, 4) puede escribirse en coordenadas polares de al menos tres formas diferentes. Para encontrar\(\theta \), usa la tercera ecuación desde arriba y para encontrar r usa el teorema de pitágoras.
\ (\ begin {alineado}
\ tan\ theta&=\ dfrac {4} {3}\
\ theta&=\ tan ^ {-1}\ izquierda (\ dfrac {4} {3}\ derecha)\ aproximadamente 53.1^ {\ circ}\\
r^ {2} &=3^ {2} +4^ {2}\
r&=5
\ end {alineado}\)
Tres coordenadas polares equivalentes para el punto (3, 4) son:
\((5,53.1^{\circ} ),\;(5,413.1^{\circ} ),\;(−5,233.1^{\circ} )\)
Observe cómo la tercera coordenada apunta en la dirección opuesta y tiene un radio aparentemente negativo. Esto significa ir en la dirección opuesta al ángulo.
Una vez que puedas traducir de un lado a otro entre puntos, usa las mismas sustituciones para cambiar ecuaciones también. Se escribe una ecuación polar con el radio en función del ángulo. Esto significa que una ecuación en forma polar debe escribirse en la forma\(r=\underline{\qquad}\).
Para escribir una ecuación en forma polar, utilice las ecuaciones de conversión para sustituir. Por ejemplo, para convertir\(y=−x+1\) a forma polar hacer sustituciones para\(y\) y\(x\). Entonces, resuelve para\(r\).
\ (\ begin {alineado}
r\ cdot\ sin\ theta &=-r\ cdot\ cos\ theta+1\\
r\ cdot\ sin\ theta+r\ cdot\ cos\ theta &=1\\
r (\ sin\ theta+\ cos\ theta) &=1\\
r &=\ dfrac {1} {\ sin theta+\ cos\ theta\ eta}
\ final {alineado}\)
Anteriormente, se le preguntó cómo se pueden representar las líneas en el sistema de coordenadas polares.
Solución
La forma general de expresar una línea\(y=mx+b\) en forma polar es\(r=\dfrac{b}{\sin \theta −m\cdot cos\theta }\).
Expresar la siguiente ecuación usando coordenadas rectangulares:\(r=\dfrac{8}{1+2 \cos\theta }\).
Solución
Utilice el hecho de que\(r=\pm \sqrt{x^{2}+y^{2}}\) y\(r \cos\theta =x\)
\ (\ begin {alineado}
r+2 r\ cdot\ cos\ theta &=8\\
\ pm\ sqrt {x^ {2} +y^ {2}} +2 x &=8\
\ pm\ sqrt {x^ {2} +y^ {2}} &=8-2 x\\
x^ {2} +y^ {2} &=64-32 x+4 x^ {2}}\\
-3 x^ {2} +32 x+y^ {2} -64 &=0
\ final {alineado}\)
Esta es la ecuación de una hipérbola.
Esboce la siguiente ecuación polar:\(r=3\).
Solución
Dado que theta no está en la ecuación, puede variar libremente. Esta sencilla ecuación produce un círculo perfecto de radio 3 centrado en el origen.
Puedes demostrar que esta ecuación es equivalente a\(x^2+y^2=9\)
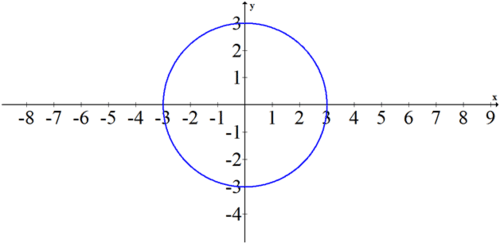
Esboce la siguiente ecuación polar:\(r=\theta \) con\(\theta :0\leq\theta \leq2\pi \).
Solución
La ecuación r=\ theta es un ejemplo de una ecuación polar que no se puede expresar fácilmente en forma rectangular. Para bosquejar la gráfica, identifique algunos puntos clave:\((0,0)\),\(\left(\dfrac{\pi}{2},\dfrac{\pi}{2}\right)\),\(\left(\pi ,\pi \right)\),\(\left(\dfrac{3 \pi}{2},\dfrac{3 \pi}{2}\right)\),\(\left(2\pi ,2\pi \right)\). Deberías ver que la forma es muy reconocible como una espiral.
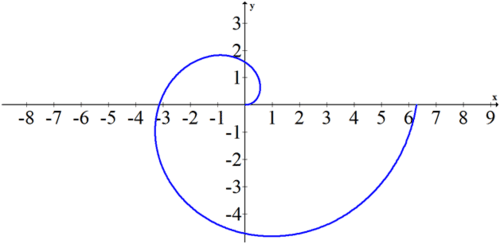
Traducir la siguiente expresión polar en coordenadas rectangulares y luego graficar.
\(r=2\cdot \sec \left(\theta −\dfrac{\pi }{2}\right)\)
Solución
Simplifique primero la ecuación polar antes de convertirla a coordenadas rectangulares.
\(\begin{aligned}r &=2\cdot \sec\left(\theta −\dfrac{\pi }{2}\right)\\ r\cdot \cos\left(\theta −\dfrac{\pi }{2}\right)&=2 \\ r\cdot cos(\dfrac{\pi}{2}−\theta ) &=2\\ r\cdot \sin \theta &=2\\ y&=2\end{aligned}\)
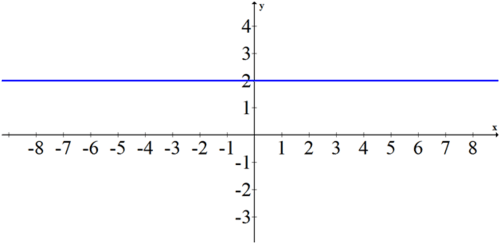
Revisar
Trazar las siguientes coordenadas polares.
1. \(\left(3, \dfrac{5\pi }{6}\right)\)
2. \(\left(2, \dfrac{\pi }{2}\right)\)
3. \(\left(4, \dfrac{−7\pi }{6}\right)\)
4. \(\left(−2, \dfrac{5\pi }{3}\right)\)
Dar dos conjuntos alternos de coordenadas para cada punto.
5. \((2,60^{\circ} )\)
6. \((5,330^{\circ} )\)
7. \((2,210^{\circ} )\)
Grafica cada ecuación.
8. \(r=4\)
9. \(\theta =\dfrac{\pi }{4}\)
10. \(r=2\theta \)con\(\theta : 0\leq\theta \leq2\pi \).
Convierte cada punto a forma rectangular.
11. \(\left(4, \dfrac{2\pi }{3}\right)\)
12. \(\left(3, \dfrac{\pi }{4}\right)\)
13. \((5, \dfrac{\pi }{3})\)
Convertir cada punto a forma polar usando radianes donde\(0\leq\theta <2\pi \).
14. (1, 3)
15. (1, -4)
16. (2, 6)
Convierte cada ecuación a forma polar.
17. \(x=3\)
18. \(2x+4y=2\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.1.
El vocabulario
| Término | Definición |
|---|---|
| Ángulos coterminales | Un conjunto de ángulos coterminales son ángulos con el mismo lado terminal pero expresados de manera diferente, como un número diferente de rotaciones completas alrededor del círculo unitario o ángulos que se expresan como mediciones de ángulo positivo versus negativo. |
| sistema de coordenadas polares | El sistema de coordenadas polares es un sistema de coordenadas especial en el que la ubicación de cada punto está determinada por su distancia desde el polo y su ángulo con respecto al eje polar. |
| coordenadas polares | Las coordenadas polares describen ubicaciones en una cuadrícula utilizando el sistema de coordenadas polares. La ubicación de cada punto está determinada por su distancia del polo y su ángulo con respecto al eje polar. |
| coordenadas rectangulares | Un punto se escribe usando coordenadas rectangulares si se escribe en términos de x e y y se puede graficar en el plano cartesiano. |
| círculo de unidad | El círculo unitario es un círculo de radio uno, centrado en el origen. |
Recursos adicionales
Video: Graficar ecuaciones polares - Descripción general
Práctica: Gráfica ecuaciones polares
Mundo Real: Escuchen

