5.2.1: Conversiones Polar y Rectangular
- Page ID
- 107746
Convertir de coordenadas polares a cartesianas.
Verás durante esta lección que los puntos se pueden convertir de forma rectangular a forma polar con un poco de álgebra y trigonometría.
¿Se puede convertir también la ecuación de una forma? ¿Qué tal un círculo, por ejemplo?
Transformación Polar y Cartesiana
Forma polar a forma rectangular
A veces se dará un problema con coordenadas en forma polar pero puede ser necesaria la forma rectangular.
Para transformar el punto polar\(\left(4,\dfrac{3\pi}{4}\right)\) en coordenadas rectangulares: primero identificar\((r, \theta )\).
\(r = 4\)y\(\theta =\dfrac{3\pi}{4}\).
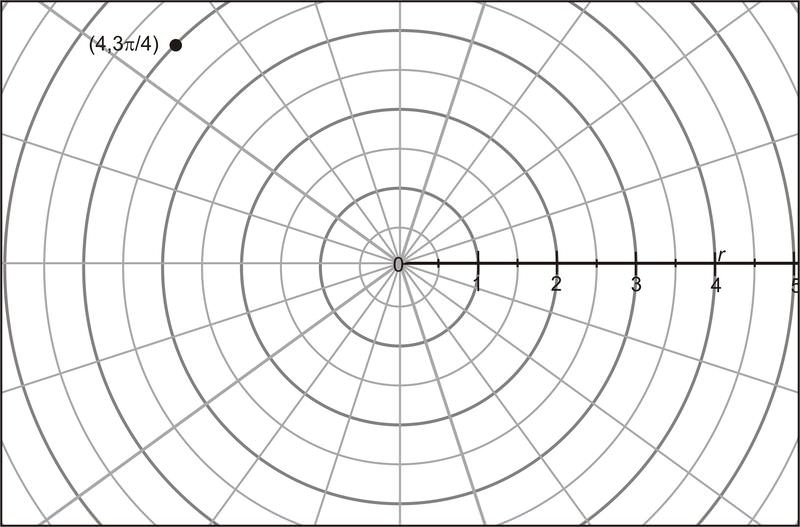
Segundo, dibuja una línea vertical desde el punto hasta el eje polar (el eje horizontal). La distancia desde el polo hasta donde la línea que acaba de dibujar cruza el eje polar es el valor x, y la longitud del segmento de línea desde el punto hasta el eje polar es el valor y.
Estas distancias se pueden calcular mediante trigonometría:
\(x = r \cos \theta\)y\(y = r \sin \theta\)
\(x=4 \cos \dfrac{3\pi}{4}\)y\(y=4 \sin \dfrac{3\pi}{4}\) o\(x=−2\sqrt{2} \)\(y=2\sqrt{2}\)
\(\left(4,\dfrac{3\pi}{4}\right)\)en coordenadas polares es equivalente a\((−2\sqrt{2} ,2\sqrt{2} )\) en coordenadas rectangulares.
Forma rectangular a forma polar
También es posible pasar de coordenadas rectangulares a coordenadas polares, pero se necesita un poco más de trabajo. Supongamos que queremos encontrar las coordenadas polares del punto rectangular (2,2). Para comenzar a realizar esta operación, la distancia que el punto (2,2) está desde el origen (el radio, r) se puede encontrar por
\ (\ begin {array} {l}
r=\ sqrt {x^ {2} +y^ {2}}\\
r=\ sqrt {2^ {2} +2^ {2}}\
r=\ sqrt {8} =2\ sqrt {2}
\ end {array}\)
El ángulo que el segmento de línea entre el punto y el origen se puede encontrar por
\ (\ begin {alineado}
\ tan\ theta&=\ dfrac {y} {x}\\
\ tan\ theta&=\ dfrac {2} {2}\\
\ tan\ theta&=1\\
\ theta&=\ tan ^ {-1} 1\\
\ theta&=\ dfrac {\ pi} {4}
\ end {alineado}\)
Dado que este punto está en el primer cuadrante (tanto la coordenada x como y son positivas) el ángulo debe ser\(45^{\circ}\) o\(\dfrac{\pi }{4}\) radianes. También es posible que cuando\(tan \theta = 1\) el ángulo pueda estar en el tercer cuadrante, o\(\dfrac{5\pi }{4}\) radianes. Pero este ángulo no va a satisfacer las condiciones del problema, ya que un ángulo de tercer cuadrante debe tener tanto x como y negativos.
Nota: al usar\(\tan \theta =\dfrac{y}{x}\) para encontrar la medida de\ theta se debe considerar, al principio, el cociente\(\tan \theta =\left| \dfrac{y}{x}\right|\) y encontrar el primer ángulo de cuadrante que satisfaga esta condición. Este ángulo se llamará el ángulo de referencia, denotado\(\theta_{ref}\). Encuentra el ángulo real analizando qué cuadrante se debe dar al ángulo los signos de x e y.
Anteriormente, se le preguntó si la ecuación de un círculo podría convertirse de forma rectangular a forma polar.
Solución
Ecuación de un círculo:\(x^2 + y^2 = k^2\) es la ecuación de un círculo con un radio de k en coordenadas rectangulares.
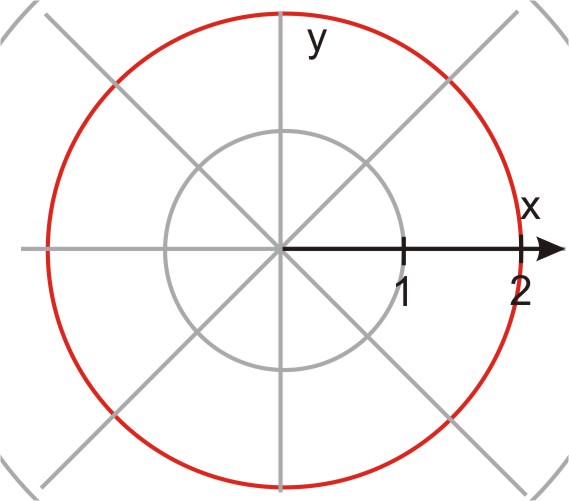
La ecuación de un círculo es extremadamente simple en forma polar. De hecho, ¡un círculo en una gráfica polar es análogo a una línea horizontal en una gráfica rectangular!
Puede transformar esta ecuación en forma polar sustituyendo los valores polares por x, y. Recordar\(x = r \cos \theta \) y\(y = r \sin \theta \).
\((r\cos \theta )^2 + (r \sin \theta )^2 = k^2\)
cuadrar los términos:\(r^2\cos^2 \theta + r^2\sin^2 \theta = k^2\),
factor el\(r^2\) de ambos términos a la izquierda:\(r^2(\cos^2 \theta + \sin^2 \theta ) = k^2\)
recordar la identidad:\(\cos^2 \theta + \sin^2 \theta = 1\)
\(r^2=k^2\)
Por lo tanto:\(r=\pm k\) es una ecuación para un círculo en unidades polares.
Cuando r es igual a una constante, la gráfica polar es un círculo.
Transformar las coordenadas polares\(\left(2,\dfrac{11 \pi}{6}\right)\) a forma rectangular.
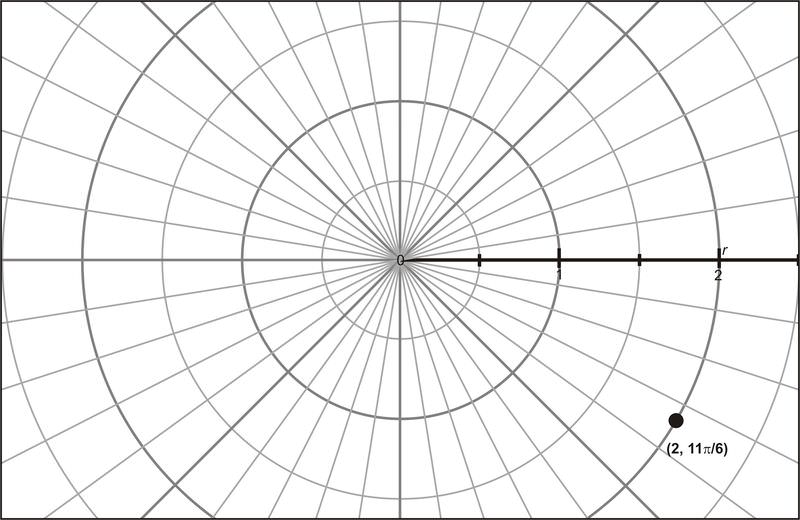
Solución
\(r=2\)y\(\theta =\dfrac{11 \pi}{6}\)
\(x=r \cos \theta \)y\(y=r \sin \theta\)
\(x=2 \cos \dfrac{11 \pi}{6}\)y\(y=2 \sin \dfrac{11 \pi}{6}\) o\(x=3\sqrt{2}\)\(y=−1\)
\(\left(2,\dfrac{11 \pi}{6}\right)\)es equivalente a\((3\sqrt{2} ,−1)\) o en forma decimal, aproximadamente\((4.342,−1)\).
Encuentra las coordenadas polares para\((3,−3\sqrt{3})\).
Solución
\(x=3\)y\(y=−3\sqrt{3}\)
Dibuja un triángulo rectángulo en forma estándar. Encuentra la distancia que el punto está desde el origen y el ángulo que el segmento de línea que representa esta distancia hace con el eje +x:
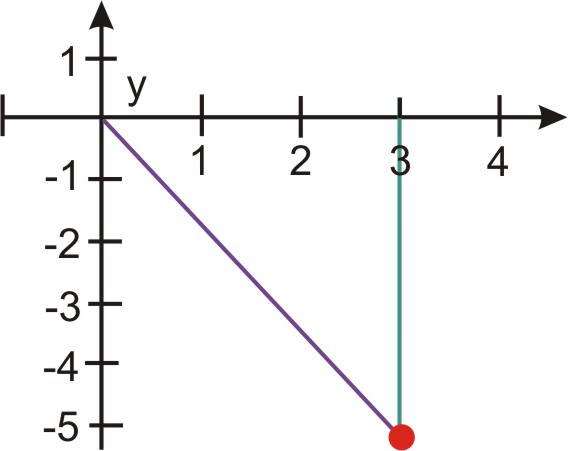
\(\begin{aligned} r&=\sqrt{3^2+(−3\sqrt{3})^2} \\ &=\sqrt{9+27} \\ &=\sqrt{36} \\ &=6 \end{aligned}\)
Y para el ángulo,
\(\begin{aligned}\tan \theta _{ref}&=\mid \dfrac{(−3\sqrt{3})}{3} \mid \\ \tan \theta _{ref}&=\sqrt{3} \\ \theta _{ref}&=\tan ^{−1} \sqrt{3} \\ \theta _{ref}&=\dfrac{\pi }{3}\end{aligned}\)
Entonces,\(\theta _{ref}=\dfrac{\pi }{3}\) y podemos mirar los signos de x e y — (+, -) — para ver eso\(\theta =\dfrac{5 \pi}{3}\) ya que es un ángulo de cuadrante 4º.
El punto rectangular\((3,−3\sqrt{3})\) es equivalente al punto polar\(\left(6,\dfrac{5 \pi}{3}\right)\).
Recordemos que al resolver para\(\theta \), usamos
\(\tan \theta =\mid \dfrac{(−3\sqrt{3})}{3} \mid\)o\(\tan \theta =\sqrt{3}\)
Encontramos\(\theta =\dfrac{5\pi }{3}\). PERO, también\(\theta\) podría ser\(\theta =\dfrac{2\pi }{3}\). Se deben examinar los signos de cada coordenada para ver que el ángulo debe estar en el cuarto cuadrante en unidades rectangulares o entre\(3\dfrac{\pi}{2}\) y\(2\pi\) en unidades polares. De los dos ángulos posibles para\(\theta \), sólo\(\dfrac{5\pi }{3}\) es válido. Tenga en cuenta que cuando usa tan -1 en una calculadora siempre obtendrá una respuesta en el rango\(−\dfrac{\pi}{2}\leq \theta \leq \dfrac{\pi}{2}\).
Convierte las siguientes coordenadas rectangulares en coordenadas polares.
- \((3,3\sqrt{3})\)
\((6,66^{\circ})\)
- \((−2,2)\)
\((2\sqrt{2} ,^225^{\circ})\)
Convierte las siguientes coordenadas polares en coordenadas rectangulares.
- \(\left(4,\dfrac{2\pi }{3}\right)\)
\((−2,^2\sqrt{3})\)
- \((−1, \dfrac{5\pi }{6})\)
\((\dfrac{\sqrt{3}}{2},−\dfrac{1}{2})\)
Expresar la ecuación en forma rectangular:\(r=6\cos \theta \).
Solución
\(r^2=6r\cos \theta \): multiplicar ambos lados por r
\(x^2+y^2=6x\): Uso\(x^2+y^2=r^2\) y\(x=r\cos \theta\)
\(\therefore x^2+y^2=6x\)es la ecuación en forma rectangular.
Expresar la ecuación en forma rectangular:\(r=6\).
Solución
Este es fácil:
\(r=6\)es la forma polar de la ecuación para un círculo
\(r^2=6^2\): cuadrado ambos lados
\(x^2+y^2=36 \): Usar\(x^2+y^2=r^2\) y simplificar
\(\therefore x^2+y^2=36\)es la ecuación en forma rectangular.
Revisar
- ¿Cómo se\((5,\pi )\) representa el punto con coordenadas polares en coordenadas rectangulares?
Trazar cada punto abajo en coordenadas polares\((r, \theta )\). Después escribe las coordenadas rectangulares\((x, y)\) para el punto.
- \((3,60^{\circ})\)
- \((−10, \dfrac{\pi }{3})\)
- \((15,\pi )\)
Se dan\((x, y)\) las coordenadas rectangulares. Para cada pregunta: a) Encuentra dos pares de coordenadas polares\((r, \theta )\), una con\(r > 0\) y la otra con\(r < 0\). b) Expresar\ theta en radianes, y redondear a la centésima más cercana.
- \((5,−5)\)
- \((0,10)\)
- \((−8,6)\)
Transforma cada ecuación polar en una ecuación usando coordenadas rectangulares. Identifique la gráfica y dé un boceto aproximado o una descripción del boceto.
- \(\theta =\dfrac{\pi }{10}\)
- \(r=8\)
- \(r\sin \theta =7\)
- \(r\cos \theta =−3\)
Transforma cada ecuación rectangular en una ecuación usando coordenadas polares. Identifique la gráfica y dé un boceto aproximado o una descripción del boceto.
- \(x^2+y^2−2x=0\)
- \(y=\sqrt{3}x\)
- \(y=−5\)
- \(xy=15\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.2.
El vocabulario
| Término | Definición |
|---|---|
| Tangente | La tangente de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud del lado adyacente al ángulo dado. |
| coseno | El coseno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud de la hipotenusa. |
| coordenadas polares | Las coordenadas polares describen ubicaciones en una cuadrícula utilizando el sistema de coordenadas polares. La ubicación de cada punto está determinada por su distancia del polo y su ángulo con respecto al eje polar. |
| forma polar | La forma polar de un punto o una curva se da en términos de r y\(\theta \) y se grafica en el plano polar. |
| cuadrante | Un cuadrante es un cuarto del plano de coordenadas. Los cuatro cuadrantes se numeran usando los números romanos I, II, III y IV, comenzando en la parte superior derecha y aumentando en sentido antihorario. |
| Cuadrantes | Un cuadrante es un cuarto del plano de coordenadas. Los cuatro cuadrantes se numeran usando los números romanos I, II, III y IV, comenzando en la parte superior derecha y aumentando en sentido antihorario. |
| coordenadas rectangulares | Un punto se escribe usando coordenadas rectangulares si se escribe en términos de x e y y se puede graficar en el plano cartesiano. |
| forma rectangular | La forma rectangular de un punto o una curva se da en términos de x e y y se grafica en el plano cartesiano. |
| seno | El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa. |

